Practice Questions: Percentages | CSAT Preparation - UPSC PDF Download
Q1: Candidates in a competitive examination consisted of 60% men and 40%women 70% men and 75% women cleared the qualifying test and entered the final test where 80% men and 70% women were successful.
Which of the following statements is correct?
(a) Success rate is higher for women
(b) Overall success rate is below 50%
(c) More men cleared the examination than women
(d) Both ‘a’ and ‘b’
Ans: (c)
Sol: Let there are 100 persons in which 60 men and 40 women.
Number of men who cleared the qualifying test
= 70 × 60/100 = 42
Number of women who cleared the qualifying test
= 40 × 3/4 = 30
Number of men who get success in final test
= 42 × 4/5 = 33.6
Number of women who get success in final test
= 30 × 70/100 = 21
Hence, more men cleared the examination than women.
Q2: In a town, 45% population read magazine A, 55% read magazine B, 40% read magazine C, 30% read magazines A and B, 15% read magazines B and C, 25% read magazines A and C; and 10% read all the three magazines. What percentage do not read any magazine?
(a) 10%
(b) 15%
(c) 20%
(d) 25%
Ans: (c)
Sol: Given,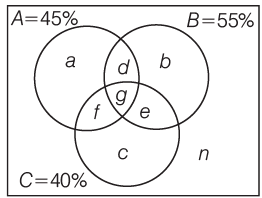
Given, d + g = 30% , e + g = 15%, f + g = 25% and g = 10%
∴ d = 20%, e = 5% and f = 15%
∴ a = A − (d + f + g ) = 0%
b = B − (d + e + g ) = 20%
c = C − (e + f + g ) = 10%
∴ Those who do not read any magazine
= Total population − (a + b + d + e + f + g ) = 20%
Q3: In a test, a candidate attempted only 8 questions and secured 50% marks in each of the quesitons. If he obtained a total of 40% in the test and all questions in the test carried equal marks, how many questions were there in the test?
(a) 8
(b) 10
(c) 15
(d) 16
Ans: (b)
Sol: Let the marks of each question be 10.
Then, total marks got by the candidate = 8 × 5 = 40 marks
40% = 40 ; 100% = 100
∴ Total number of questions = 100/10 = 10
Q4: A student attempted 24 questions and secured full marks in all of them. If he obtained 40% in the test and each question carried equal marks, then what was the total number of questions in the test?
(a) 30
(b) 40
(c) 60
(d) 70
Ans: (c)
Sol: Let the number of questions be x.
Then, x × 40% = 24 ⇒ x × 40/100 = 24
∴ x = 60
∴ Number of questions are 60.
Q5: A student is required to secure atleast 50% marks in order to pass an examination. He secured 50 marks which were less than the minimum passing marks by 50. The maximum marks of the paper are
(a) 200
(b) 250
(c) 275
(d) 300
Ans: (a)
Sol: Minimum passing marks = 50 + 50 = 100
Let the total marks be x.
Then, 50% of x = 100 ⇒ x = 100/50 × 100 = 200
∴ Total marks of paper are 200.
Q6: A city has a population of 300000 out of which 180000 are males. 50% of the population is literate. If 70% of the males are literate, then the number of literate females is
(a) 24000
(b) 30000
(c) 54000
(d) 60000
Ans: (a)
Sol: Total population = 300000
Total number of males = 180000
Total literates = 50% of total population = 150000
Number of literate males = 70% of males = 126000
∴ Number of literate females = 150000 − 126000 = 24000
Q7: 720 sweets were distributed equally amongst children in such a way that number of sweets received by each child is 20% of the total number of children. How many sweets did each receive?
(a) 12
(b) 14
(c) 11
(d) 15
Ans: (a)
Sol: Let total number of the children be x.
Then,
⇒ x2 = 5 × 720 = 5 × 5 × 144 ⇒ x = 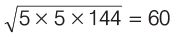
Number of sweets received by each child = 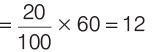
Q8: In an examination, every candidate took Physics or Mathematics or both. 65.8% took Physics and 59.2% took Mathematics. The total number of candidates was 2000. How many candidates took both Physics and Mathematics?
(a) 750
(b) 500
(c) 250
(d) 125
Ans: (b)
Sol: Let x % candidates take both the subjects.
∴ Percentage of candidates who opted Physics = 65.8% and percentage of candidates who opted Mathematics = 59.2%
∴ x = (65.8 + 59 . 2 − 100)% = (125 − 100)% = 25%
Also, total number of candidates = 2000
∴ Number of candidates who opted both the subjects = 25/100 × 2000 = 500
Q9: A farmer is increasing the length of his rectangular field by 25% and reducing its breadth by 15% due to soil problem. What will be the percentage change in the area of the plot?
(a) 40%
(b) 10%
(c) 6 .25%
(d) 12.50%
Ans: (c)
Sol: Here, a = 25% and b = – 15
According to the formula,
Percentage change in area,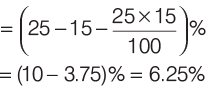
Q10: If the price of mangoes is decreased by 40%, one could get 32 more mangoes for ₹120, then find the original price of each mango.
(a) ₹ 3.50
(b) ₹ 2.50
(c) ₹ 2.25
(d) ₹ 2.00
Ans: (b)
Sol: Let the original price be ₹x per kg.
Then, new price per kg = 60% of x = 3x/5
According to the question,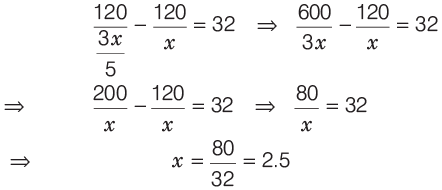
So, the original price is ₹ 2.50.
Q11: In a survey, it was found that 80% of those surveyed owned a car while 60% of those surveyed owned a mobile phone. If 55% owned both a car and a mobile phone, what per cent of those surveyed owned a car or a mobile phone or both?
(a) 65%
(b) 80%
(c) 85%
(d) 97.5%
Ans: (c)
Sol: Given that, percentage of car owners = 80%
Percentage of mobile phone owners = 60%
Percentage of people having both car and mobile phone = 55%
Percentage of people having only car = 80 − 55 = 25%
Percentage of people having only mobile phone = 60 − 55 = 5%
Percentage of people having a car or a mobile phone or both = 55% + 25% + 5% = 85%
Q12: A shopkeeper sells two tables at ₹ 1500 each. He earned a profit of 20% on one table and suffered a loss of 20% on the another table. Net profit or loss in this deal is
(a) 4% loss
(b) 4% profit
(c) 10% loss
(d) 10% profit
Ans: (a)
Sol: Here, a = 20 and b = – 20
∴ Profit or loss per cent,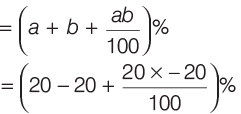
= − 4%
Thus, seller losses 4% in the deal.
Q13: The population of a city increases at the rate of 5% per annum. There is additional annual increase of 5% due to influx of job seekers. The per cent increase in population after 3 yr, is
(a) 33.1%
(b) 33%
(c) 34%
(d) 33.24%
Ans: (a)
Sol: Total increase in population per year = 5 + 5 = 10 %
According to the formula, Equivalent increase of 10%, 10% and 10% will be 
Here, a = 10%, b = 10% and c = 10%
Equivalent of a and b,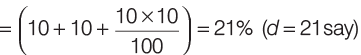
Now, equivalent of d and c 
Hence, the population increase after 3 yr is 33.1%.
Q14: A gardener increase the area of his rectangular garden by increasing its length by 40% and decreasing its width by 20%. The area of the new garden
(a) has increase by 20%
(b) has increase by 12%
(c) has increase by 8%
(d) is exactly the same as the old area
Ans: (b)
Sol: Let the length and breadth of garden be l and b, respectively.
∴ Area = l × b = lb
New length after 40% increase 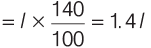
New breadth after 20% decrease = b × 80/100 = 0.8b
New area = 1.4 l × 0 .8 b = 1.12 lb
∴ Change in area percentage 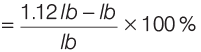
= 12% increase
(new area − original area = 0.12 > 0 i.e. increase)
Q15: The tank full of petrol in Arun’s motorcycle lasts for 10 days. If he starts using 25% more everyday, for how many days will the tank full of petrol last?
(a) 5 days
(b) 6 days
(c) 7 days
(d) 8 days
Ans: (d)
Sol: Let us assume that Arun uses x units of petrol everyday.
So, the amount of petrol in the tank when it is full will be 10 x.
If he started using 25% more petrol everyday, then the amount of petrol he now uses everyday will b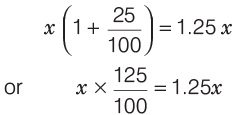
∴ Number of days his petrol will now last = Amount of petrol in tank/amount of petrol used everyday
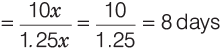
|
208 videos|138 docs|138 tests
|
FAQs on Practice Questions: Percentages - CSAT Preparation - UPSC
| 1. What is the basic formula for calculating percentages ? |  |
| 2. How can percentages be used in comparative analysis ? |  |
| 3. What is the relationship between percentage change and absolute change ? |  |
| 4. How do you convert a fraction to a percentage ? |  |
| 5. What are some common mistakes to avoid when calculating percentages ? |  |

|
Explore Courses for UPSC exam
|

|
















