Probability: Solved Examples - 1 | CSAT Preparation - UPSC PDF Download
Q1: Find the probability that a vowel selected at random from the 5 vowels is an ‘i’.
(a) 4/5
(b) 1/3
(c) 1/5
(d) 1/2
Ans: (c)
Sol: Here, n(S ) = {a, e, i, o, u} = 5
and E = Event of selecting the vowel i = {i}
So, n(E) = 1
∴ 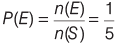
Q2: When three coins are tossed together, the probability that all coins have the same face up, is
(a) 1/3
(b) 1/6
(c) 1/8
(d) 1/12
Ans: (c)
Sol: Probability of head or a tail on upper side of a coin = 1/2
∴ Probability of getting same face on all three coins
= 1/2 × 1/2 × 1/2 = 1/8
Q3: Two unbiased dice are thrown simultaneously. The probability of getting the sum divisible by 3, is
(a) 11/36
(b) 1/3
(c) 13/36
(d) 17/36
Ans: (b)
Sol: Total number of events, n (S ) = 6 × 6 = 36
Number of ways of getting the sum divisible by 3,
n (E) = (1, 2 ),(2 , 1), (1, 5),(2 , 4),(3, 3) (4, 2),(5, 1),(3, 6),(4, 5) (5, 4),(6, 3),(6, 6) = 12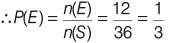
Q4: A and B aim a target. The probability that A hits the target is 5/7 and B hits the target is 7/10. What is the probability that exactly one of them hits the target?
(a) 21/10
(b) 29/70
(c) 31/70
(d) 33/70
Ans: (b)
Sol: Given, probability that A hits the target, P( A) = 5/7
So, probability that A do not hit the target,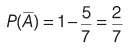
and probability that B hits the targets, P(B) = 7/10
So, probability that B do not hit the target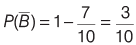
∴ Probability that exactly one of them hits the targets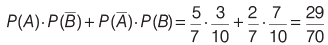
Q5: A speaks truth in 60% of the cases and B in 80% of the cases. In what percentage of cases are they likely to contradict each other, narrating the same incident?
(a) 70%
(b) 36%
(c) 22%
(d) 44%
Ans: (d)
Sol: Let A be the event that A speaks the truth and B be the event that B speaks the truth
Then,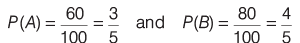
∴ 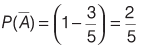
and 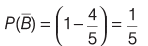
∴ P (A and B contradict each other)
= P [( A speaks the truth and B tells a lie) or ( A tells a lie and B speaks the truth)]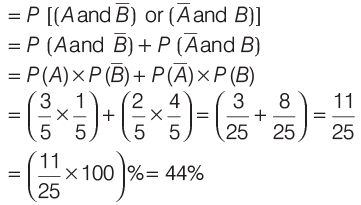
Q6: There are 8 blue and 4 white balls in a bag. A ball is drawn at random without replacing it, another ball is drawn. Then, find the probability that both the balls drawn are blue.
(a) 7/33
(b) 14/33
(c) 11/33
(d) 2/33
Ans: (b)
Sol: Total number of balls in the bag = 12
Probability of drawing one blue ball in the first draw,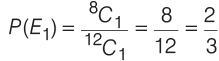
After the first draw of a blue ball, there are 7 blue and 4 white balls in the bag.
Then, total number of the balls in the bag is 11.
Probability of drawing one blue ball in the second draw,
∴ Probability that both are blue,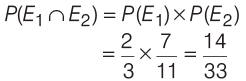
Q7: 100 students appeared for two examinations, 60 passed the first, 50 passed the second and 30 passed the both. The probability that a student selected at random has failed in both the examinations, is
(a) 0.3
(b) 0.2
(c) 0.4
(d) 0.1
Ans: (b)
Sol: 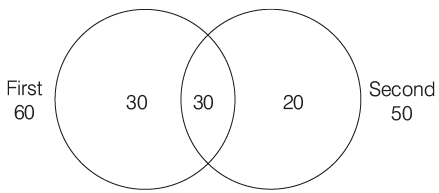
Total passed students = 30 + 30 + 20 = 80
Failed students = 100 − 80 = 20
∴ P (students failed in both exams) = 20/100 = 0.2
Q8: A complete cycle of a traffic light takes 60 s. During each cycle, the light is green for 25 s, yellow for 5 s and red for 30 s. At a randomly chosen time, the probability that the light will not be green, is
(a) 1/3
(b) 1/4
(c) 5/12
(d) 7/12
Ans: (d)
Sol: Time taken for complete cycle = 60 s
Probability that light will be green
∴ Probability that light will not be green = 1− 5/12 = 7/12
Q9: A student has 60% chance of passing in English and 54% chance of passing in both English and Mathematics. What is the per cent probability that he will fail in Mathematics?
(a) 12
(b) 36
(c) 4
(d) 10
Ans: (d)
Sol: Chance of passing in English = 60% = 0.6
Chance of passing in English and Mathematics = 54% = 0.54
Let chance of passing in Mathematics be x.
Since, passing in Mathematics and English are independent events, therefore,
Chance of passing in English and Mathematics = Chance of passing in English × Chance of passing in Mathematics
⇒ 0.54 = 0.6 × x ⇒ x = 0.9
∴ Chance of failing in Mathematics = 1 − 0.9 = 0.1
Probability% = 0.1 × 100 = 10%
Q10: Four different objects 1, 2, 3 and 4 are distributed at random in four places marked 1, 2, 3 and 4 . What is the probability that none of the objects occupy the place corresponding to its number?
(a) 17/24
(b) 3/8
(c) 1/2
(d) 5/8
Ans: (c)
Sol: Let the four places be
Now, object 1 cannot occupy the place 1.
Suppose object 2 occupies the place 
Then, other placements can be done in 6 ways as follows:
Here, out of six ways, only three are permissible, because (i), (iii) and (vi) are not permissible because of the non-fulfilment of Eq. (i).
Hence, the probability is = 3/6 = 1/2
Q11: From a pack of 52 playing cards, two cards are drawn together at random. Calculate the probability of both the cards being king.
(a) 1/15
(b) 25/57
(c) 35/256
(d) None of these
Ans: (d)
Sol: Two cards can be drawn from a pack of 52 playing cards in 52C2 ways.
i.e.
The event that two kings appear in a single draw of cards is 4C2 ways, i.e. 6 ways.
∴ Probability that the two cards drawn from a pack of 52 cards are kings = 6/1326 = 1/221
Q12: In a bag containing three balls, a white ball was placed and then one ball was taken out at random. What is the probability that the extracted ball would turn on to be white, if all possible hypothesis concerning the colour of the balls that were initially in the bag were equally possible?
(a) 5/8
(b) 3/4
(c) 1/2
(d) 3/8
Ans: (a)
Sol: Since, all possible hypothesis regarding the colour of the balls are equally likely, therefore these could be 3 white balls, initially in the bag.
∴ Required probability, 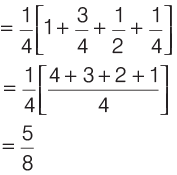
Q13: In his wardrobe, Girdhari has 3 trousers. One of them is grey, the second is blue and the third is brown. In his wardrobe, he also has 4 shirts. One of them is grey and the other 3 are white. He opens his wardrobe in the dark and picks out one shirt trouser pair without examining the colour. What is the probability that neither the shirt nor the trouser is grey?
(a) 1/12
(b) 1/6
(c) 1/4
(d) 1/2
Ans: (d)
Sol: Probability that trouser is grey = 1/3
Probability that trouser is not grey = 1 - 1/3 = 2/3
Probability that shirt is grey = 1/4
Probability that shirt is not grey = 1 - 1/4 = 3/4
∴ Required probability = 2/3 × 3/4 = 1/2
Q14: A bag contains 5 white, 7 red and 8 black balls. If 4 balls are drawn one by one with replacement, then what is the probability that all are white?
(a) 1/256
(b) 1/16
(c) 4/20
(d) 4/8
Ans: (a)
Sol: Number of white balls in the bag = 5
Total number of balls in the bag = 5 + 7 + 8 = 20
Probability that first ball drawn is white =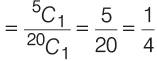
Since, balls are drawn with replacement, hence all the four events will have equal probability.
∴ Required probability 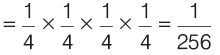
Q15: Two dice are thrown simultaneously. What is the probability of getting a number other than 4 on any dice?
(a) 25/36
(b) 1/3
(c) 17/36
(d) 2/3
Ans: (a)
Sol: Total number of events, n (S ) = 6 × 6 = 36
E = Event of getting a number other than 4 on any dice
n(E ) = {(1, 1),(1, 2 ),(1, 3),(1, 5),(1, 6),(2, 1),(2 , 2 ),(2, 3),(2, 5),
(2, 6),(3,1),(3,2 ),(3, 3),(3, 5),(3, 6),(5,1),(5,2 ),(5, 3) (5, 5),(5, 6), (6,1),(6,2 ),(6, 3),(6, 5),(6, 6)} = 25
|
208 videos|137 docs|138 tests
|
FAQs on Probability: Solved Examples - 1 - CSAT Preparation - UPSC
| 1. What is the importance of probability in the UPSC exam? |  |
| 2. How can I prepare for probability questions in the UPSC exam? |  |
| 3. What are some common types of probability problems asked in UPSC exams? |  |
| 4. Are there any specific formulas I should memorize for probability in the UPSC exam? |  |
| 5. How can I manage my time effectively while solving probability questions in the UPSC exam? |  |

|
Explore Courses for UPSC exam
|

|
















