Solved Examples: Ratio & Proportion | Mathematics for RRB NTPC / ASM - RRB NTPC/ASM/CA/TA PDF Download
Example 1: The ratio of the ages of Karthik and his son is 5 : 1. The present age of his son is 6 years. After how many years will the ratio of their ages be 7:3?
(a) 11
(b) 12
(c) 13
(d) 14
Ans: (b)
Let present age of karthik = 5k and his son = 1k
Given 1k = 6 ⇒5k = 30
Let x be the years after which their ages ratio becomes 7:3,
30 + x / 6 + x = 7/3
90 + 3x = 42 + 7x
48 = 4x
x = 48/4
x = 12
So the answer is option B.
Example 2: A, B, C started a business with capital ratio 4:2:3. Their period of investiments is in the ratio 3:5:4. Find their profit ratio ?
(a) 1:5:1
(b) 6:5:6
(c) 2:3:2
(d) 8:5:6
Ans: (b)
Ratio of their shares = (4 x 3):(2 x 5):(3 x 4) = 12:10:12 = 6:5:6
So the answer is option B.
Example 3: Sumeeth and Pranav started a business with initial investments of 3000/- and 5000/- respectively. After 8 months, Sumeeth left the business. The business made a profit of 490/- at the end of the year. What is the share of Pranav?
(a) 70
(b) 350
(c) 140
(d) 210
Ans: (b)
Sumeeth : pranav = (3000 x 8):(5000 x 120) = 24 : 60 = 2 :
Share of pranav = 5 / 2 + 5 x 490 = 5/7 x 490 = 350
So the answer is option B.
Example 4: Age of Ravi is
(a) 33
(b) 32
(c) 31
(d) 30
Ans: (c)
Age of Ravi = 4x , And age of his brother = 5x
Sum of their ages = 72
4x + 5x = 72
9x = 72
x = 8
Age of ravi’s brother before 9 years = 5 x -9 = 5(8) - 9 = 40 - 9 = 31
So the answer is option C.
Example 5: The ages of 5 persons are in AP. The youngest person was 31 years old while the oldest person was 39 years old. What is the average age of the 5 persons?
(a) 33
(b) 34
(c) 35
(d) 36
Ans: (c)
Given that their ages are in AP and least age is 31 and highest age is 39
1st term = a = 31
5th term = l = 39
Sum of their ages is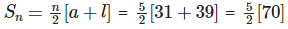
= 175
Hence average = 175 / 5
= 35
So the answer is option C.
Example 6: Suresh appeared for final exams of his class X. He scored an average of 50 marks in English, Hindi, Maths and Computers. His average score in Maths, Social Science, Science and Physical education was 70. If his average score in all 7 subjects was 58 then find his score in Maths.
(a) 68
(b) 74
(c) 72
(d) Cannot be determined
Ans: (b)
Let us assume that his scores in English be a, Hindi be b, Maths be c, computers be d, Social Science be e, Science be f and Physical Education be g. So we have
a + b + c + d = 50*4 = 200
Similarly,
c + e + f + g = 70*4 = 280
Adding both equations, we get
a + b + 2c + d + e + f + g = 480
We have been given that
a + b + c + d + e + f + g = 58*7 = 406
Subtracting both, we get c = 74
Hence, his marks in Maths must be 74.
Example 7: Two numbers are in the ratio 7 : 9. If 12 is subtracted from each, the new numbers we get are in the ratio 25 : 33. What is the difference of the 2 numbers?
(a) 56
(b) 32
(c) 44
(d) 38
Ans: (b)
Let the two numbers be 7x and 9x respectively
Also we have, 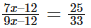
231x – 396 = 225x – 300
6x = 96
x = 16
So the two numbers are 112 and 144.
Required difference = 144 – 112 = 32
Hence, option B is the right choice.
Example 8: Eight years ago the age of the father was three times the age of the son. 4 years hence, their ages will be in the ratio 15:7. Find the present age of the father.
(a) 62
(b) 44
(c) 56
(d) 60
Ans: (c)
Let F, S are the present ages of father and son.
F - 8 = 3(S - 8)
3S - F = 16 -------(1)
F + 4 / S + 4 = 15 / 7
7F + 28 = 15S + 60
15S - 7F = -32 ------(2)
On solving (1) & (2)
15S - 5F = 80
15S - 7F = -32
we will get 2F = 112, F = 56
So the answer is option C.
Example 9: A shopkeeper has two varieties of rice. The cost price of the two varieties is Rs 40 per kg and Rs 54 per kg. The shopkeeper mixes the two varieties in a certain ratio and then sells the mixture at Rs 63 per kg. If the profit made by the shopkeeper is 40 % then find the ratio in which he mixed the two varieties of rice?
(a) 4:7
(b) 9:5
(c) 3:7
(d) 3:5
Ans: (b)
We know that by selling rice for Rupees 63 per kg, the shopkeeper makes a profit of 40 %. Hence, the cost price of the mixture for him will be 63/1.4 = 45 per kg. Let us say that he mixes ‘a’ kg of 40 rupees rice with ‘b’ kg of 54 rupees rice. Hence, we have
40*a + 54*b = 45(a + (b)
⇒ 40a + 54b = 45a + 45b
⇒ 5a = 9b
⇒ a/b = 9/5
Hence, the required ratio is 9:5
So the answer is option B.
Example 10: A shopkeeper has 2 varieties of rice. Rice A costs Rs.12/kg and Rice B costs Rs.15/Kg. The shopkeeper mixes the 2 varieties of rice in some ratio and sells the mixture at the cost price of rice B. He realizes a profit percentage of 12.5% by doing so. In what ratio did he mix the 2 rice varieties?
(a) 2:3
(b) 3:2
(c) 5:4
(d) 1:1
Ans: (c)
Let the quantity of rice A be ‘a’ and rice B be ‘b’.
(12a + 15(b)/(a + (b) is the cost price of a Kg of the mixed rice.
We know that the shopkeeper realizes a profit of 12.5% by selling it at Rs.15.
⇒ 1.125*(12a+15(b)/(a + (b) = 15
13.5a + 16.875b = 15a + 15b
1.5a = 1.875b
a/b = 1.875/1.5 = 5/4.
Hence, option C is the right answer.
Example 11: A student mixes 3 litres of pure river water with 4 litres of seawater. Seawater contains salt. If he able to retrieve 0.5 gms of salt per gram of the mixture, what is the amount of salt in sea water in grams per litre? The density of the final mixutre is .75 grams/ litre.
(a) 0.33 grams/ litre
(b) 0.44 grams/ litre
(c) 0.55 grams/ litre
(d) 0.66 grams/ litre
Ans: (d)
Total weight of water is 7 litres * 0.75 grams/litre = 5.25 grams
The amount of salt in the mixture = 5.25 * 0.5 = 2.63 grams.
So, the amount of salt in seawater = 2.63/4 = 0.66 grams/ litre
Example 12: Abdul and Waqar, together drink 2 litres of coconut water a day. If the quantity of coconut water consumed by Abdul is 30% more than Waqar, what is the difference between their water consumption quantity?
(a) 0.13 litres
(b) 0.26 litres
(c) 0.39 litres
(d) 0.52 litres
Ans: (b)
Let the amount consumed by Waqar be x litres
Amount consumed by Abdul = 1.3x
So, x + 1.3 x = 2 litres
2.3x = 2
So, x = 2/2.3 = 0.87
The required value = 1.3x – x = 0.3x = 0.3 * 0.87 = 0.26 litres
|
146 videos|96 docs|98 tests
|
FAQs on Solved Examples: Ratio & Proportion - Mathematics for RRB NTPC / ASM - RRB NTPC/ASM/CA/TA
| 1. What is the formula for calculating the ratio between two quantities? |  |
| 2. How can I simplify a ratio? |  |
| 3. What is the difference between ratio and proportion? |  |
| 4. How can I solve problems involving ratios in competitive exams? |  |
| 5. Can ratios be expressed in different forms? |  |
















