Class 8 Exam > Class 8 Notes > Mathematics (Maths) Class 8 > Mind Map: Rational Numbers
Mind Map: Rational Numbers | Mathematics (Maths) Class 8 PDF Download
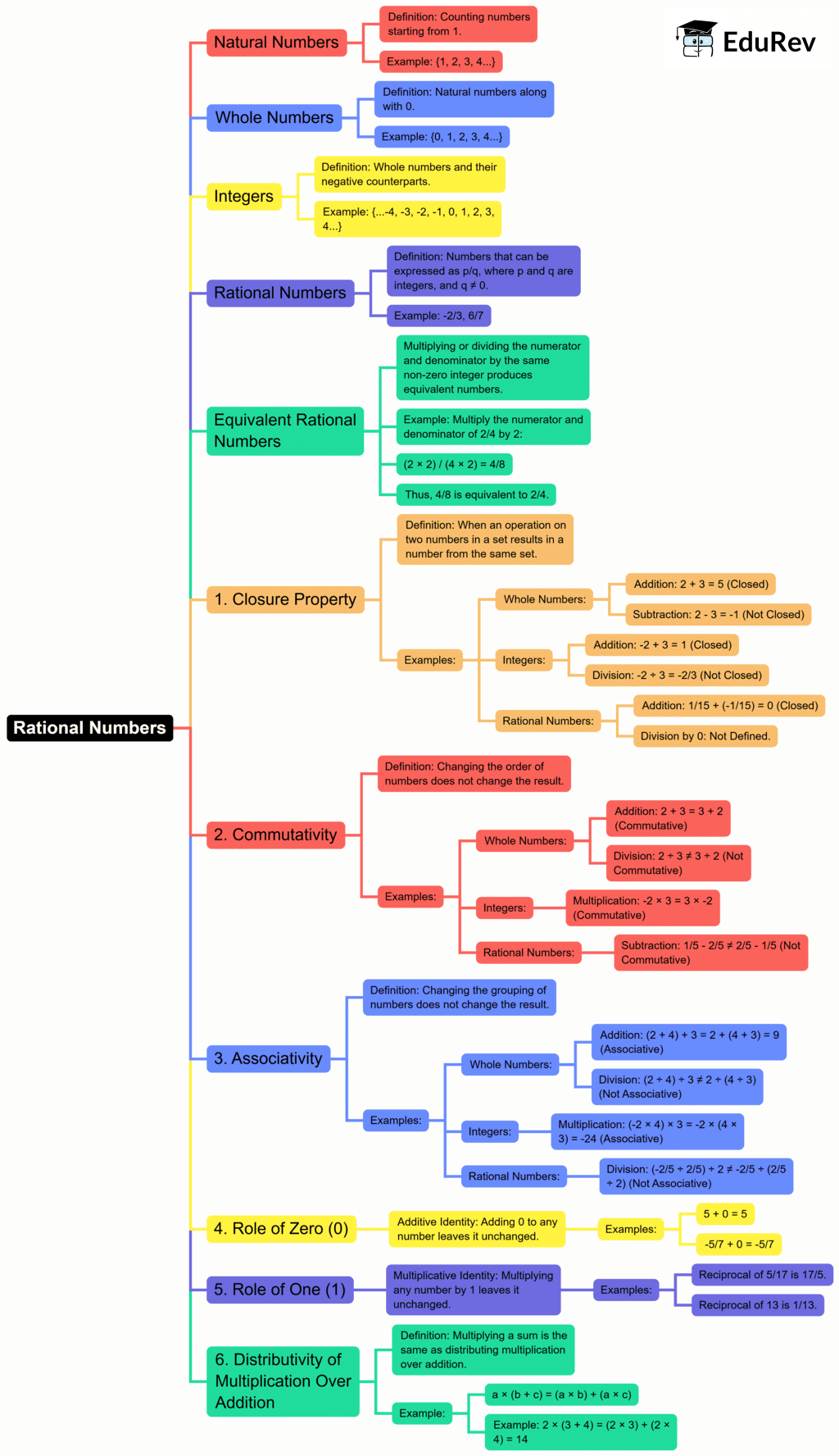
The document Mind Map: Rational Numbers | Mathematics (Maths) Class 8 is a part of the Class 8 Course Mathematics (Maths) Class 8.
All you need of Class 8 at this link: Class 8
|
81 videos|423 docs|31 tests
|
FAQs on Mind Map: Rational Numbers - Mathematics (Maths) Class 8
| 1. What are rational numbers, and how are they different from integers and whole numbers? |  |
Ans. Rational numbers are numbers that can be expressed as a fraction p/q, where p and q are integers, and q is not equal to zero. They include integers (which are whole numbers that can be positive, negative, or zero) as well as fractions. Whole numbers are a subset of rational numbers that include all non-negative integers (0, 1, 2, ...). Thus, while all integers and whole numbers are rational numbers, not all rational numbers are integers or whole numbers.
| 2. How do you convert a repeating decimal into a rational number? | |
Ans. To convert a repeating decimal into a rational number, let x be the repeating decimal. For example, if x = 0.666... (where 6 repeats), multiply both sides by 10 (to shift the decimal point) to get 10x = 6. Then, subtract the original equation from this new equation: 10x - x = 6, which simplifies to 9x = 6. Dividing both sides by 9 gives x = 6/9, which can be simplified to 2/3. Thus, 0.666... = 2/3 as a rational number.
| 3. What is the significance of the term "like" and "unlike" fractions in rational numbers? | |
Ans. "Like fractions" are fractions that have the same denominator, making them easy to compare and perform arithmetic operations like addition and subtraction. For example, 1/4 and 3/4 are like fractions. "Unlike fractions," on the other hand, have different denominators, which require finding a common denominator before performing operations. For instance, to add 1/3 and 1/4, you would first convert them to like fractions (common denominator of 12) to get 4/12 + 3/12 = 7/12.
| 4. How do you perform operations such as addition and subtraction on rational numbers? | |
Ans. To add or subtract rational numbers, first ensure they have a common denominator. For instance, to add 1/3 and 1/4, find a common denominator (12), converting the fractions to 4/12 and 3/12, respectively. Then, add the numerators: 4 + 3 = 7, resulting in 7/12. For subtraction, the process is the same, but you subtract the numerators instead. So, 5/6 - 1/3 would require converting 1/3 to 2/6, yielding 5/6 - 2/6 = 3/6, which simplifies to 1/2.
| 5. What are some real-life examples of rational numbers? | |
Ans. Rational numbers are prevalent in everyday life. For example, when measuring ingredients in cooking, such as 1/2 cup of sugar or 3/4 teaspoon of salt, these quantities are rational numbers. Similarly, when dealing with money, prices such as $4.50 or $2.75 represent rational numbers as they can be expressed as fractions (9/2 and 11/4, respectively). Additionally, in sports, scores and statistics often involve rational numbers, like a batting average of 0.250 or a completion percentage of 75/100.
About this Document
2.1K Views
4.90/5
Rating
Sep 23, 2025
Last updated
Document Description: Mind Map: Rational Numbers for Class 8 2025 is part of Mathematics (Maths) Class 8 preparation.
The notes and questions for Mind Map: Rational Numbers have been prepared according to the Class 8 exam syllabus. Information about Mind Map: Rational Numbers covers topics
like and Mind Map: Rational Numbers Example, for Class 8 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Mind Map: Rational Numbers.
Introduction of Mind Map: Rational Numbers in English is available as part of our Mathematics (Maths) Class 8
for Class 8 & Mind Map: Rational Numbers in Hindi for Mathematics (Maths) Class 8 course.
Download more important topics related with notes, lectures and mock test series for Class 8
Exam by signing up for free. Class 8: Mind Map: Rational Numbers | Mathematics (Maths) Class 8
Description
Full syllabus notes, lecture & questions for Mind Map: Rational Numbers | Mathematics (Maths) Class 8 - Class 8 | Plus excerises question with solution to help you revise complete syllabus for Mathematics (Maths) Class 8 | Best notes, free PDF download
Information about Mind Map: Rational Numbers
In this doc you can find the meaning of Mind Map: Rational Numbers defined & explained in the simplest way possible. Besides explaining types of
Mind Map: Rational Numbers theory, EduRev gives you an ample number of questions to practice Mind Map: Rational Numbers tests, examples and also practice Class 8
tests
Related Searches
video lectures
,mock tests for examination
,Free
,Viva Questions
,shortcuts and tricks
,ppt
,Mind Map: Rational Numbers | Mathematics (Maths) Class 8
,practice quizzes
,Mind Map: Rational Numbers | Mathematics (Maths) Class 8
,study material
,Mind Map: Rational Numbers | Mathematics (Maths) Class 8
,Extra Questions
,Summary
,Important questions
,Semester Notes
,Exam
,Sample Paper
,Objective type Questions
,MCQs
,past year papers
,Previous Year Questions with Solutions
;
Additional Information about Mind Map: Rational Numbers for Class 8 Preparation
Mind Map: Rational Numbers Free PDF Download
The Mind Map: Rational Numbers is an invaluable resource that delves deep into the core of the Class 8 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Mind Map: Rational Numbers now and kickstart your journey towards success in the Class 8 exam.
Importance of Mind Map: Rational Numbers
The importance of Mind Map: Rational Numbers cannot be overstated, especially for Class 8 aspirants.
This document holds the key to success in the Class 8 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Mind Map: Rational Numbers Notes
Mind Map: Rational Numbers Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Mind Map: Rational Numbers.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Mind Map: Rational Numbers Notes on EduRev are your ultimate resource for success.
Mind Map: Rational Numbers Class 8 Questions
The "Mind Map: Rational Numbers Class 8 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 8 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Mind Map: Rational Numbers on the App
Students of Class 8 can study Mind Map: Rational Numbers alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Mind Map: Rational Numbers,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Mind Map: Rational Numbers is prepared as per the latest Class 8 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup