Mind Map: Linear Algebra
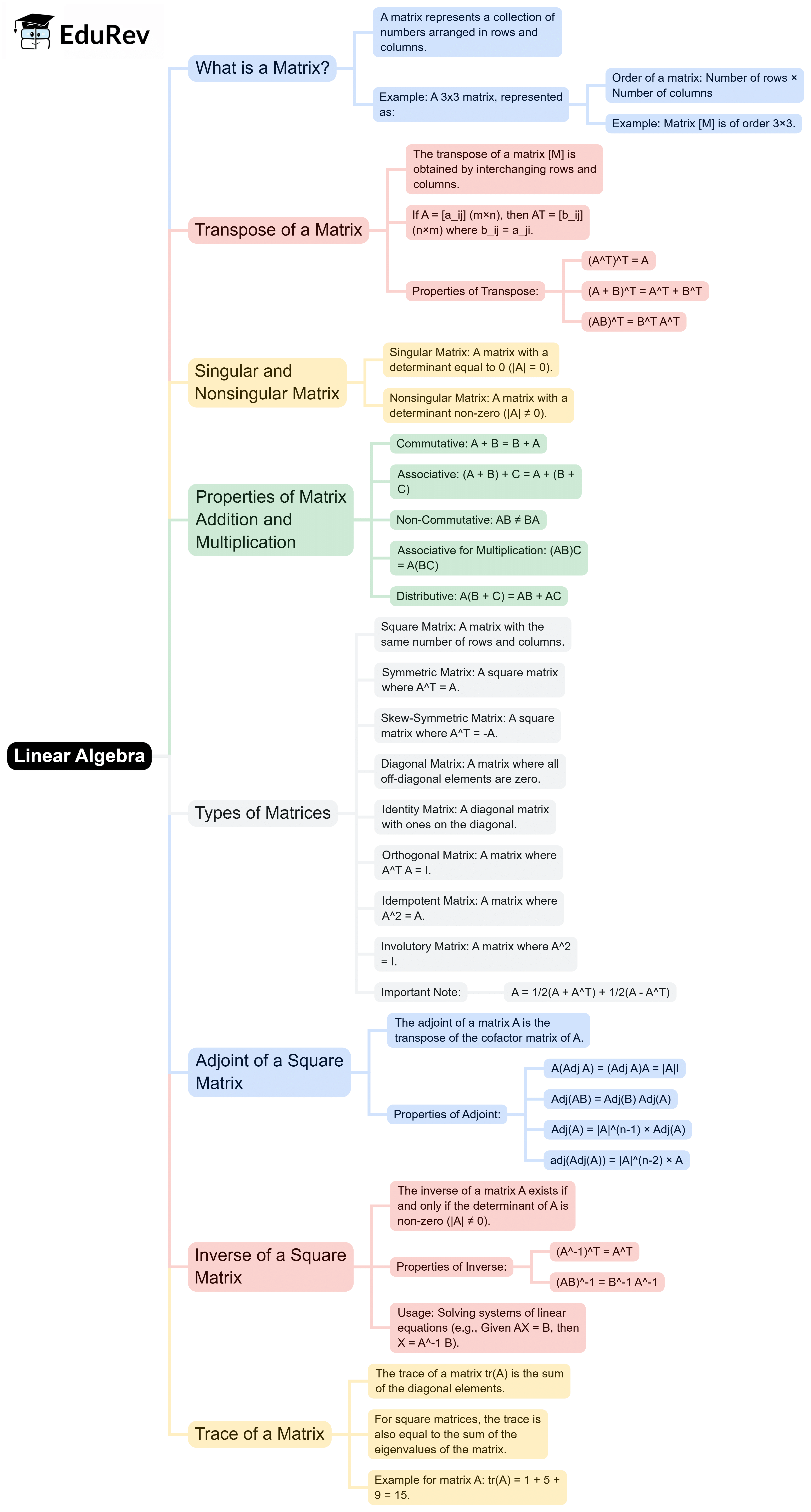
The document Mind Map: Linear Algebra is a part of the Computer Science Engineering (CSE) Course Engineering Mathematics for Computer Science Engineering.
All you need of Computer Science Engineering (CSE) at this link: Computer Science Engineering (CSE)
FAQs on Mind Map: Linear Algebra
| 1. What are the key concepts of linear algebra that are essential for computer science engineering? |  |
Ans. Key concepts include vector spaces, matrices, determinants, eigenvalues and eigenvectors, and linear transformations. Understanding these concepts is crucial for solving problems in graphics, machine learning, and data analysis.
| 2. How is linear algebra applied in machine learning? | |
Ans. Linear algebra is fundamental in machine learning for data representation, optimization algorithms, and model training. Concepts like matrices and vectors are used to represent datasets, while operations like matrix multiplication help in transforming and reducing dimensions of data.
| 3. What role do matrices play in computer graphics? | |
Ans. In computer graphics, matrices are used to perform transformations such as translation, rotation, and scaling of objects. They allow for efficient manipulation of image data and are essential for rendering scenes in 2D and 3D graphics.
| 4. Why is it important to understand eigenvalues and eigenvectors in CSE? | |
Ans. Eigenvalues and eigenvectors are important for dimensionality reduction techniques like Principal Component Analysis (PCA), which is widely used in data compression, feature extraction, and machine learning models. They help identify the directions of maximum variance in data.
| 5. How can I improve my understanding of linear algebra for computer science applications? | |
Ans. To improve understanding, one can practice solving linear algebra problems, take online courses specifically tailored for computer science applications, and engage in projects that utilize linear algebra concepts, such as implementing algorithms in machine learning or graphics.
About this Document
4.92/5 Rating
Apr 18, 2026 Last updated
Related Exams
Document Description: Mind Map: Linear Algebra for Computer Science Engineering (CSE) 2026 is part of Engineering Mathematics for Computer Science Engineering preparation. The notes and questions for Mind Map: Linear Algebra have been prepared according to the Computer Science Engineering (CSE) exam syllabus. Information about Mind Map: Linear Algebra covers topics like and Mind Map: Linear Algebra Example, for Computer Science Engineering (CSE) 2026 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Mind Map: Linear Algebra.
Introduction of Mind Map: Linear Algebra in English is available as part of our Engineering Mathematics for Computer Science Engineering for Computer Science Engineering (CSE) & Mind Map: Linear Algebra in Hindi for Engineering Mathematics for Computer Science Engineering course. Download more important topics related with notes, lectures and mock test series for Computer Science Engineering (CSE) Exam by signing up for free. Computer Science Engineering (CSE): Mind Map: Linear Algebra
Description
Mind Map: Linear Algebra of Engineering Mathematics provides you one-page visual summary of the chapter covering all the important topics. Download the PDF from EduRev.
Information about Mind Map: Linear Algebra
In this doc you can find the meaning of Mind Map: Linear Algebra defined & explained in the simplest way possible. Besides explaining types of Mind Map: Linear Algebra theory, EduRev gives you an ample number of questions to practice Mind Map: Linear Algebra tests, examples and also practice Computer Science Engineering (CSE) tests
 | Explore Courses for Computer Science Engineering (CSE) exam |  |
 | Get EduRev Notes directly in your Google search | |
Related Searches
Viva Questions, Previous Year Questions with Solutions, MCQs, mock tests for examination, practice quizzes, shortcuts and tricks, pdf , Extra Questions, Sample Paper, past year papers, ppt, Mind Map: Linear Algebra, Free, Semester Notes, video lectures, Important questions, Mind Map: Linear Algebra, Exam, Mind Map: Linear Algebra, Objective type Questions, study material, Summary;