Engineering Mathematics Exam > Engineering Mathematics Notes > Engineering Mathematics > Mind Map: Differential Equations
Mind Map: Differential Equations | Engineering Mathematics - Engineering Mathematics PDF Download
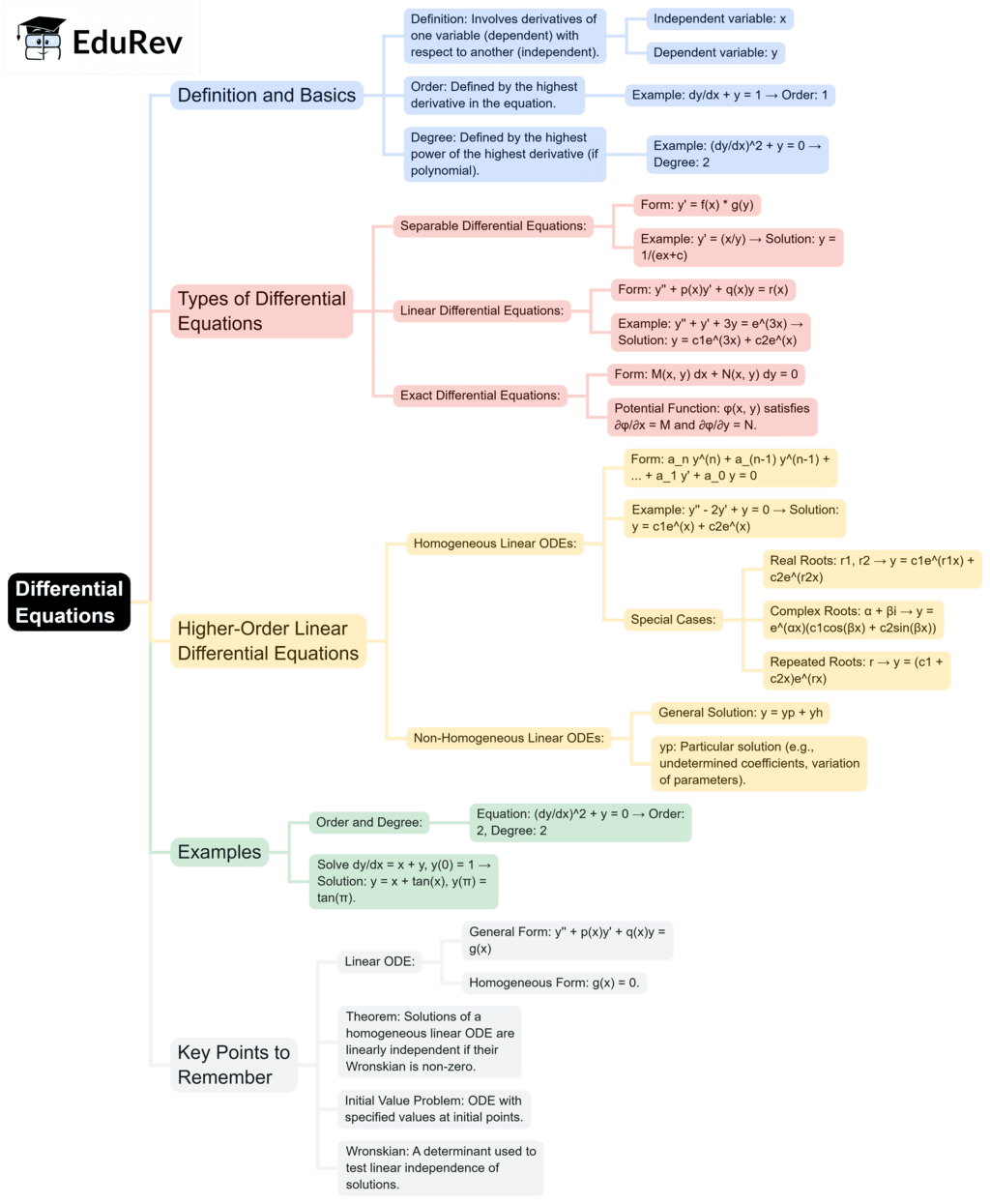
The document Mind Map: Differential Equations | Engineering Mathematics - Engineering Mathematics is a part of the Engineering Mathematics Course Engineering Mathematics.
All you need of Engineering Mathematics at this link: Engineering Mathematics
|
65 videos|129 docs|94 tests
|
FAQs on Mind Map: Differential Equations - Engineering Mathematics - Engineering Mathematics
| $1. What are differential equations and why are they important in mathematics? |  |
Ans. Differential equations are mathematical equations that relate a function to its derivatives. They are crucial because they describe how a quantity changes over time or space, making them essential for modeling real-world phenomena in physics, engineering, biology, and economics.
| $2. What are the main types of differential equations? |  |
Ans. The main types of differential equations include ordinary differential equations (ODEs), which involve functions of one variable and their derivatives, and partial differential equations (PDEs), which involve functions of multiple variables and their partial derivatives. Each type has specific methods for solving them.
| $3. How can I solve a first-order differential equation? |  |
Ans. A first-order differential equation can often be solved using separation of variables, where you rearrange the equation to isolate the variables on opposite sides. After integration, you can find the general solution, often including a constant of integration.
| $4. What is the significance of initial conditions in solving differential equations? |  |
Ans. Initial conditions specify the value of the solution or its derivatives at a certain point. They are crucial for finding a unique solution to a differential equation, especially for initial value problems, where multiple solutions may exist without these conditions.
| $5. Are there any numerical methods for solving differential equations? |  |
Ans. Yes, there are several numerical methods for solving differential equations, including Euler's method, Runge-Kutta methods, and finite difference methods. These techniques provide approximate solutions and are especially useful when analytical solutions are difficult or impossible to obtain.
Related Searches
















