Engineering Mathematics Exam > Engineering Mathematics Notes > Engineering Mathematics > Mind Map: Calculus
Mind Map: Calculus | Engineering Mathematics - Engineering Mathematics PDF Download
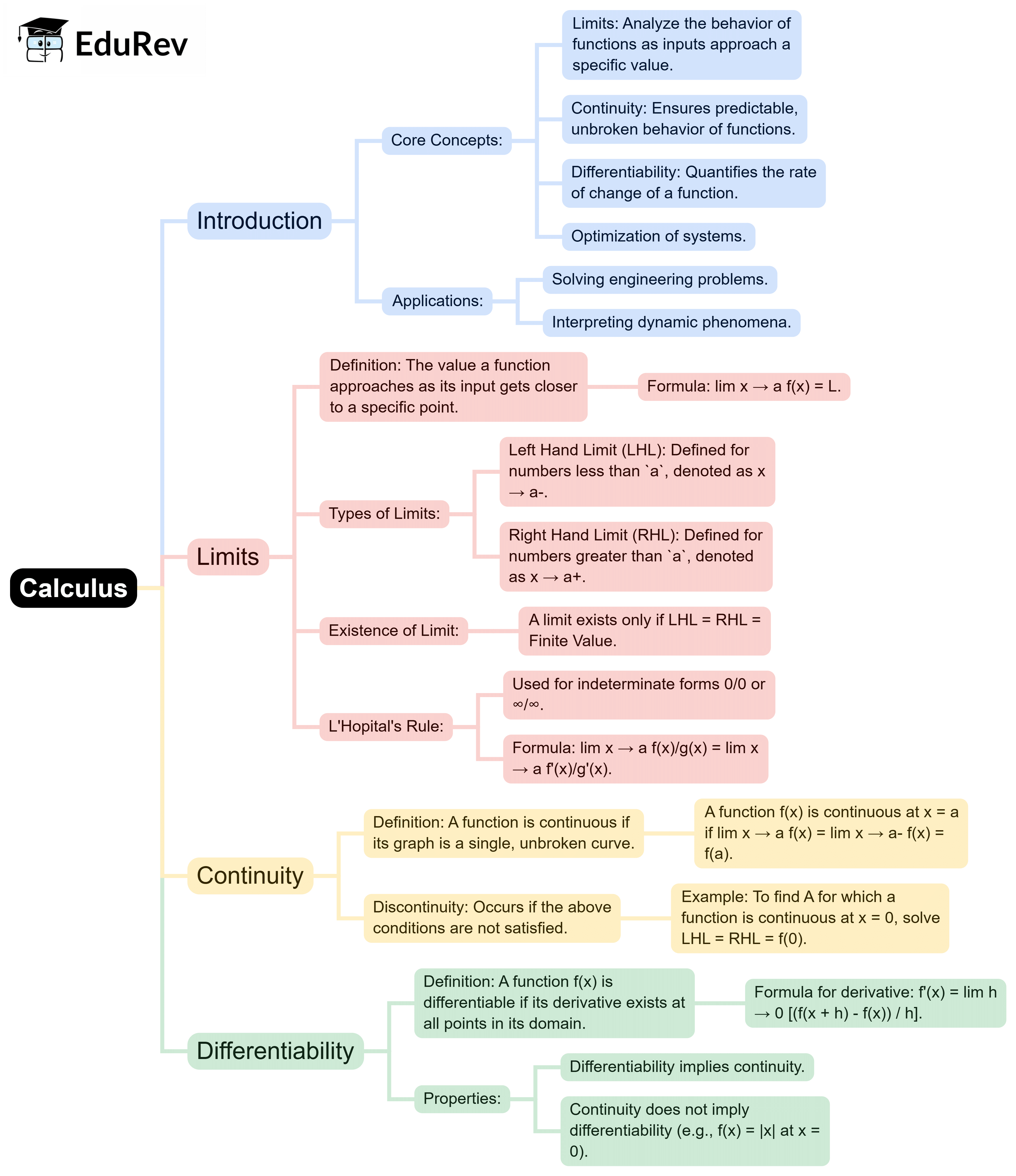
The document Mind Map: Calculus | Engineering Mathematics - Engineering Mathematics is a part of the Engineering Mathematics Course Engineering Mathematics.
All you need of Engineering Mathematics at this link: Engineering Mathematics
|
65 videos|133 docs|94 tests
|
FAQs on Mind Map: Calculus - Engineering Mathematics - Engineering Mathematics
| 1. What is the fundamental theorem of calculus and why is it important? |  |
Ans. The fundamental theorem of calculus links the concept of differentiation with integration. It states that if a function is continuous over an interval, then the integral of that function can be computed using its antiderivative. This theorem is crucial because it provides a way to evaluate definite integrals and establishes a deep connection between the two main branches of calculus.
| 2. How do you find the derivative of a function? | |
Ans. To find the derivative of a function, you can apply the limit definition of a derivative or use differentiation rules such as the power rule, product rule, quotient rule, and chain rule. The derivative represents the rate of change of the function at a particular point. For example, if you have a function f(x) = x^3, the derivative f'(x) can be found using the power rule, resulting in f'(x) = 3x^2.
| 3. What are the applications of integrals in real life? | |
Ans. Integrals have numerous applications in real life, including calculating areas under curves, determining the total accumulation of quantities (like distance traveled over time), and finding volumes of solids of revolution. They are also used in fields such as physics for calculating work done by a force, in economics for consumer and producer surplus, and in biology for population modeling.
| 4. What is the difference between definite and indefinite integrals? | |
Ans. The key difference between definite and indefinite integrals lies in their outcomes. An indefinite integral represents a family of functions and includes a constant of integration (C), while a definite integral calculates the net area under the curve between two specific points (limits) and results in a numerical value. For example, ∫ f(x) dx (indefinite) vs. ∫[a, b] f(x) dx (definite).
| 5. How do you solve limits in calculus? | |
Ans. To solve limits in calculus, you can use various techniques such as direct substitution, factoring, rationalizing, or applying L'Hôpital's rule when you encounter indeterminate forms like 0/0. The limit describes the behavior of a function as it approaches a specific point. For example, to find the limit of f(x) as x approaches 2, you would evaluate f(2) if it's defined, or apply these techniques if it leads to an indeterminate form.
About this Document
4.82/5
Rating
Sep 11, 2025
Last updated
Related Exams
Document Description: Mind Map: Calculus for Engineering Mathematics 2025 is part of Engineering Mathematics preparation.
The notes and questions for Mind Map: Calculus have been prepared according to the Engineering Mathematics exam syllabus. Information about Mind Map: Calculus covers topics
like and Mind Map: Calculus Example, for Engineering Mathematics 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Mind Map: Calculus.
Introduction of Mind Map: Calculus in English is available as part of our Engineering Mathematics
for Engineering Mathematics & Mind Map: Calculus in Hindi for Engineering Mathematics course.
Download more important topics related with notes, lectures and mock test series for Engineering Mathematics
Exam by signing up for free. Engineering Mathematics: Mind Map: Calculus | Engineering Mathematics - Engineering Mathematics
Description
Full syllabus notes, lecture & questions for Mind Map: Calculus | Engineering Mathematics - Engineering Mathematics - Engineering Mathematics | Plus excerises question with solution to help you revise complete syllabus for Engineering Mathematics | Best notes, free PDF download
Information about Mind Map: Calculus
In this doc you can find the meaning of Mind Map: Calculus defined & explained in the simplest way possible. Besides explaining types of
Mind Map: Calculus theory, EduRev gives you an ample number of questions to practice Mind Map: Calculus tests, examples and also practice Engineering Mathematics
tests
Related Searches
Mind Map: Calculus | Engineering Mathematics - Engineering Mathematics
,Extra Questions
,Exam
,practice quizzes
,Previous Year Questions with Solutions
,MCQs
,Semester Notes
,mock tests for examination
,video lectures
,Mind Map: Calculus | Engineering Mathematics - Engineering Mathematics
,Summary
,Objective type Questions
,study material
,Sample Paper
,ppt
,Important questions
,Free
,Viva Questions
,past year papers
,Mind Map: Calculus | Engineering Mathematics - Engineering Mathematics
,shortcuts and tricks
;
Additional Information about Mind Map: Calculus for Engineering Mathematics Preparation
Mind Map: Calculus Free PDF Download
The Mind Map: Calculus is an invaluable resource that delves deep into the core of the Engineering Mathematics exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Mind Map: Calculus now and kickstart your journey towards success in the Engineering Mathematics exam.
Importance of Mind Map: Calculus
The importance of Mind Map: Calculus cannot be overstated, especially for Engineering Mathematics aspirants.
This document holds the key to success in the Engineering Mathematics exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Mind Map: Calculus Notes
Mind Map: Calculus Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Mind Map: Calculus.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Mind Map: Calculus Notes on EduRev are your ultimate resource for success.
Mind Map: Calculus Engineering Mathematics Questions
The "Mind Map: Calculus Engineering Mathematics Questions" guide is a valuable resource for all aspiring students preparing for the
Engineering Mathematics exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Mind Map: Calculus on the App
Students of Engineering Mathematics can study Mind Map: Calculus alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Mind Map: Calculus,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Mind Map: Calculus is prepared as per the latest Engineering Mathematics syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup