Important Formulas: Number System | Quantitative Aptitude for Competitive Exams - SSC MTS / SSC GD PDF Download
| Table of contents |

|
| What is Number System? |

|
| Important Formulas in Number System |

|
| Important Formulas in Algebra |

|
| Types of Number System |

|
| Divisibility Rules |

|
| Other Important Topics |

|
Understanding the number system is essential for competitive exams like SSC, as it forms the basis for various quantitative sections. This topic presents interesting conceptual problems that challenge your analytical skills. Rather than simply solving problems, focus on thoroughly understanding the concepts. Explore different methods to approach questions, as it will boost your problem-solving abilities and fully prepare you for the exam.

What is Number System?
A number system, or system of numeration, is a method of representing numbers or symbols in a consistent way. In simple terms, it refers to the way numbers are written.
Here is a list of Important formulas that candidates need to master to crack the exam successfully.
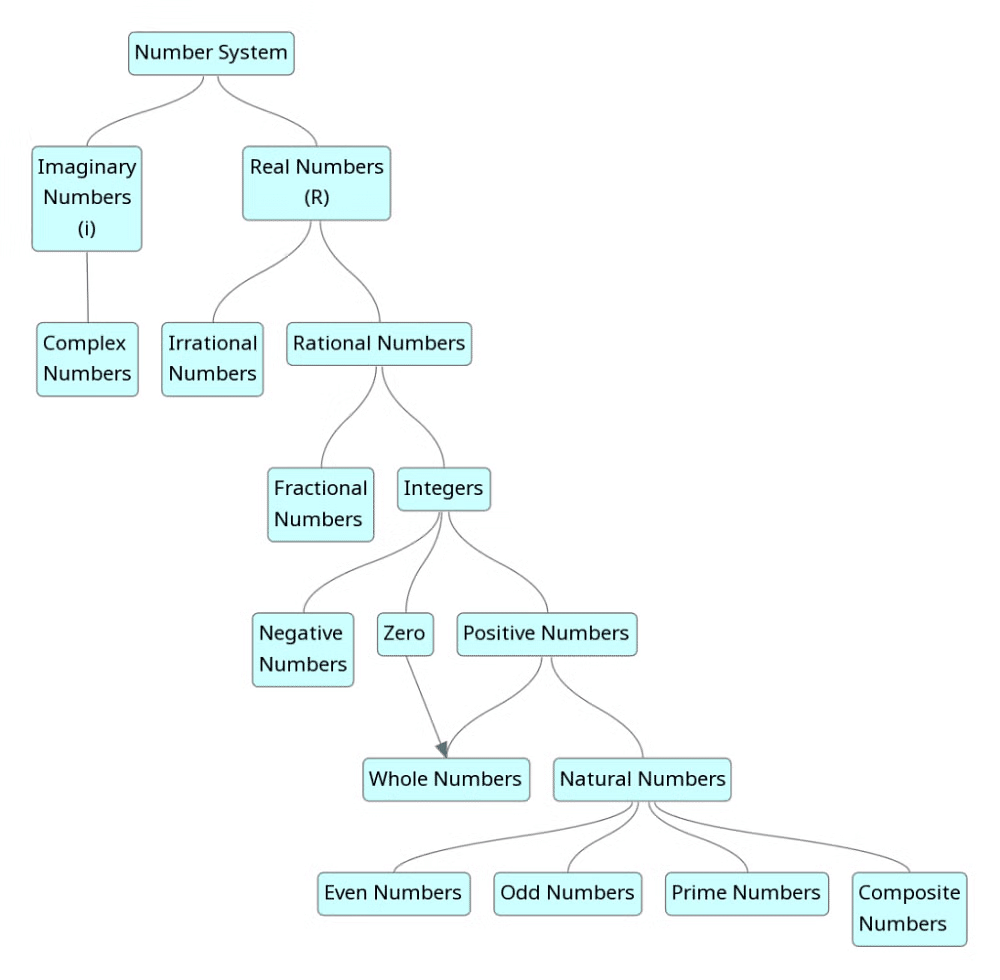
Classification of Number Systems
Number systems can be classified based on the base or the numbers used in the system. The common types include:
- Binary Number System
- Octal Number System
- Decimal Number System
- Hexadecimal Number System
These systems are widely used in computers today, while in Mathematics, we primarily use the Decimal Number System.
Decimal Number System
The term "Deci" refers to 10, so the Decimal Number System uses 10 digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. Any number can be formed using these digits, and the base of this system is also 10.
Notation of a Number
The notation of a number involves expressing it in terms of its place values. For example, the number 231 can be written as:
231 = 2 × 10² + 3 × 10¹ + 1 × 10⁰
When writing a number, the digits are read from right to left. In India, two systems are used for representing numbers:
- Indian System (or Hindu-Arabic System)
- International System
Face Value and Place Value
When representing numbers, two terms are commonly used:
- Face Value: This refers to the actual value of the digit in the number.
Example: In 38786, the face value of 7 is simply 7. - Place Value: This refers to the value of the digit considering its position in the number.
Example: In 38786, the place value of 7 is 700, which is 7 × 100.
Important Formulas in Number System
- Sum of the first n natural numbers
Formula: Example: Find the sum of the first 5 natural numbers.
Example: Find the sum of the first 5 natural numbers.
Solution: Using the formula, n = 5,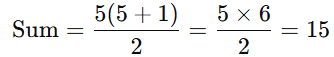
- Sum of the squares of the first n natural numbers
Formula: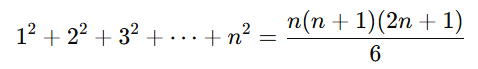 Example: Find the sum of the squares of the first 4 natural numbers.
Example: Find the sum of the squares of the first 4 natural numbers.
Solution: Using the formula, n = 4,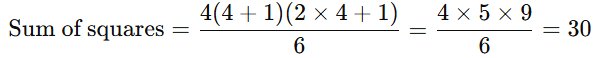
- Sum of the cubes of the first n natural numbers
Formula: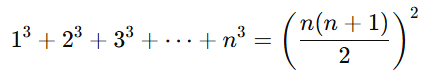 Example: Find the sum of the cubes of the first 3 natural numbers.
Example: Find the sum of the cubes of the first 3 natural numbers.
Solution: Using the formula, n = 3,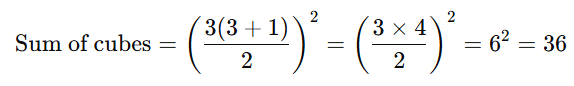
- Sum of the first n odd numbers
Formula: Sum of first n odd numbers = n2
Example: Find the sum of the first 5 odd numbers.
Solution: Using the formula, n = 5,
Sum of first 5 odd numbers = 52 = 25 - Sum of the first n even numbers
Formula: Sum of first n even numbers = n × (n + 1)
Example: Find the sum of the first 4 even numbers.
Solution: Using the formula, n = 4,
Sum of first 4 even numbers = 4 × (4 + 1) = 4 × 5 = 20
Important Formulas in Algebra
- (a + b)(a - b) = (a2 - b2)
- (a + b)2 = (a2 + b2 + 2ab)
- (a - b)2 = (a2 + b2 - 2ab)
- (a + b + c)2 = a2 + b2 + c2 + 2(ab + bc + ca)
- (a3 + b3) = (a + b)(a2 - ab + b2)
- (a3 - b3) = (a - b)(a2 + ab + b2)
- (a3 + b3 + c3 - 3abc) = (a + b + c)(a2 + b2 + c2 - ab - bc - ac)
- When a + b + c = 0, then a3 + b3 + c3 = 3abc
- (a + b)n = an + (nC1)an-1b + (nC2)an-2b² + … + (nCn-1)abn-1 + bn
Types of Number System
- Natural Numbers
All positive integers are called natural numbers. All counting numbers from 1 to infinity are natural numbers.
N = {1, 2, 3, 4, 5, 6……….∞} - Whole Numbers
The set of numbers that includes all natural numbers and the number zero are called whole numbers. They are also called as Non-negative integers.
W = { 0, 1, 2, 3, 4, 5, 6, 7, 8,…………..∞} - Integers
All numbers that do not have the decimal places in them are called integers.
Z = {∞…….-3, -2, -1, 0, 1, 2, 3………∞}
a. Positive Integers
1, 2, 3, 4….. is the set of all positive integers.
b. Negative Integers
−1, −2, −3….. is the set of all negative integers.
c. Non-Positive and Non-Negative Integers
0 is neither positive nor negative. - Real Numbers
All numbers that can be represented on the number line are called real numbers. - Rational Numbers
A rational number is defined as a number of the form a/b where ‘a’ and ‘b’ are integers and b ≠ 0. The rational numbers that are not integers will have decimal values. These values can be of two types
a. Terminating decimal fractions:
For example: 1551
= 0.5,12544125
= 31.25
b. Non-Terminating decimal fractions:
For example: 196619
= 3.1666666, 219921
= 2.33333 - Irrational Numbers
It is a number that cannot be written as a ratio form (or fraction). An Irrational numbers are non-terminating and non-periodic fractions.
For example: 22
= 1.414 - Complex Numbers
The complex numbers are the set {a+bi}, where, a and b are real numbers and ‘i’ is the imaginary unit. - Imaginary Numbers
A number does not exist on the number line is called imaginary number.
For example square root of negative numbers are imaginary numbers. It is denoted by ‘i’ or ‘j. - Even Numbers
A number divisible by 2 is called an even number.
For example: 2, 6, 8, 14, 18, 246, etc. - Odd Numbers
A number not divisible by 2 is called an odd number.
For example: 3, 7, 9, 15, 17, 373, etc. - Prime Numbers
A number greater than 1 is called a prime number, if it has exactly two factors, namely 1 and the number itself.
For example: 2, 3, 5, 7, 11, 13, 17, etc. - Composite Numbers
Numbers greater than 1 which are not prime, are known as composite numbers.
For example: 4, 6, 8, 10, etc. - Twin Prime Numbers
Twin prime numbers are pairs of prime numbers that differ by exactly 2. For example, (3, 5), (5, 7), and (11, 13) are twin primes.
Co-prime Numbers
Co-prime numbers are a pair of numbers that do not share any common factor other than 1. In other words, they have a Highest Common Factor (H.C.F) of 1. Examples include (6, 35) and (12, 25).Perfect Number
A number is considered a perfect number if the sum of its factors, excluding the number itself, equals the number. For example, 6 and 28 are perfect numbers.
The factors of 6 are 1, 2, 3, and 6, and 1 + 2 + 3 = 6.
The factors of 28 are 1, 2, 4, 7, 14, and 28, and 1 + 2 + 4 + 7 + 14 = 28.
Notes:
- 2 is the only even prime number.
- There are 15 prime numbers between 1 and 50, and their sum is 328.
- There are 25 prime numbers between 1 and 100, and their sum is 1060.
- 2 and 3 are the only consecutive prime numbers.
- 3, 5, and 7 are the only set of three twin prime numbers.
Divisibility Rules
- Divisibility by 2 → A number that is even or a number whose last digit is an even number i.e. 0, 2, 4, 6, and 8.
- Divisibility by 3 → The sum of all the digits of the number should be divisible by 3.
- Divisibility by 4 → Number formed by the last two digits of the number should be divisible by 4 or should be 00.
- Divisibility by 5 → Numbers having 0 or 5 as their ones place digit.
- Divisibility by 6 → A number that is divisible by both 2 and 3.
- Divisibility by 7 → Subtracting twice the last digit of the number from the remaining digits gives a multiple of 7.
- Divisibility by 8 → Number formed by the last three digits of the number should be divisible by 8 or should be 000.
- Divisibility by 9 → The sum of all the digits of the number should be divisible by 9.
- Divisibility by 10 → Divisibility rule for 10 states that any number whose last digit is 0, is divisible by 10.
- Divisibility by 11 → The difference of the sums of the alternative digits of a number is divisible by 11.
- Divisibility by 12 → A number that is divisible by both 3 and 4.
- Divisibility by 13 → For any given number, to check if it is divisible by 13, we have to add four times of the last digit of the number to the remaining number and repeat the process until you get a two-digit number. Now check if that two-digit number is divisible by 13 or not. If it is divisible, then the given number is divisible by 13.
- Divisibility by 14→ A number divisible by both 2 and 7.
- Divisibility by 16 → Last four-digit divisible by 16
- Divisibility by 27 → Sum of blocks of 3 (taken a right to left) divisible by 27
Solved Examples of Divisibility
Example 1: Is 7248 is divisible (i) by 4, (ii) by 2, and (iii) by 8?
(i) The number 7248 has 48 on its extreme right side which is exactly divisible by 4. When we divide 48 by 4 we get 12.
Therefore, 7248 is divisible by 4.
(ii) The number 7248 has 8 on its unit place which is an even number so, 7248 is divisible by 2.
(iii) 7248 is divisible by 8 as 7248 has 248 at its hundred place, tens place and unit place which is exactly divisible by 8.
Example 2: A number is divisible by 4 and 12. Is it necessary that it will be divisible by 48? Give another example in support of your answer.
48 = 4 × 12 but 4 and 12 are not co-prime.
Therefore, it is not necessary that the number will be divisible by 48.
Let us consider the number 72 for an example
72 ÷ 4 = 18, so 72 is divisible by 4.
72 ÷ 12 = 6, so 72 is divisible by 12.
But 72 is not divisible by 48.
Example 3: Without actual division, find if 235932 is divisible (i) by 4 and (ii) 8.
(i) The number formed by the last two digits on the extreme right side of 235932 is 32
32 ÷ 4 = 8, i.e. 32 is divisible by 4.
Therefore, 235932 is divisible by 4.
(ii) The number formed by the last three digits on the extreme right side of 235932 is 932
But 932 is not divisible by 8.
Therefore, 235932 is not divisible by 8.
Example 4: Check whether 998 is divisible by 9.
According to the rule, if the sum of the digits in a number is a multiple of 9, then it is divisible by 9.
Sum of the digits in 998: 9 + 9 + 8 = 26
26 is not a multiple of 9
So, 998 is not divisible by 9.
Example 5: Check whether 1782 is divisible by 11.
According to the rule, in a number, if the sum of the digits in odd places and sum of the digits in even places are equal or they differ by a number divisible by 11, then the number is divisible by 11.
In 1782, the sum of the digits in odd places:
1 + 8 = 9
In 1782, the sum of the digits in even places:
7 + 2 = 9
In 1782, the sum of the digits in odd places and sum of the digits in even places are equal.
So, 1782 is divisible by 11.
 |
Download the notes
Important Formulas: Number System
|
Download as PDF |
Other Important Topics
Counting Zero
In exams, questions often ask to find the number of zeros at the end of a number formed by the product of multiple numbers.
The number of zeros at the end of a number depends on the number of times 10 can be formed in the product. Since 10 is the product of 2 and 5, the number of zeros is determined by the smaller count of 2's and 5's in the factors of the product.
2n × 5n = 10n
To find the number of zeros, you need to count the factors of 2 and 5 in the expression. The number of zeros will be equal to the smaller of the two powers.
Factorial
A factorial is the product of all natural numbers from 1 to a given number N.
In simple terms, the factorial of a number is the product of all natural numbers equal to or less than that number.
N! = 1 × 2 × 3 × ⋯ × (N − 1) × N
To find the number of zeros in N!, you count the multiples of 5 in the sequence from 1 to N. This is done by dividing N by 5, then dividing the quotient by 5 again, and repeating the process until the quotient is less than 5. You add up all the quotients, disregarding the remainders.
Unit Digit
In exams, questions sometimes ask for the unit digit of an expression. It is quite simple to find the unit digit when the numbers in the expression are not in the form of powers. The unit digit can be determined by focusing on the last digits of the numbers involved in the expression.
Relation Between Dividend, Divisor, Quotient, and Remainder
The relationship between the dividend, divisor, quotient, and remainder can be expressed as:
Dividend = Divisor × Quotient + Remainder
The remainder is always a positive value, but sometimes it is useful to consider the remainder as a negative value for faster problem-solving.
To calculate a negative remainder:
Negative Remainder = Remainder − Divisor
Successive Division
In successive division, the quotient obtained from a division is used as the next dividend, and the same process continues. For example, if you divide 150 by 5, the quotient will be 30, and the remainder will be 0. Next, dividing 30 by 2 gives a quotient of 15 and a remainder of 0. Dividing 15 by 3 gives a quotient of 5 and a remainder of 0. Finally, dividing 5 by 4 gives a quotient of 1 and a remainder of 1. The process continues until the quotient is less than the divisor.
|
204 videos|108 docs|111 tests
|
FAQs on Important Formulas: Number System - Quantitative Aptitude for Competitive Exams - SSC MTS / SSC GD
| 1. What is the Number System and why is it important in mathematics? |  |
| 2. What are the important formulas related to the Number System? |  |
| 3. What are the different types of Number Systems? |  |
| 4. What are the basic divisibility rules in the Number System? |  |
| 5. What are some important formulas in Algebra related to the Number System? |  |


























