Proof of Theorems: Triangles | Mathematics (Maths) Class 10 PDF Download
| Table of contents |

|
| Theorem 1: Basic Proportionality Theorem (Thales' Theorem) |

|
| Theorem 2: Converse of Basic Proportionality Theorem |

|
| Theorem 3: SSS Similarity Criterion |

|
| Theorem 4: Pythagoras Theorem |

|
Theorem 1: Basic Proportionality Theorem (Thales' Theorem)
Statement: If a line is drawn parallel to one side of a triangle to intersect the other two sides, then it divides those sides in the same ratio.
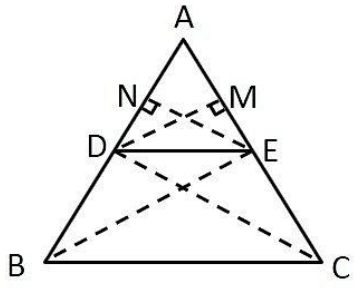 Given: In △ABC, DE is drawn parallel to BC such that it intersects AB at D and AC at E, i.e., DE || BC.
Given: In △ABC, DE is drawn parallel to BC such that it intersects AB at D and AC at E, i.e., DE || BC.
To Prove:
ADDB = AEEC
Construction: Join C to D and B to E. Draw EM ⊥ AB and DN ⊥ AC.
Proof:
Area of △ADE = 12 × AD × EM
Area of △BDE = 12 × DB × EM
Area of △ADE = 12 × AE × DN
Area of △DEC = 12 × EC × DN
Therefore, Ar(ADE)Ar(BDE) = ADDB
Similarly, Ar(ADE)Ar(DEC) = AEEC
Triangles DEC and BDE are on the same base (DE) and between the same parallels (DE || BC).
Hence, Ar(BDE) = Ar(DEC).
From the above equations, we conclude:
ADDB = AEEC
Conclusion: The theorem is proved.
Theorem 2: Converse of Basic Proportionality Theorem
Statement: If a line divides any two sides of a triangle in the same ratio, then that line is parallel to the third side.
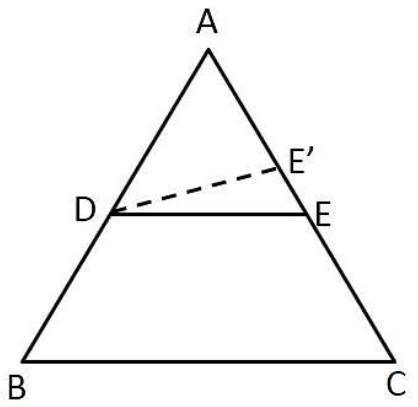 Given: In △ABC, a line DE divides AB and AC such that:
Given: In △ABC, a line DE divides AB and AC such that:
ADDB = AEEC
To Prove: DE || BC
Construction: Assume a new line DE' parallel to BC, intersecting AC at E'.
Proof:
By Thales' Theorem, since DE' || BC:
ADDB = AE'E'C
From the given condition:
ADDB = AEEC
Since E and E' satisfy the same ratio, they must coincide.
Thus, DE || BC.
Conclusion: The theorem is proved.
Theorem 3: SSS Similarity Criterion
Statement: In two triangles, if the sides of one triangle are proportional to the sides of another triangle, then their corresponding angles are equal, and hence the triangles are similar.
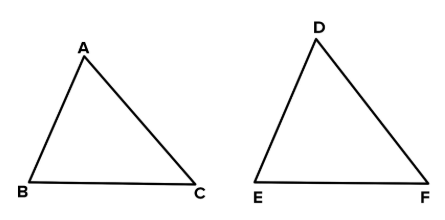 Given: Two triangles △ABC and △DEF such that:
Given: Two triangles △ABC and △DEF such that:
ABDE = ACDF = BCEF
To Prove: △ABC ~ △DEF
Proof:
Since it is given that:
ABDE = ACDF = BCEF
The corresponding sides of △ABC and △DEF are in the same ratio.
We now place △ABC and △DEF such that:
- AB corresponds to DE
- AC corresponds to DF
- BC corresponds to EF
By construction, when the sides of two triangles are proportional, their corresponding **angles must be equal**. Thus, we get:
∠A = ∠D, ∠B = ∠E, ∠C = ∠F
Since all three pairs of corresponding angles are equal, by the **AAA (Angle-Angle-Angle) Similarity Criterion**, we conclude that:
△ABC ~ △DEF
Conclusion: The theorem is proved.
Theorem 4: Pythagoras Theorem
Statement: In a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
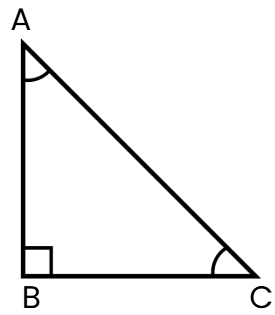 Given: In △ABC, ∠B = 90°, AC is the hypotenuse.
Given: In △ABC, ∠B = 90°, AC is the hypotenuse.
To Prove:
AC2 = AB2 + BC2
Construction: Draw BD ⊥ AC from B to AC.
Proof:
In △ABC and △ADB:
ABAC = ADAB
Multiplying both sides by AC:
AB2 = AC × AD
Similarly, in △ABC and △BDC:
BCAC = CDBC
Multiplying both sides by AC:
BC2 = AC × CD
Adding both results:
AB2 + BC2 = AC × AD + AC × CD
Since AD + CD = AC, we get:
AB2 + BC2 = AC2
Conclusion: The theorem is proved.
|
127 videos|584 docs|79 tests
|
FAQs on Proof of Theorems: Triangles - Mathematics (Maths) Class 10
| 1. What is Thales' Theorem and how does it apply to triangles? |  |
| 2. What is the Converse of the Basic Proportionality Theorem? |  |
| 3. What is the SSS Similarity Criterion in triangles? |  |
| 4. Can you explain the Pythagorean Theorem and its significance in triangle geometry? |  |
| 5. How can the theorems related to triangles help in solving real-world problems? |  |
















