Notes: ज्यामिति | गणित और शिक्षाशास्त्र (Mathematics) CTET & TET Paper 1 - CTET & State TET PDF Download
| Table of contents |

|
| मूल ज्यामितीय शर्तें |

|
| रेखाओं के प्रकार |

|
| रेखखंड की माप |

|
| रेखा खंड बनाना |

|
| कोण |

|
| टैंग्राम |

|
| क्षेत्रफल |

|
ज्यामिति गणित की एक शाखा है जो बिंदुओं, रेखाओं, सतहों और ठोस आकृतियों के गुणों और संबंधों से संबंधित है। यह कला, वास्तुकला, अभियंत्रण और विभिन्न विज्ञान की शाखाओं सहित कई क्षेत्रों के लिए मौलिक है। केंद्रीय शिक्षक पात्रता परीक्षा (CTET) के लिए, ज्यामिति की गहरी समझ आवश्यक है, विशेष रूप से प्राथमिक और उच्च प्राथमिक स्तर पर गणित पढ़ाने के लिए।
मूल ज्यामितीय शर्तें
1. बिंदु
एक बिंदु को (.) द्वारा दर्शाया जाता है।
यह एक plane या space में एक सटीक स्थान का प्रतिनिधित्व करता है।
इसका कोई लंबाई और चौड़ाई नहीं होती। हम एक बिंदु को एक बड़े अक्षर से दर्शाते हैं, जैसा कि नीचे दिखाया गया है।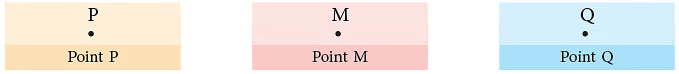
2. रेखा खंड
एक कागज पर दो बिंदुओं को चिन्हित करें और उन्हें A और B नाम दें।  एक शासक का उपयोग करके इन बिंदुओं को जोड़ें। जो आकृति प्राप्त होती है उसे रेखा खंड कहा जाता है। रेखा खंड के दो अंत बिंदु होते हैं। इसे अंत बिंदुओं के द्वारा नामित किया जाता है, जैसे रेखा खंड AB।
एक शासक का उपयोग करके इन बिंदुओं को जोड़ें। जो आकृति प्राप्त होती है उसे रेखा खंड कहा जाता है। रेखा खंड के दो अंत बिंदु होते हैं। इसे अंत बिंदुओं के द्वारा नामित किया जाता है, जैसे रेखा खंड AB।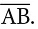

3. रेखा
एक रेखा खंड को दोनों तरफ बिना अंत के बढ़ाया जाता है, उसे रेखा कहा जाता है।
एक रेखा के अंत बिंदु नहीं होते। एक रेखा को उस पर किसी भी दो बिंदुओं को लेकर दर्शाया जाता है। उदाहरण के लिए, इस रेखा को  नामित करने के लिए, हम उस पर दो बिंदुओं को चिन्हित करते हैं, जैसे A और B। इसे (रेखा AB) कहा जाता है और इसे इस प्रकार दर्शाया जाता है।
नामित करने के लिए, हम उस पर दो बिंदुओं को चिन्हित करते हैं, जैसे A और B। इसे (रेखा AB) कहा जाता है और इसे इस प्रकार दर्शाया जाता है। 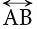
 आमतौर पर, हम एक सीधी रेखा के लिए शब्द रेखा का उपयोग करते हैं। सीधी रेखा ऊर्ध्वाधर, क्षैतिज या तिरछी हो सकती है।
आमतौर पर, हम एक सीधी रेखा के लिए शब्द रेखा का उपयोग करते हैं। सीधी रेखा ऊर्ध्वाधर, क्षैतिज या तिरछी हो सकती है।
4. रे
एक रे एक सीधा पथ है जिसमें एक अंत बिंदु होता है और यह एक दिशा में निरंतर चलता है।
यह रे A बिंदु से शुरू होती है और B बिंदु से होकर गुजरती है।
यह B पर रुकती नहीं है। हम दिए गए रे को 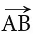 (रे AB) नामित करते हैं, जहाँ पहला अक्षर हमेशा अंत बिंदु होता है।
(रे AB) नामित करते हैं, जहाँ पहला अक्षर हमेशा अंत बिंदु होता है।  प्रतीक → दिखाता है कि एक रे का एक निश्चित अंत बिंदु होता है और यह दूसरी दिशा में अनंत तक बढ़ती है। एक टॉर्च से निकलने वाली रोशनी की रेखाएँ और सूर्य की किरणें रे के सबसे सामान्य उदाहरण हैं।
प्रतीक → दिखाता है कि एक रे का एक निश्चित अंत बिंदु होता है और यह दूसरी दिशा में अनंत तक बढ़ती है। एक टॉर्च से निकलने वाली रोशनी की रेखाएँ और सूर्य की किरणें रे के सबसे सामान्य उदाहरण हैं। 5. समतल
5. समतल
एक समतल एक सपाट सतह होती है।
गणित में, एक समतल का अर्थ है जो सभी दिशाओं में बिना किसी अंत के चलता है। हम आमतौर पर समतल के केवल एक भाग के साथ काम करते हैं। बिंदु और रेखाएँ एक समतल पर स्थित होती हैं। किसी समतल का नाम उसके ऊपर के किसी भी तीन बिंदुओं का उपयोग करके रखा जा सकता है। दी गई आकृति समतल PQR को दर्शाती है। बिंदुओं का क्रम मायने नहीं रखता।
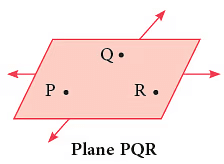
आपके दैनिक जीवन में समतल सतह के कुछ प्रतिनिधित्व इस प्रकार हैं:

रेखाओं के प्रकार
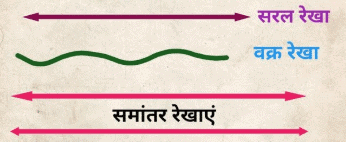
1. समानांतर रेखाएँ
एक ही समतल पर जो रेखाएँ कभी नहीं मिलतीं, चाहे उन्हें कितना भी बढ़ाया जाए, उन्हें समानांतर रेखाएँ कहा जाता है।
वे हमेशा समान दूरी पर होती हैं। '||' प्रतीक का उपयोग ‘‘समानांतर है’’ दिखाने के लिए किया जाता है।
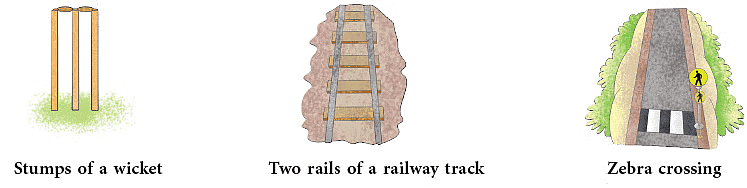
यहाँ, रेखा XY रेखा PQ के समानांतर है और रेखा LM || रेखा AB है। 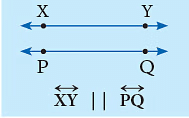 दैनिक जीवन में समानांतर रेखाओं के कुछ प्रतिनिधित्व इस प्रकार हैं:
दैनिक जीवन में समानांतर रेखाओं के कुछ प्रतिनिधित्व इस प्रकार हैं:
2. अवयव रेखाएँ
जो रेखाएँ एक बिंदु पर मिलती हैं, उन्हें अवयव रेखाएँ कहा जाता है।
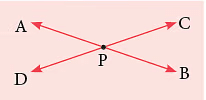 दिए गए चित्र में,
दिए गए चित्र में,
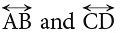
ये बिंदु P पर मिलती हैं। अवयव रेखाओं या रेखा खंडों के कुछ उदाहरण इस प्रकार हैं:

3. लंबवत रेखाएँ
जब दो अवयव रेखाएँ मिलकर समकोण बनाती हैं, तो उन्हें लंबवत रेखाएँ कहा जाता है।
इनका संकेत
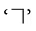 (एक वर्गीय कोने) में किया जाता है। रेखा AB रेखा CD के लंबवत है और इसे संक्षेप में लिखा जाता है।
(एक वर्गीय कोने) में किया जाता है। रेखा AB रेखा CD के लंबवत है और इसे संक्षेप में लिखा जाता है।
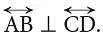
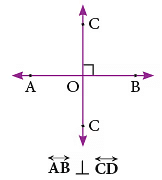 'L' एक लंबवत रेखा खंड का उदाहरण है। '⊥' प्रतीक का उपयोग ‘‘लंबवत है’’ के लिए किया जाता है।
'L' एक लंबवत रेखा खंड का उदाहरण है। '⊥' प्रतीक का उपयोग ‘‘लंबवत है’’ के लिए किया जाता है।

रेखखंड की माप
रेखखंड की लंबाई मापने के लिए स्केल का उपयोग करना
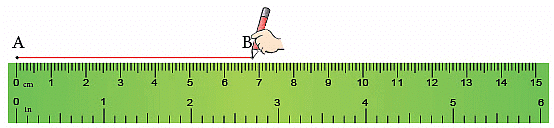
आइए हम नीचे दिए गए रेखखंड AB को मापते हैं। हम निम्नलिखित चरणों का पालन करते हैं।
- चरण 1: स्केल को रेखखंड AB के साथ रखें। स्केल का जीरो (0) निशान रेखखंड के एक छोर, बिंदु A के साथ मेल खाना चाहिए।

- चरण 2: रेखखंड के दूसरे छोर, अर्थात् बिंदु B पर स्केल पर निशान को पढ़ें। यहाँ, बिंदु B स्केल के 5.5 सेंटीमीटर निशान पर है। इसलिए, रेखखंड AB की लंबाई 5.5 सेंटीमीटर है।
रेखा खंड बनाना
एक दिए गए लंबाई, जैसे 6.8 सेमी, का रेखा खंड बनाने के लिए, हम निम्नलिखित चरणों का पालन करते हैं।
- चरण 1: एक कागज़ की शीट लें और उस पर एक बिंदु, मान लीजिए A, को तेज पेंसिल से चिह्नित करें।

- चरण 2: रूलर को बिंदु A पर उसकी शून्य (0) मार्क के साथ रखें, जैसा कि दिखाया गया है।
- चरण 3: पेंसिल को बिंदु A पर रखें और 6 के बाद 8 छोटे विभाजनों के लिए पेंसिल को बढ़ाएं। इससे AB नामक 6.8 सेमी लंबाई का रेखा खंड प्राप्त होता है।
कोण
एक कोण वह आकृति है जो दो किरणों द्वारा एक सामान्य अंत बिंदु पर मिलकर बनती है।
सामान्य अंत बिंदु को कोण का शिखर कहा जाता है और इन दो किरणों को कोण की भुजाएँ कहा जाता है। इन चित्रों को देखकर, आप एक कोण की कुछ धारणा बना सकते हैं:
कोण का प्रतीक ∠ है।
1. कोण का नामकरण
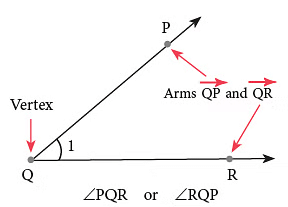
आप एक कोण को तीन तरीकों से नामित कर सकते हैं:
- तीन-अक्षर वाले नाम का उपयोग करके: एक किरण पर एक बिंदु, शिखर और दूसरी किरण पर एक बिंदु। ∠PQR या ∠RQP
- केवल एक-अक्षर वाले नाम का उपयोग करके, यानी शिखर ∠Q। (यह तब उपयोग किया जा सकता है जब इस शिखर के साथ केवल एक कोण हो।)
- कोण को नामित करने के लिए एक संख्या का उपयोग करना, यानी ∠1।
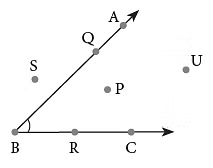
2. कोण का आंतरिक और बाह्य क्षेत्र
किरणों के बीच का क्षेत्र, यानी एक कोण के अंदर, को कोण का आंतरिक क्षेत्र कहा जाता है और कोण की भुजाओं के बाहर का क्षेत्र को कोण का बाह्य क्षेत्र कहा जाता है।
बिंदु P कोण के आंतरिक क्षेत्र में है, जबकि बिंदु S और U कोण के बाह्य क्षेत्र में हैं। बिंदु Q और R कोण की भुजाओं पर स्थित हैं।
कोणों का माप
कोण के माप से हमारा तात्पर्य घुमाव या मोड़ की मात्रा से है।
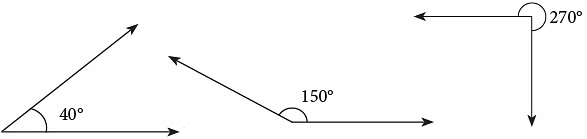
जैसे लंबाई, क्षेत्र, वजन आदि के लिए मानक इकाइयाँ होती हैं, वैसे ही कोणों के माप के लिए भी मानक इकाइयाँ होती हैं। कोणों के माप की मानक इकाई डिग्री है। डिग्री का प्रतीक ° है। एक पूर्ण घुमाव द्वारा निर्मित कोण का माप 360 डिग्री या 360° होता है। नीचे दिए गए उदाहरण को देखें। नीचे की चित्रण में 40°, 150° और 270° के कोण दिखाए गए हैं।
Edurev Tips: एक पूर्ण घुमाव को 360 समान भागों में विभाजित किया गया है।
एक भाग का माप एक डिग्री या 1° कहलाता है।
नीचे दिए गए घड़ियों को देखें: 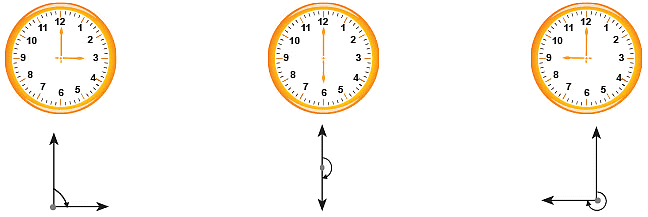 एक घड़ी की सुई एक स्थिति से दूसरी स्थिति में जाती है जब यह अपनी दिशा बदलती है। इस दिशा में परिवर्तन या मोड़ को एक बिंदु से दो तीर खींचकर दर्शाया जा सकता है।
एक घड़ी की सुई एक स्थिति से दूसरी स्थिति में जाती है जब यह अपनी दिशा बदलती है। इस दिशा में परिवर्तन या मोड़ को एक बिंदु से दो तीर खींचकर दर्शाया जा सकता है।
 साथ की चित्रण में एक पूर्ण घुमाव दिखाया गया है।
साथ की चित्रण में एक पूर्ण घुमाव दिखाया गया है।
हाथ को उसकी प्रारंभिक स्थिति में वापस लाने के लिए सबसे कम मात्रा का मोड़ एक पूर्ण घुमाव कहलाता है।
उदाहरण 1: यदि एक वृत्त को 20 समान भागों में विभाजित किया जाए, तो प्रत्येक भाग के कोण का माप क्या होगा?
एक पूर्ण घुमाव द्वारा निर्मित कोण = 360°।
∴ 20 समान भागों में से प्रत्येक का कोण = 360° / 20 = 18°।
उदाहरण 2: प्रत्येक पहिए पर पड़ोसी तीलियों के बीच के कोण की गणना करें।
(क) 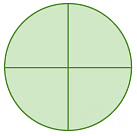 (ख)
(ख)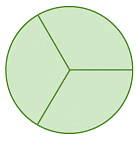 (ग)
(ग)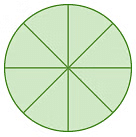
(क) चूंकि पहिया (वृत्त) को 4 समान भागों में विभाजित किया गया है, पड़ोसी तीलियों के बीच का कोण = 360° / 4 = 90°।
(ख) पहिया को 3 समान भागों में विभाजित किया गया है, इसलिए पड़ोसी तीलियों के बीच का कोण = 360° / 3 = 120°।
(ग) पहिया को 8 समान भागों में विभाजित किया गया है, इसलिए पड़ोसी तीलियों के बीच का कोण = 360° / 8 = 45°।
कोण मापना
कोण मापने के लिए उपयोग किया जाने वाला यंत्र को प्रोट्रेक्टर कहा जाता है।
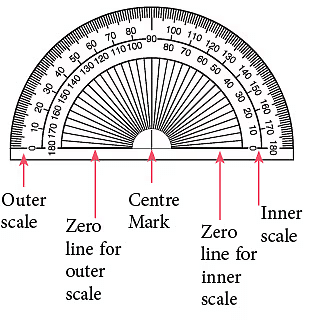
दाएँ चित्र में एक प्रोट्रेक्टर दिखाया गया है। इसका आकार अर्ध-गोल होता है और केंद्र पर कोण को 180° में विभाजित किया गया है।
Edurev Tips: प्रोट्रेक्टर का आंतरिक स्केल 0° से 180° तक वामावर्त मार्क किया गया है। प्रोट्रेक्टर का बाहरी स्केल 0° से 180° तक दक्षिणावर्त मार्क किया गया है। प्रत्येक छोटे विभाजन का मान 1° होता है।
1. 180° से कम कोण मापने के लिए
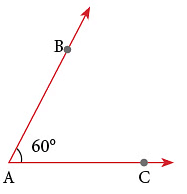
चरण 1: प्रोट्रेक्टर के केंद्र को कोण के शीर्ष पर रखें।
चरण 2: सुनिश्चित करें कि प्रोट्रेक्टर की 0° रेखा कोण के एक भुजा (AC) के साथ हो।
चरण 3: प्रोट्रेक्टर पर मान को पढ़ें जैसा कि कोण की दूसरी भुजा (AB) द्वारा संकेतित है। इस प्रकार, ∠ BAC = 60°।
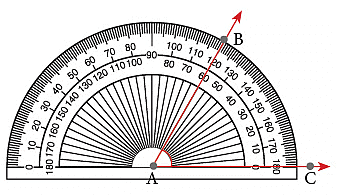
2. 180° से अधिक कोण मापने के लिए
मान लीजिए, आपको ∠x मापना है।
चरण 1: ∠a मापें।
चरण 2: फिर, रिफ्लेक्स ∠BOC = 360° – a°।
चरण 2: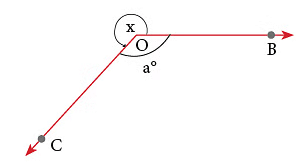
प्रोट्रैक्टर का उपयोग करके कोण खींचना
80° का कोण खींचने के लिए।
चरण 1: कोई भी किरण OA खींचें। 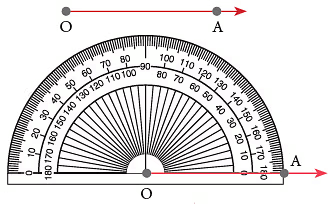 चरण 2: प्रोट्रैक्टर को इस तरह रखें कि इसका केंद्र चिह्न O, किरण के अंतिम बिंदु पर पड़ जाए। किरण को प्रोट्रैक्टर के 0° चिह्न के साथ संरेखित करें। किरण के अंतिम बिंदु O को कोण का शीर्षांक माना जाएगा।
चरण 2: प्रोट्रैक्टर को इस तरह रखें कि इसका केंद्र चिह्न O, किरण के अंतिम बिंदु पर पड़ जाए। किरण को प्रोट्रैक्टर के 0° चिह्न के साथ संरेखित करें। किरण के अंतिम बिंदु O को कोण का शीर्षांक माना जाएगा।
चरण 3: जिस स्केल पर किरण OA 0° के साथ संरेखित है, उस पर 80° पर बिंदु चिह्नित करें। बिंदु को B के रूप में लेबल करें। 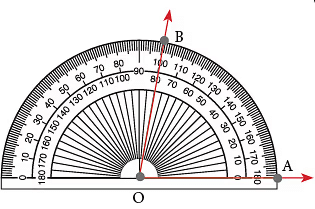 चरण 4: प्रोट्रैक्टर को हटा दें और B को O से जोड़ें।
चरण 4: प्रोट्रैक्टर को हटा दें और B को O से जोड़ें।
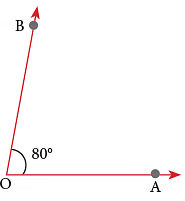
इस प्रकार, ∠AOB आवश्यक कोण है।
जैसा कि आप देख सकते हैं, हमने प्रोट्रैक्टर के अंदरूनी स्केल का उपयोग करके यह कोण खींचा है। यदि हम प्रोट्रैक्टर के बाहरी स्केल का उपयोग करें, तो कोण कैसा होगा?
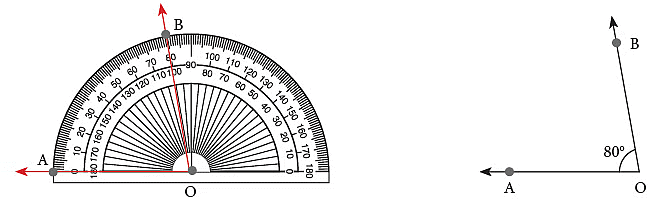
निम्नलिखित कोणों का अवलोकन करें।
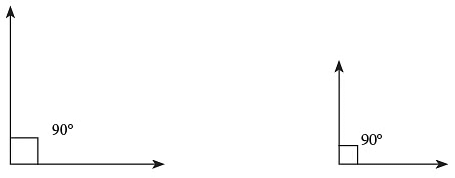
भुजाओं की लंबाई की परवाह किए बिना, प्रत्येक कोण = 90° है।
कोणों के प्रकार
कोण को 90° और 180° तथा 180° और 360° के बीच के माप के अनुसार नामित किया जाता है। निम्नलिखित चित्रों पर ध्यान दें। सीता एक रोलर कोस्टर पर बैठी है। उसकी स्थिति A है। रोलर कोस्टर विपरीत घड़ी की दिशा में चलना शुरू करता है और इस गति से सीता की स्थिति में परिवर्तन आता है।
कोणों के प्रमुख प्रकार निम्नलिखित हैं:
1. समकोण (Right Angle)
- जिसका मान 90° होता है।
- उदाहरण: वर्ग और आयत के कोने।
2. न्यूनकोण (Acute Angle)
- जिसका मान 90° से कम होता है।
- उदाहरण: त्रिकोण में छोटे कोण।
3. अधिककोण (Obtuse Angle)
- जिसका मान 90° से अधिक लेकिन 180° से कम होता है।
- उदाहरण: झुके हुए दरवाजे का कोण।
4. समलंब कोण (Straight Angle)
- जिसका मान ठीक 180° होता है।
- उदाहरण: एक सीधी रेखा।
5. पूर्ण कोण (Complete Angle)
- जिसका मान 360° होता है।
- उदाहरण: घड़ी की सुई का पूरा एक चक्कर।
6. प्रतिबिंब कोण (Reflex Angle)
- जिसका मान 180° से अधिक लेकिन 360° से कम होता है।
- उदाहरण: दरवाजे का आधे से अधिक खुला झुकाव।
समान कोण या समकोण
जब दो कोणों का माप समान होता है, तो हम कहते हैं कि वे समान या समकोण हैं और इसे ∠ABC = ∠DEF के रूप में लिखते हैं।
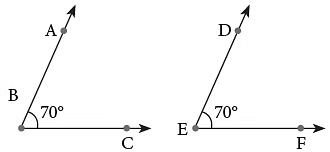 इसका अर्थ है कि एक कोण दूसरे कोण पर सटीक रूप से बैठ सकता है।
इसका अर्थ है कि एक कोण दूसरे कोण पर सटीक रूप से बैठ सकता है।
खुले और बंद आकार
1. खुले आकार
वे आकार जो एक ही बिंदु पर शुरू और समाप्त नहीं होते हैं, उन्हें खुले आकार कहा जाता है।
निम्नलिखित खुले आकारों पर ध्यान दें:

2. बंद आकार
वे आकार जो एक ही बिंदु पर शुरू और समाप्त होते हैं, उन्हें बंद आकार कहा जाता है।
निम्नलिखित बंद आकारों पर ध्यान दें:
(i) सरल बंद आकृतियाँ
निम्नलिखित आकृतियों पर ध्यान दें: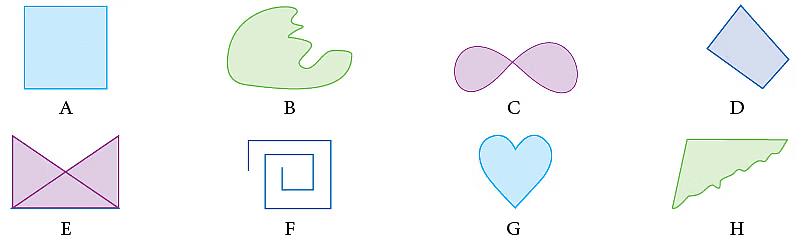 ऊपर दिए गए आकृतियों में से आप कौन-सी आकृति को किसी बिंदु से शुरू करके, बिना अपने पेंसिल को कागज से उठाए, शुरू करने के बिंदु पर समाप्त कर सकते हैं? स्पष्ट रूप से, A, B, C, D, G और H।
ऊपर दिए गए आकृतियों में से आप कौन-सी आकृति को किसी बिंदु से शुरू करके, बिना अपने पेंसिल को कागज से उठाए, शुरू करने के बिंदु पर समाप्त कर सकते हैं? स्पष्ट रूप से, A, B, C, D, G और H।
ऐसी आकृतियों को बंद आकृतियाँ कहा जाता है। इनमें से, कौन-सी आकृतियाँ आप बिना आकृति को स्वयं पार किए खींच सकते हैं?
उत्तर: A, B, D, G और H। ऐसी आकृतियों को सरल बंद आकृतियाँ कहा जाता है।
टैंग्राम
टैंग्राम एक चीनी पहेली है जो ज्यामितीय आकृतियों का उपयोग करके बनाई जाती है। आप रंगीन शीट्स को पाँच त्रिकोण, एक वर्ग, और एक समांतर चतुर्भुज में काटकर टैंग्राम बना सकते हैं। इन सात ज्यामितीय आकृतियों को, जिन्हें टैंस कहा जाता है, विभिन्न तरीकों से संयोजित किया जा सकता है ताकि विभिन्न रूप बनाए जा सकें। जब आप इन टुकड़ों को एक साथ व्यवस्थित करते हैं, तो वे विभिन्न आकृतियों का प्रतिनिधित्व कर सकते हैं और कई गणितीय और ज्यामितीय विचारों को स्पष्ट कर सकते हैं। टैंग्राम के टुकड़ों का सामान्यतः पहेलियों को हल करने के लिए उपयोग किया जाता है। दिलचस्प बात यह है कि सभी सात टुकड़ों को मिलाकर एक वर्ग बनाया जा सकता है। नीचे दी गई आकृति एक सात-टुकड़े वाले टैंग्राम को दर्शाती है।

हम टांग्राम का उपयोग क्यों करते हैं?
हम टांग्राम का उपयोग करते हैं क्योंकि ये विशेष निर्माण ब्लॉक्स की तरह होते हैं जो हमें समस्याओं को हल करने और स्मार्ट तरीके से सोचने में मदद करते हैं। टांग्राम हमें आकृतियों को समझने, चीजों के एक साथ फिट होने का पता लगाने और रचनात्मक होने में भी मदद करते हैं। ये हमें महत्वपूर्ण गणितीय विचार सिखाते हैं जैसे कि आकृतियों का मिलान करना, चीजों को समानांतर बनाना, आकृतियों के अंदर का स्थान खोजना, और आकृतियों के चारों ओर के आकार को समझना। जो बच्चे टांग्राम का उपयोग करते हैं, वे गणित परीक्षणों में भी बेहतर कर सकते हैं, और टांग्राम से बनाने के लिए बहुत सारी मजेदार आकृतियाँ और चित्र हैं, जो 6,500 से अधिक हैं।

क्षेत्रफल
क्षेत्रफल यह दर्शाता है कि एक समतल आकृति कितनी जगह घेरती है। यह ऐसा है जैसे आकृति के अंदर समाने वाले छोटे वर्गों की संख्या को गिनना। हम क्षेत्रफल को वर्ग इकाइयों में मापते हैं, जैसे कि वर्ग इंच या वर्ग फुट। यदि आप किसी आकृति का क्षेत्रफल ज्ञात करना चाहते हैं, तो आपको यह पता करना होगा कि वह कितने छोटे वर्गों को समा सकती है। विभिन्न आकृतियों, जैसे कि वर्ग, आयत, आदि के लिए क्षेत्रफल निकालने के विभिन्न तरीके हैं।
वर्ग और आयत
वर्ग और आयत के लिए, आप क्षेत्रफल को लंबाई और चौड़ाई को गुणा करके निकाल सकते हैं।
क्षेत्रफल = लंबाई × चौड़ाई
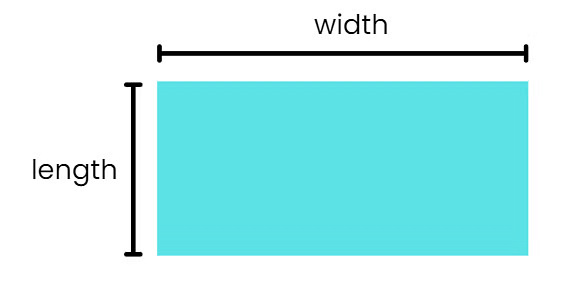
उदाहरण: यदि आपके पास एक आयत है जिसकी लंबाई 5 इकाई है और चौड़ाई 3 इकाई है,
क्षेत्रफल = 5 इकाई × 3 इकाई = 15 वर्ग इकाई
त्रिकोण
त्रिकोणों के लिए, आप क्षेत्रफल को आधार और ऊँचाई को गुणा करके और फिर 2 से भाग देकर खोज सकते हैं।
क्षेत्रफल = (आधार × ऊँचाई) ÷ 2
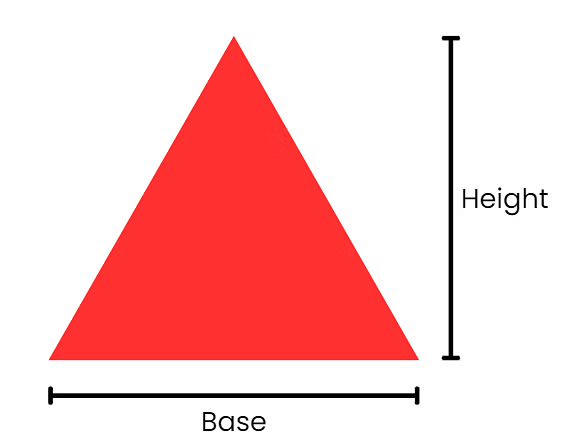
उदाहरण: यदि आपके पास 4 इकाइयों का आधार और 6 इकाइयों की ऊँचाई वाला एक त्रिकोण है,
क्षेत्रफल = (4 इकाइयाँ × 6 इकाइयाँ) ÷ 2 = 12 वर्ग इकाइयाँ
वृत्त
वृत्तों के लिए, आप क्षेत्रफल को सूत्र A = πr² (जहाँ π पाइ है और r त्रिज्या है) का उपयोग करके खोज सकते हैं।
क्षेत्रफल = π × (त्रिज्या × त्रिज्या)
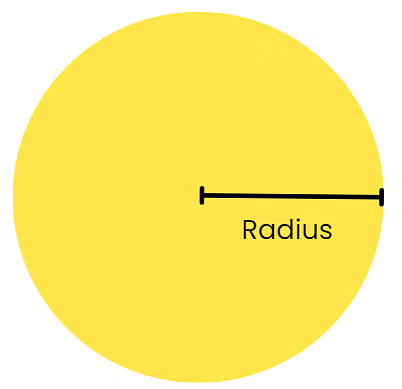
उदाहरण: यदि आपके पास 2 इकाइयों की त्रिज्या वाला एक वृत्त है,
क्षेत्रफल = π × (2 इकाइयाँ × 2 इकाइयाँ) ≈ 12.57 वर्ग इकाइयाँ
निम्नलिखित वस्तुओं को देखें।
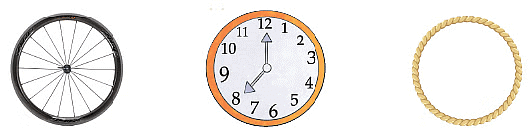 उपर्युक्त वस्तुओं में से सभी आकार आपको किस आकृति की याद दिलाते हैं? ये सभी वस्तुएँ वृत्त के आकार की हैं।
उपर्युक्त वस्तुओं में से सभी आकार आपको किस आकृति की याद दिलाते हैं? ये सभी वस्तुएँ वृत्त के आकार की हैं।
वृत्त एक साधारण बंद वक्र है।
Edurev Tips: एक वृत्त बहुभुज नहीं है क्योंकि यह सीधे रेखाओं से नहीं बना है।
वृत्त खींचना
हम इन विधियों में से किसी एक का उपयोग करके वृत्त खींच सकते हैं।
विधि:
- किसी भी गोल वस्तु जैसे सिक्का, बोतल का ढक्कन, चूड़ी आदि लें और उसकी आकृति को ट्रेस करें। आपको वृत्त का आकार मिलेगा।
- एक धागे का टुकड़ा लें और उसके एक सिरे पर एक पेंसिल बांधें। धागे के दूसरे सिरे को कागज पर एक पिन से ठीक करें। धागे को मजबूती से पकड़ें और पेंसिल को घुमाएँ। जो आकार आपको मिलेगा वह वृत्त होगा।
- कम्पास का उपयोग करें, जिसमें एक सिरे पर धातु की नोक और दूसरे सिरे पर पेंसिल धारक होता है।
कम्पास का उपयोग करके वृत्त खींचने के लिए:
चरण 1: कम्पास पर पेंसिल को मजबूती से बांधें। पेंसिल को इस तरह समायोजित करें कि नोक और पेंसिल के किनारे एक ही स्तर पर हों। 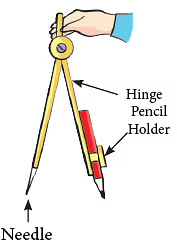 चरण 2: कम्पास की नोक को कागज की शीट पर ठीक करें।
चरण 2: कम्पास की नोक को कागज की शीट पर ठीक करें। 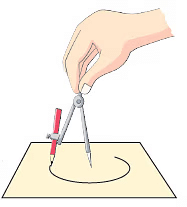 चरण 3: कम्पास की दूसरी भुजा को खींचें, जो पेंसिल को पकड़ती है।
चरण 3: कम्पास की दूसरी भुजा को खींचें, जो पेंसिल को पकड़ती है।
चरण 4: पेंसिल को चारों ओर घुमाएँ ताकि वृत्त खींचा जा सके।
वृत्त के भाग
- केन्द्र: दिए गए चित्र में, O वह बिंदु है जहाँ हम वृत्त बनाने के लिए कंपास का धातु अंत रखते हैं। O को वृत्त काकेन्द्र कहा जाता है।
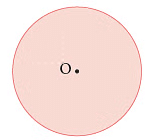 हम वृत्त का नाम उसके केन्द्र के साथ रखते हैं।
हम वृत्त का नाम उसके केन्द्र के साथ रखते हैं। - त्रिज्या: वृत्त के केन्द्र से वृत्त पर किसी भी बिंदु तक जाने वाली रेखा खंड कोत्रिज्या कहा जाता है।
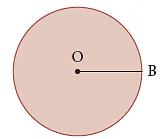 चित्र में, रेखा खंड OB वृत्त की त्रिज्या है।
चित्र में, रेखा खंड OB वृत्त की त्रिज्या है। - कोर्ड: किसी वृत्त पर किसी भी दो बिंदुओं को जोड़ने वाले रेखा खंड कोकोर्ड कहा जाता है।
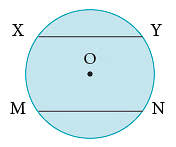 चित्र में, XY और MN वृत्त के कोर्ड हैं।
चित्र में, XY और MN वृत्त के कोर्ड हैं। - व्यास: वह कोर्ड जो केन्द्र से होकर गुजरता है, उसेव्यास कहा जाता है।
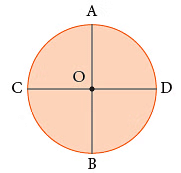 यहाँ, AB और CD वृत्त O के व्यास हैं।
यहाँ, AB और CD वृत्त O के व्यास हैं। - परिधि: वृत्त की सीमा की लंबाई को परिधि कहा जाता है।
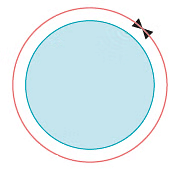
वृत्त का त्रिज्या और व्यास के बीच संबंध
दी गई आकृति में, AB वृत्त का व्यास है। AO और OB वृत्त की दो त्रिज्याएँ हैं।
OA, OB और AB को मापें। OA = ____ सेमी, OB = ____ सेमी, AB = ___ सेमी।
आप पाएंगे कि AB = 2OA या 2OB = 2 × त्रिज्या।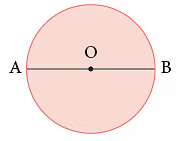
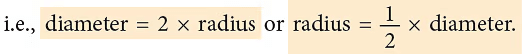 वृत्त का आंतरिक और बाह्य
वृत्त का आंतरिक और बाह्य
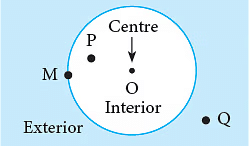
- बिंदु O और P वृत्त के आंतरिक हैं।
- बिंदु M वृत्त पर है.
- बिंदु Q वृत्त के bाह्य में है।
दी गई त्रिज्या वाला वृत्त बनाने के लिए
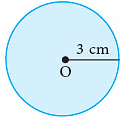
आपको साफ और सटीक वृत्त बनाने के लिए एक कंपास का उपयोग करना होगा। मान लीजिए, आपको 3 सेमी की त्रिज्या वाला वृत्त बनाना है। आप निम्नलिखित चरणों का पालन करके ऐसा कर सकते हैं।
चरण 1: अपनी रूलर की मदद से, कंपास की भुजाओं को 3 सेमी की लंबाई तक खोलें।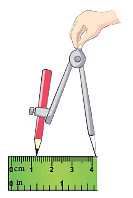
चरण 2: कागज पर कोई बिंदु O चिह्नित करें।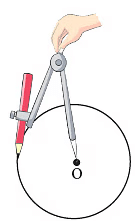 चरण 3: कंपास का स्टील वाला अंत चिह्नित O पर रखें। उपकरण के सिर को अंगूठे और तर्जनी के बीच पकड़े रखें ताकि कंपास का पेंसिल वाला अंत कागज को छू सके। अब, इसे पूरी तरह से घुमाएं ताकि पेंसिल वाला अंत वृत्त को ट्रेस कर सके। आपको O केंद्र के साथ 3 सेमी की त्रिज्या वाला वृत्त प्राप्त होगा।
चरण 3: कंपास का स्टील वाला अंत चिह्नित O पर रखें। उपकरण के सिर को अंगूठे और तर्जनी के बीच पकड़े रखें ताकि कंपास का पेंसिल वाला अंत कागज को छू सके। अब, इसे पूरी तरह से घुमाएं ताकि पेंसिल वाला अंत वृत्त को ट्रेस कर सके। आपको O केंद्र के साथ 3 सेमी की त्रिज्या वाला वृत्त प्राप्त होगा।
|
29 videos|73 docs|72 tests
|
FAQs on Notes: ज्यामिति - गणित और शिक्षाशास्त्र (Mathematics) CTET & TET Paper 1 - CTET & State TET
| 1. ज्यामिति में रेखा और रेखखंड में क्या अंतर है? |  |
| 2. कोण किसे कहते हैं और इसके प्रकार क्या हैं? |  |
| 3. रेखखंड की माप कैसे की जाती है? |  |
| 4. टैंग्राम क्या है और इसका उपयोग कैसे किया जाता है? |  |
| 5. क्षेत्रफल कैसे मापा जाता है? |  |




















