Notes: संख्या प्रणाली | गणित और शिक्षाशास्त्र (Mathematics) CTET & TET Paper 2 - CTET & State TET PDF Download
यह अध्याय CTET और राज्य TET परीक्षाओं के लिए महत्वपूर्ण है। इसमें संख्या प्रणाली, गणितीय क्रियाएँ, विभाजन परीक्षण, और भिन्नों जैसे महत्वपूर्ण विषयों को शामिल किया गया है। पिछले वर्षों के CTET और राज्य TET परीक्षा पत्रों का विश्लेषण करने से पता चलता है कि प्रत्येक परीक्षा में इस अध्याय से सामान्यतः 3 से 5 प्रश्न पूछे जाते हैं।
एक संख्या का प्रतिनिधित्व करने के लिए, हम गणित के दस विभिन्न मूल प्रतीकों का उपयोग करते हैं: 0, 1, 2, 3, 4, 5, 6, 7, 8, और 9। इन प्रतीकों को अंक कहा जाता है। इन अंकों का एक संयोजन जो एक संख्या का प्रतिनिधित्व करता है, उसे संख्यात्मक कहा जाता है।
नोट: किसी भी संख्या का प्रतिनिधित्व करने के लिए सभी अंकों का उपयोग करना जरूरी नहीं है। एक या अधिक अंक किसी संख्या का प्रतिनिधित्व करने के लिए उपयोग किए जा सकते हैं। उदाहरण के लिए: 11, 321, 333, 4978, 5521, आदि।
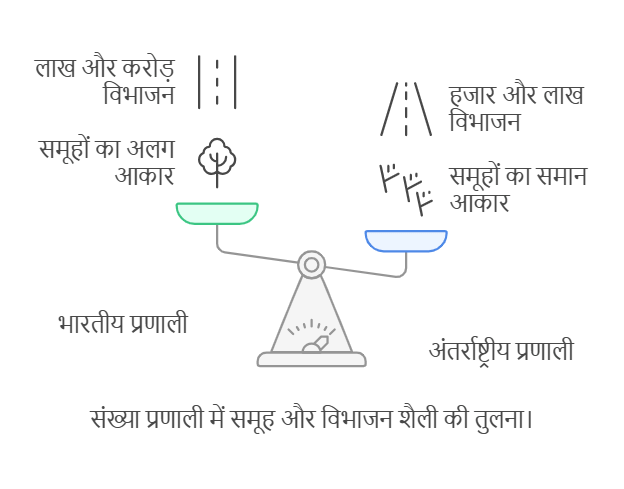
संख्या प्रणाली
संख्याओं के प्रतिनिधित्व के मुख्यतः दो प्रणाली हैं: भारतीय प्रणाली और अंतरराष्ट्रीय प्रणाली।
1. भारतीय (हिंदू-अरबी) प्रणाली
इस प्रणाली में, हम संख्या के अंकों को नीचे (एक) से लेकर ऊपर (करोड़) तक लिखते हैं। उदाहरण के लिए, संख्या 35,678,932 पर विचार करें।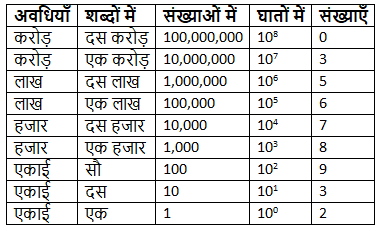
भारतीय प्रणाली के अनुसार, संख्या 35,678,932 को "तीन करोड़, पचपन लाख, सत्तावन हजार, नौ सौ बत्तीस\" के रूप में पढ़ा जाता है।
2. अंतर्राष्ट्रीय संख्या प्रणाली
अंतर्राष्ट्रीय प्रणाली में, हम एक संख्या के अंकों को नीचे (एकाई) से ऊपर (करोड़) तक लिखते हैं। उदाहरण के लिए, संख्या 35,678,932 पर विचार करें। इस संख्या का विभाजन निम्नलिखित है:
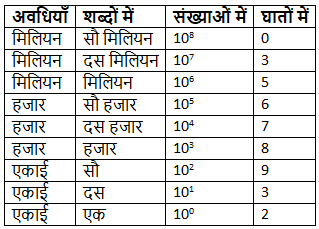
संख्या 35,678,932 को इस प्रकार पढ़ा जाता है: पैंतीस करोड़ छह लाख सत्तासी हजार नौ सौ बत्तीस।
उदाहरण
उदाहरण 1
निम्नलिखित संख्याओं को अंकों में परिवर्तित करें:
- तीन करोड़ चौबीस लाख एक हजार दस
- छह मिलियन सात हजार सत्ताईस
हल:
(i) 3 × 107 + 2 × 106 + 4 × 105 + 1 × 103 + 10 = 30,000,000 + 2,000,000 + 400,000 + 1,000 + 10 = 32,401,010
(ii) 6 × 106 + 8 × 103 + 3 × 101 + 7 = 6,000,000 + 8,000 + 30 + 7 = 6,008,037
उदाहरण 2
संख्या 865,421 को भारतीय और अंतर्राष्ट्रीय प्रणालियों में शब्द रूप में लिखें।
हल:
भारतीय प्रणाली: आठ लाख पैंसठ हजार चार सौ एक।
अंतर्राष्ट्रीय प्रणाली: आठ सौ पैंसठ हजार चार सौ एक।
संख्याओं में अंकों का चेहरा और स्थान मान
चेहरा मान: किसी संख्या में अंक का चेहरा मान, उस अंक का स्वयं का मान है, चाहे वह किसी भी स्थान पर हो। उदाहरण के लिए, संख्या 92,347 में, 9 का चेहरा मान 9 है, 2 का चेहरा मान 2 है, 3 का चेहरा मान 3 है, और इसी प्रकार।
स्थान मूल्य: एक अंक का स्थान मूल्य उस अंक की संख्या में स्थिति पर निर्भर करता है। इसे निम्नलिखित तरीके से गणना की जाती है:
- एकाई अंक = (एकाई अंक) × 100
- दशमलव अंक = (दशमलव अंक) × 101
- सौ अंक = (सौ अंक) × 102
- हजार अंक = (हजार अंक) × 103
उदाहरण के लिए, संख्या 4,354,972,375 में:
- 4 × 109 + 3 × 108 + 5 × 107 + 4 × 106 + 9 × 105 + 7 × 104 + 2 × 103 + 3 × 102 + 7 × 101 + 5 × 100
इस प्रकार, एक अंक का स्थान मूल्य उसकी स्थिति पर निर्भर करता है। उदाहरण के लिए, 5 का मुख्य मूल्य दोनों स्थानों में पाँच ही रहता है, लेकिन इसके स्थान मूल्य 5 और 50,000,000 हैं।
n-अंक के सबसे बड़े और सबसे छोटे नंबर
1. n-अंक का सबसे बड़ा नंबर
n-अंक का सबसे बड़ा नंबर उस अंक 9 को n के मान के अनुसार बार लिखकर बनाया जाता है।
उदाहरण के लिए, 5-अंक का सबसे बड़ा नंबर 99999 है।
2. n-अंक का सबसे छोटा नंबर
n-अंक का सबसे छोटा नंबर अंक 1 को लिखकर और उसके बाद (n-1) शून्य जोड़कर बनाया जाता है।
उदाहरण के लिए, 5-अंक का सबसे छोटा नंबर 10000 है।
उदाहरण
5-अंक के सबसे बड़े नंबर और 6-अंक के सबसे छोटे नंबर के बीच का अंतर क्या है?
- 1
- 9
- 11
- 99
समाधान:
5-अंक का सबसे बड़ा नंबर = 99999
6-अंक का सबसे छोटा नंबर = 100000
आवश्यक अंतर = 100000 - 99999 = 1
रोमन अंकों
जिन नंबरों का हम सामान्यतः उपयोग करते हैं (जैसे, 1, 2, 3, ...) उन्हें 'अरबी नंबर' कहा जाता है। कभी-कभी, हम एक और प्रणाली का उपयोग करते हैं जिसे रोमन प्रणाली कहा जाता है। रोमन अंक कभी-कभी कक्षा (जिसमें एक छात्र पढ़ाई करता है), एक उम्मीदवार की स्थिति, घड़ी के चेहरे, पृष्ठ संख्या आदि को प्रदर्शित करने के लिए उपयोग किए जाते हैं।
रोमन अंकों की तालिका
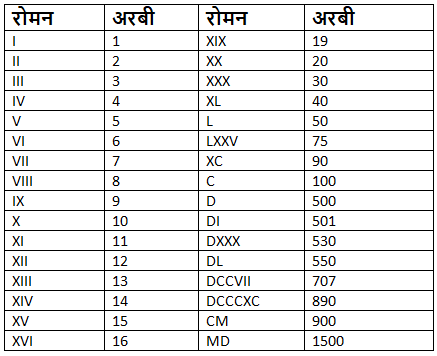
रोमन अंकों में प्रयुक्त अक्षर
- I = 1
- V = 5
- X = 10
- L = 50
- C = 100
- D = 500
- M = 1000
रोमन अंकों के लक्षण
- आम तौर पर, एक अक्षर को तीन बार से अधिक नहीं दोहराया जा सकता है। उदाहरण के लिए, I = 1, II = 2, III = 3, लेकिन 4 को IIII नहीं लिखा जाता; इसे IV के रूप में लिखा जाता है।
- रोमन अंकों के दोहराव में, रोमन अंक का मान व्यक्तिगत अंकों के मान का योग होता है। उदाहरण के लिए, III = 1 + 1 + 1 = 3, MM = 1000 + 1000 = 2000।
- V, L, और D को दोहराया नहीं जा सकता।
- I केवल V और X से घटाया जाता है; X केवल L, M, और C से घटाया जाता है; C केवल D और M से घटाया जाता है। V, L, और D को घटाया नहीं जाता।
- यदि एक छोटा रोमन प्रतीक एक बड़े प्रतीक के बाईं ओर है, तो संख्या का मान छोटे प्रतीक को बड़े प्रतीक से घटाकर निर्धारित किया जाता है। उदाहरण के लिए, XC = 100 - 10 = 90, CD = 500 - 100 = 400।
- यदि एक छोटा रोमन प्रतीक एक बड़े प्रतीक के दाईं ओर है, तो संख्या का मान दोनों प्रतीकों को जोड़कर निर्धारित किया जाता है। उदाहरण के लिए, XIII = 10 + 1 + 1 + 1 = 13, MD = 1000 + 500 = 1500।
- यदि किसी संख्या के ऊपर एक बार रखा जाता है, तो उसका मान 1000 गुना बढ़ जाता है। उदाहरण के लिए, IV = 4 × 1000 = 4000, D = 500 × 1000 = 500,000।
संख्याओं का वर्गीकरण
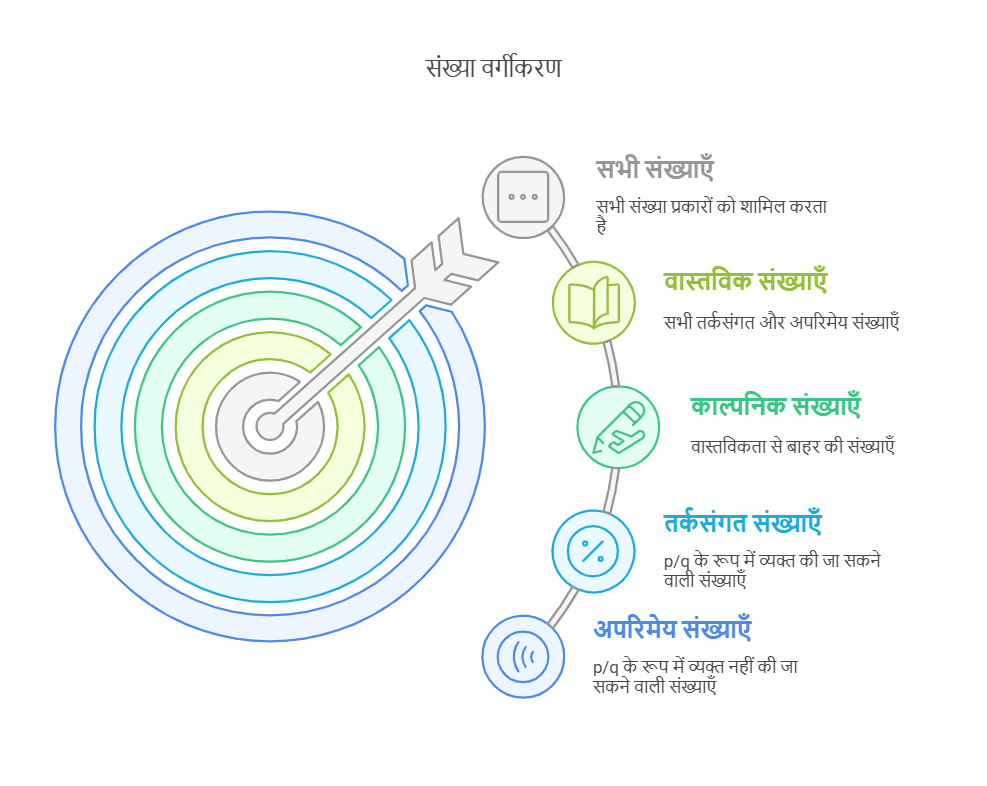
1. वास्तविक संख्याएँ
ऐसी संख्याएँ जो वर्ग करने पर सकारात्मक परिणाम देती हैं, उन्हें वास्तविक संख्याएँ कहा जाता है। इसमें सभी सकारात्मक, नकारात्मक, तर्कसंगत, और अपरिमेय संख्याएँ शामिल हैं। उदाहरण के लिए, 3 और √2 वास्तविक संख्याएँ हैं।
2. काल्पनिक संख्याएँ
जो संख्याएँ वास्तविक नहीं होती हैं, उन्हें काल्पनिक संख्याएँ कहा जाता है। जब इनका वर्ग किया जाता है, तो ये नकारात्मक मान देती हैं। उदाहरण के लिए, √-2 एक काल्पनिक संख्या है।
3. तर्कसंगत संख्याएँ (या भिन्न)
ऐसी संख्याएँ जिन्हें p/q के रूप में व्यक्त किया जा सकता है, जहाँ p और q पूर्णांक हैं और q ≠ 0, उन्हें तर्कसंगत संख्याएँ कहा जाता है। इन्हें Q द्वारा प्रदर्शित किया जाता है। उदाहरणों में 3/5, 4/9, और 2/7 शामिल हैं।
4. अपरिमेय संख्याएँ
ऐसी संख्याएँ जिन्हें p/q के रूप में व्यक्त नहीं किया जा सकता, उन्हें अपरिमेय संख्याएँ कहा जाता है। उदाहरणों में √2, √3, और √5 शामिल हैं।
5. प्राकृतिक संख्याएँ
1 से शुरू होने वाली सभी लगातार गिनती की संख्याएँ प्राकृतिक संख्याएँ कहलाती हैं। इन्हें N द्वारा प्रदर्शित किया जाता है। उदाहरणों में 1, 2, 3, 4 आदि शामिल हैं। ध्यान दें कि 0 एक प्राकृतिक संख्या नहीं है।
6. पूर्ण संख्याएँ
सभी प्राकृतिक संख्याएँ, जिसमें शून्य शामिल है, पूर्ण संख्याएँ कहलाती हैं। इन्हें W द्वारा प्रदर्शित किया जाता है। उदाहरणों में 0, 1, 2, 3 आदि शामिल हैं।
7. पूर्णांक
सभी सकारात्मक और नकारात्मक पूर्ण संख्याएँ पूर्णांक कहलाती हैं। इन्हें I द्वारा प्रदर्शित किया जाता है। उदाहरणों में ..., -3, -2, -1, 0, 1, 2, 3, ... शामिल हैं।
- सकारात्मक पूर्णांक: प्राकृतिक संख्याएँ सकारात्मक पूर्णांक कहलाती हैं। इन्हें I द्वारा प्रदर्शित किया जाता है। उदाहरणों में 1, 2, 3 आदि शामिल हैं।
- नकारात्मक पूर्णांक: प्राकृतिक संख्याओं का नकारात्मक रूप नकारात्मक पूर्णांक कहलाता है। इन्हें I- द्वारा प्रदर्शित किया जाता है। उदाहरणों में -1, -2, -3 आदि शामिल हैं।
- नोट: 0 न तो सकारात्मक है और न ही नकारात्मक पूर्णांक है।
8. सम संख्याएँ
ऐसी संख्या जो 2 से पूरी तरह विभाज्य होती है, उसे सम संख्या कहा जाता है। उदाहरणों में 8, 30, और 42 शामिल हैं। ध्यान दें कि हर सम संख्या का इकाई स्थान 0, 2, 4, 6, या 8 होगा।
9. विषम संख्या (Odd Numbers)
वे संख्याएँ जो 2 से विभाज्य नहीं होती हैं, उन्हें विषम संख्या कहा जाता है। उदाहरण हैं 1, 3, 5, 7, और 9।
10. अभाज्य संख्या (Prime Numbers)
एक गणना संख्या जो केवल 1 और स्वयं से ही विभाज्य होती है, उसे अभाज्य संख्या कहा जाता है। उदाहरण हैं 2, 3, 5, 7, 11, 13, 17, आदि। ध्यान दें कि 2 सबसे छोटी और एकमात्र सम अभाज्य संख्या है, और 1 एक अभाज्य संख्या नहीं है।
1 से 100 के बीच 25 अभाज्य संख्याएँ हैं: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, और 97।
अभाज्य संख्याओं की जांच (Test of Prime Numbers)
यह निर्धारित करने के लिए कि एक संख्या P अभाज्य है या नहीं:
- एक पूर्णांक x खोजें ताकि x² > P।
- x से कम या उसके बराबर सभी अभाज्य संख्याएँ लें।
- यदि इनमें से कोई भी अभाज्य संख्या P को ठीक से विभाजित नहीं करती है, तो P अभाज्य है। अन्यथा, P अभाज्य नहीं है।
11. समग्र संख्या (Composite Numbers)
एक समग्र संख्या में स्वयं और एक के अलावा अन्य गुणांक होते हैं, जिससे यह एक गैर-अभाज्य संख्या बन जाती है। उदाहरण हैं 4, 6, 9, 14, और 15। ध्यान दें कि 1 न तो अभाज्य है और न ही समग्र, और एक समग्र संख्या सम या विषम हो सकती है।
12. सह-प्राइम संख्या (Coprime Numbers)
दो प्राकृतिक संख्याएँ सह-प्राइम कहलाती हैं यदि उनके पास 1 के अलावा कोई सामान्य गुणांक नहीं होता। उदाहरण हैं (2, 5), (7, 15), और (9, 13)।
संख्याओं पर संचालन
संख्याओं पर विभिन्न संचालन में शामिल हैं:
1. जोड़ना
जब दो या अधिक संख्याएँ एक साथ मिलती हैं, तो इसे जोड़ना कहा जाता है, जिसे ‘ ’ चिह्न द्वारा दर्शाया जाता है। उदाहरण के लिए:
52 + 76 + 87 = 215
2. घटाना
जब एक या अधिक संख्याएँ एक बड़ी संख्या से निकाली जाती हैं, तो इसे घटाना कहा जाता है, जिसे ‘−’ चिह्न द्वारा दर्शाया जाता है। उदाहरण के लिए:
139 - 12 - 60 = 67
3. गुणा करना
जब दो संख्याएँ, जैसे x और y, एक साथ गुणा की जाती हैं, तो x को y बार जोड़ा जाता है या y को x बार जोड़ा जाता है। इसे ‘×’ चिह्न द्वारा दर्शाया जाता है। उदाहरण के लिए:
7 × 5 = 7 + 7 + 7 + 7 + 7 = 35
4. भाग करना
भाग करना उस तरीके को कहा जाता है जिससे यह पता लगाया जाता है कि एक दी गई संख्या, जिसे भाजक (divisor) कहा जाता है, कितनी बार दूसरी दी गई संख्या, जिसे भाज्य (dividend) कहा जाता है, में समाहित है। भागफल (quotient) परिणाम है, और भाज्य और भाजक तथा भागफल के गुणनफल के बीच का अंतर शेष (remainder) कहा जाता है। उदाहरण के लिए:
362 ÷ 39
भाजक ← 39) 362 (9 → भागफल
351
11 → शेष
ये मात्राएँ निम्नलिखित संबंध द्वारा आपस में संबंधित हैं:
भाज्य = (भाजक × भागफल) + शेष
उदाहरण 13
एक भागफल में, भागफल 97 है, शेष 105 है, और भाजक भागफल और शेष के योग के बराबर है। भाज्य क्या है?
- 22000
- 19699
- 19800
- 19700
समाधान: (2)
भाजक = 97 + 105 = 202
भाज्य = 202 × 97 + 105 = 19699
अतः, भाज्य 19699 है।
उदाहरण 14
दूसरे प्राकृतिक संख्या, दूसरे पूर्णांक, और दूसरे अभाज्य संख्या का गुणनफल ज्ञात करें।
- 0
- 4
- 6
- 7
समाधान: (3)
दूसरा प्राकृतिक संख्या = 2
दूसरा पूर्ण संख्या = 1
दूसरा प्राइम संख्या = 3
आवश्यक उत्पाद = 2 × 1 × 3 = 6
संख्याओं पर क्रियाओं के गुण
मान लें कि a और b दो संख्याएँ हैं। तब:
- जोड़ साम्यात्मक है: a + b = b + a
- उदाहरण के लिए: 930 + 56 = 986 और 56 + 930 = 986
- घटाना साम्यात्मक नहीं है: a - b ≠ b - a
- उदाहरण के लिए: 30 - 8 = 22 लेकिन 8 - 30 = -22
- गुणा साम्यात्मक है: a × b = b × a
- उदाहरण के लिए: 22 × 32 = 704 और 32 × 22 = 704
- भाग साम्यात्मक नहीं है: a ÷ b ≠ b ÷ a
- उदाहरण के लिए: 25 ÷ 5 = 5 लेकिन 5 ÷ 25 = 0.2
कुछ महत्वपूर्ण पद
- जोड़ने की पहचान: जब 0 (शून्य) को किसी भी संख्या में जोड़ा जाता है, तो हम वही संख्या प्राप्त करते हैं।
- किसी भी वास्तविक संख्या a के लिए: a + 0 = a इसलिए, 0 को a की जोड़ने की पहचान कहा जाता है।
- जोड़ने का व्युत्क्रम: वह संख्या जो, जब दी गई संख्या में जोड़ी जाती है, तो परिणाम शून्य होता है।
- किसी भी वास्तविक संख्या a के लिए: a + (-a) = 0 इसलिए, -a को a का जोड़ने का व्युत्क्रम कहा जाता है।
- गुणन की पहचान: जब 1 (एक) को किसी भी वास्तविक संख्या से गुणा किया जाता है, तो हमें वही संख्या प्राप्त होती है।
- किसी भी वास्तविक संख्या a के लिए: a × 1 = a इसलिए, 1 को a की गुणन की पहचान कहा जाता है।
- गुणन का व्युत्क्रम: वह संख्या जो, जब दी गई संख्या से गुणा की जाती है, तो परिणाम 1 होता है।
- किसी भी वास्तविक संख्या a के लिए: a × (1/a) = 1 इसलिए, 1/a को a का गुणन का व्युत्क्रम कहा जाता है। नोट: गुणन का व्युत्क्रम किसी संख्या का व्युत्क्रम के समान होता है।
- संयुक्त नियम: किसी भी तीन पूर्णांकों a, b, और c के लिए, नियम इस प्रकार परिभाषित है: (a + b) + c = a + (b + c) और (a × b) × c = a × (b × c)
- वितरण नियम: किसी भी तीन पूर्णांकों a, b, और c के लिए, नियम इस प्रकार परिभाषित है: a × (b + c) = (a × b) + (a × c)
उदाहरण 15
3 का जोड़ात्मक और गुणात्मक विपरीत ज्ञात करें।
- -3, 1/3
- -3, -3
- 3, 1
- इनमें से कोई नहीं
समाधान: (1)
जोड़ात्मक विपरीत: 3 + (-3) = 0, इसलिए -3, 3 का जोड़ात्मक विपरीत है।
गुणात्मक विपरीत: 3 × (1/3) = 1, इसलिए 1/3, 3 का गुणात्मक विपरीत है।
अनुमानित मान
कभी-कभी, हम विभिन्न परिस्थितियों में अनुमानित मानों का उपयोग करते हैं। उदाहरण के लिए, एक पार्टी में, हम मेहमानों की संख्या का अनुमान लगाते हैं। यदि एक व्यक्ति का एक महीने का व्यय ₹1976 है, तो इसे ₹2000 के रूप में अनुमानित किया जा सकता है।
नजदीकी दस के लिए अनुमानित करना
जब किसी संख्या को नजदीकी दस के लिए गोल किया जाता है:
- अंक का स्थान बदलकर 0 कर दें।
- यदि दस के स्थान पर अंक 5 या उससे अधिक है, तो दस के अंक को 1 से बढ़ाएं; अन्यथा, इसे अपरिवर्तित छोड़ दें।
उदाहरण के लिए:
- 542 का अनुमान 540 है।
- 7869 का अनुमान 7870 है।
नजदीकी सौ के लिए अनुमानित करना
जब किसी संख्या को नजदीकी सौ के लिए अनुमानित किया जाता है:
- एकाइ और десят के अंकों को 0 से बदलें।
- यदि मूल संख्या में दस का अंक 5 या उससे अधिक है, तो सौ के अंक को 1 से बढ़ाएं; अन्यथा, इसे अपरिवर्तित छोड़ दें।
उदाहरण के लिए:
- 5486 का अनुमान 5500 है।
- 89714 का अनुमान 89700 है।
हम हजार, दस हजार, आदि के लिए भी अनुमानित कर सकते हैं और योग, अंतर, गुणन और भागफल का अनुमान लगा सकते हैं।
उदाहरण 16
6285 + 13276 + 5217 का अनुमानित मान ज्ञात करें।
- 24900
- 24800
- 24850
- इनमें से कोई नहीं
समाधान: (2)
6285 का अनुमानित मान 6300 है।
13276 का अनुमानित मान 13300 है।
5217 का लगभग मान 5200 है।
इसलिए, लगभग योग = 6300 + 13300 + 5200 = 24800।
उदाहरण 17
22 × 77 का लगभग मान खोजें।
- 1600
- 1700
- 1650
- इनमें से कोई नहीं
समाधान: (1)
22 का लगभग मान 20 है।
77 का लगभग मान 80 है।
इसलिए, 22 × 77 का लगभग मान = 20 × 80 = 1600।
उदाहरण 18
9876321 का लगभग हजार खोजें।
- 9876321
- 9876000
- 987700
- इनमें से कोई नहीं
समाधान: (2)
9876321 का अनुमान = 9876000 है।
भाग्यता के परीक्षण
2 से भाग्यता
नियम: यदि किसी संख्या का अंतिम अंक सम या शून्य है, तो वह संख्या 2 से भाग्य है।
उदाहरण: 12, 86, 130, 568926, और 5983450 2 से भाग्य हैं।
3 से भाग्यता
नियम: यदि किसी संख्या के अंकों का योग 3 से भाग्य है, तो वह संख्या भी 3 से भाग्य है।
उदाहरण: 8349 → 8 + 3 + 4 + 9 = 24 (3 से भाग्य), इसलिए 8349 3 से भाग्य है।
4 से भाग्यता
नियम: यदि किसी संख्या के अंतिम दो अंक 4 से भाग्य हैं, तो वह संख्या 4 से भाग्य है।
उदाहरण: 324, 5632, 3500, 4320, 89412, 84300 4 से भाग्य हैं क्योंकि उनके अंतिम दो अंक 4 से भाग्य हैं।
5 से भाग्यता
नियम: यदि किसी संख्या का अंतिम अंक 5 या 0 है, तो वह संख्या 5 से भाग्य है।
उदाहरण: (i) 1345 → अंतिम अंक 5 है, इसलिए 5 से भाग्य है।
(ii) 1340 → अंतिम अंक 0 है, इसलिए 5 से भाग्य है।
6 से भाग्यता
नियम: एक संख्या 6 से भाग्य है यदि वह 2 और 3 दोनों से भाग्य है।
उदाहरण:
(i) 120 → अंतिम अंक 0 है और अंकों का योग (1 2 0 = 3) 3 से विभाज्य है, इसलिए 6 से विभाज्य है।
(ii) 1056 → अंतिम अंक सम (6) है और अंकों का योग (1 0 5 6 = 12) 3 से विभाज्य है, इसलिए 6 से विभाज्य है।
7 द्वारा विभाज्यता
नियम: यदि इकाई अंक का दो गुना और अन्य अंकों द्वारा बने संख्या का अंतर 0 या 7 का गुणांक है, तो संख्या 7 से विभाज्य है।
उदाहरण: 581 → 58 - 2*1 = 56 (7 से विभाज्य), इसलिए 581 भी 7 से विभाज्य है।
8 द्वारा विभाज्यता
नियम: यदि किसी संख्या के अंतिम तीन अंक 8 से विभाज्य हैं, तो पूरी संख्या भी 8 से विभाज्य है।
उदाहरण: (i) 3648 → अंतिम तीन अंक 648, 8 से विभाज्य हैं, इसलिए 8 से भी विभाज्य है।
(ii) 2880 → अंतिम तीन अंक 880, 8 से विभाज्य हैं, इसलिए 8 से भी विभाज्य है।
(iii) 216000 → अंतिम तीन अंक 000 हैं, इसलिए 8 से भी विभाज्य है।
9 द्वारा विभाज्यता
नियम: यदि किसी संख्या के सभी अंकों का योग 9 से विभाज्य है, तो संख्या भी 9 से विभाज्य है।
उदाहरण: (i) 39681 → 3 9 6 8 1 = 27 (9 से विभाज्य), इसलिए 39681 भी 9 से विभाज्य है।
(ii) 456138 → 4 5 6 1 3 8 = 27 (9 से विभाज्य), इसलिए 456138 भी 9 से विभाज्य है।
10 द्वारा विभाज्यता
नियम: कोई भी संख्या जो शून्य या एक से अधिक शून्य से समाप्त होती है, 10 से विभाज्य होती है।
उदाहरण: 150, 7250, 1900, 35450, आदि 10 से विभाज्य हैं।
11 द्वारा विभाज्यता
नियम: यदि विषम और सम स्थानों पर अंकों के योग का अंतर 0 या 11 से विभाज्य है, तो संख्या 11 से विभाज्य है।
उदाहरण: (i) 3245682 → विषम स्थान का योग (3 4 6 2) = 15 और सम स्थान का योग (2 5 8) = 15, इसलिए 11 से विभाज्य है।
(ii) 283712 → विषम स्थान का योग (2 3 1) = 6 और सम स्थान का योग (8 7 2) = 17, जो 11 के बराबर है, इसलिए 11 से विभाज्य है।
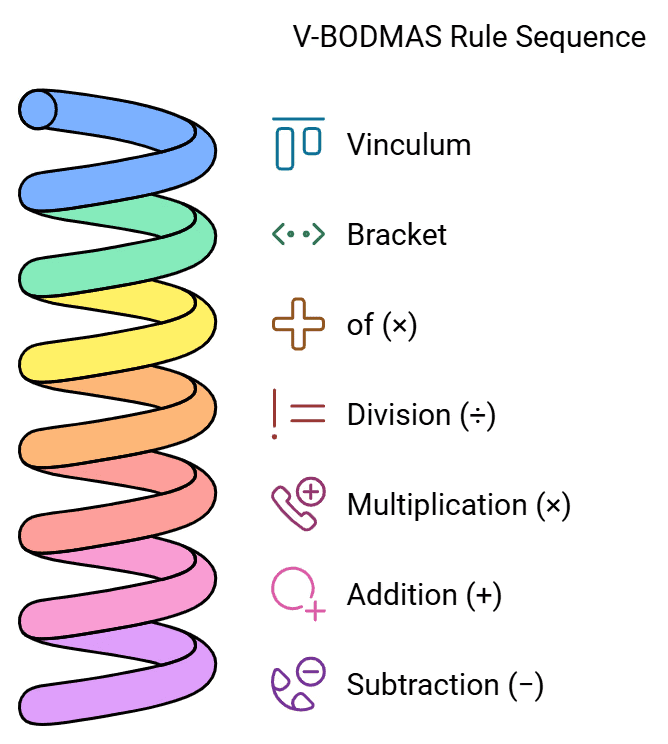
V-BODMAS नियम
किसी संख्यात्मक अभिव्यक्ति को सरल बनाने के लिए जिसमें जोड़, घटाव, गुणा, भाग, और कोष्ठक जैसी विभिन्न क्रियाएँ शामिल होती हैं, एक विशेष क्रम का पालन करना आवश्यक है, जिसे V-BODMAS के संक्षिप्त नाम से जाना जाता है:
- V → विंकुलम (संख्याओं के समूह पर खींची गई क्षैतिज रेखा या बार '−')
- B → कोष्ठक
- O → गुणन (×)
- D → भाग (÷)
- M → गुणन (×)
- A → जोड़ ( )
- S → घटाव (−)
महत्वपूर्ण नोट्स:
- ‘Of’ का अर्थ गुणन है और इसे भाग से पहले किया जाता है।
- कोष्ठकों का क्रम निम्नलिखित प्रकार से निष्पादित किया जाना चाहिए:
- Vi → विंकुलम या बार ‘−’
- Ci → गोल कोष्ठक ()
- Cu → कर्ली कोष्ठक {}
- Sq → स्क्वायर कोष्ठक []
उदाहरण 22
225 ÷ 5 of 3 17 − 8 × 12 ÷ 6 का मान ज्ञात करें:
- 12
- 16
- 14
- 6
समाधान: (2)
पहले, गुणन ('of') करें: 225 ÷ 15 17 − 8 × 12 ÷ 6
फिर, भाग करें: 15 17 − 8 × 12 ÷ 6
गुणन: 15 17 − 96 ÷ 6
भाग: 15 17 − 16
जिसका परिणाम: 16
उदाहरण 23
यदि ‘−’ का अर्थ ‘ ’, ‘×’ का अर्थ ‘−’, ‘÷’ का अर्थ ‘×’, और ‘ ’ का अर्थ ‘÷’ है, तो ‘20 − 8 × 3 ÷ 18 9’ का मान ज्ञात करें।
- 25
- 24
- 22
- 23
समाधान: (3)
दी गई प्रतिस्थापनों के अनुसार: 20 8 − 3 × 18 ÷ 9
गुणन करें: 20 8 − 54 ÷ 9
भाग करें: 20 8 − 6
जिसका परिणाम: 22
महत्वपूर्ण पहचान
कुछ महत्वपूर्ण पहचान जो सरलीकरण के लिए उपयोग की जाती हैं, नीचे दी गई हैं:
- (a2 b2) = (a b)2 - 2ab
- (a - b)2 = a2 - 2ab + b2
- a2 - b2 = (a + b)(a - b)
- (a b c)2 = a2 b2 c2 + 2(ab + bc + ca)
- (a b)3 = a3 + b3 + 3ab(a + b)
- a3 b3 = (a + b)(a2 - ab + b2)
- a3 - b3 = (a - b)(a2 + ab + b2)
- (a b c)3 = a3 + b3 + c3 - 3(a b)(b c)(c a)
- यदि a b c = 0, तो a3 b3 c3 = 3abc
- (a b c)2 = a2 b2 c2 + 2(ab + bc + ca)
- (a b c)3 = a3 + b3 + c3 - 3(a b)(b c)(c a)
दो अंकीय संख्या और अंकगणितीय श्रृंखला
10 से 99 तक प्रत्येक संख्या एक दो अंकीय संख्या है। बाईं ओर का अंक दशम स्थान पर है और दाईं ओर का अंक एकम स्थान पर है। एक दो अंकीय संख्या प्राप्त करने के लिए, दशम स्थान के अंक को 10 से गुणा किया जाता है और एकम स्थान के अंक में जोड़ा जाता है। प्राप्त योग आवश्यक दो अंकीय संख्या होगी।
उदाहरण के लिए, यदि एकम स्थान का अंक 3 है और दशम स्थान का अंक 4 है, तो आवश्यक संख्या होगी:
4 × 10 + 3 = 40 + 3 = 43
उदाहरण 24
एक दो अंकीय संख्या के अंकों का योग 13 है। यदि इस संख्या के अंकों को उलटा किया जाता है, तो नई संख्या मूल संख्या से 9 कम होगी। मूल संख्या ज्ञात करें।
- 67
- 76
- 72
- 65
समाधान: (2)
अंकों का योग: (x + y = 13) …(i)
नई संख्या: (10y + x)
प्रश्न के अनुसार:
(10x + y - (10y + x) = 9)
(9x - 9y = 9)
(x - y = 1) …(ii)
समीकरण (i) और (ii) को हल करते हुए:
समीकरण (i) से, (x = 7)
समिकरण (ii) से, (y = 6)
इसलिए, आवश्यक संख्या है ( 10 times 7 + 6 = 76 )।
संख्याओं की अंकगणितीय श्रृंखला
कभी-कभी, दो निरंतर पदों के बीच का अंतर स्थिर होता है, इस स्थिति में श्रृंखला को अंकगणितीय श्रृंखला कहा जाता है।
मान लें कि श्रृंखला है (a, a d, a 2d, a 3d, ...)।
यहां, (a) पहला पद है और (d) सामान्य अंतर है।
इस श्रृंखला का (n)-वां पद है (Tn = a (n-1)d)।
इस श्रृंखला के पहले (n) पदों का योग है।
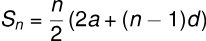
|
50 videos|152 docs|70 tests
|
















