तर्कसंगत संख्याएँ NCERT Solutions | गणित और शिक्षाशास्त्र (Mathematics) CTET & TET Paper 2 - CTET & State TET PDF Download
अभ्यास 8.1
प्रश्न 1: बीच की पाँच परिमेय संख्याएँ सूचीबद्ध करें:
(i) -1 और 0
उत्तर: आइए -1 और 0 को हर 6 वाली परिमेय संख्याओं के रूप में लिखें।
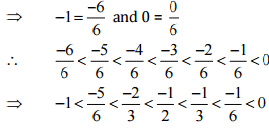 इसलिए, -1 और 0 के बीच पाँच परिमेय संख्याएँ होंगी
इसलिए, -1 और 0 के बीच पाँच परिमेय संख्याएँ होंगी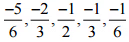
(ii) -2 और -1
उत्तर: आइए -2 और -1 को हर 6 वाली परिमेय संख्याओं के रूप में लिखें।
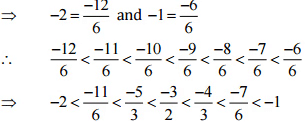 इसलिए, -2 और -1 के बीच पाँच परिमेय संख्याएँ होंगी
इसलिए, -2 और -1 के बीच पाँच परिमेय संख्याएँ होंगी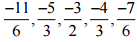
(iii) 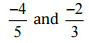 उत्तर:
उत्तर: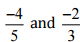 आइए हम समान हर वाली परिमेय संख्याओं के रूप में लिखें ।
आइए हम समान हर वाली परिमेय संख्याओं के रूप में लिखें ।
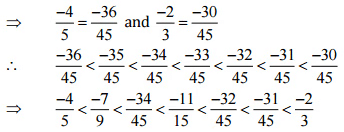 इसलिए, बीच में पाँच परिमेय संख्याएँ
इसलिए, बीच में पाँच परिमेय संख्याएँ 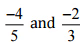 होंगी
होंगी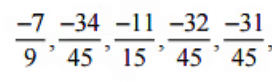
(iv) 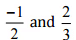 उत्तर:
उत्तर: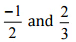 आइए हम समान हर वाली परिमेय संख्याओं के रूप में लिखें ।
आइए हम समान हर वाली परिमेय संख्याओं के रूप में लिखें ।
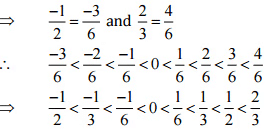 इसलिए, बीच में पाँच परिमेय संख्याएँ
इसलिए, बीच में पाँच परिमेय संख्याएँ 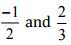 होंगी
होंगी 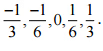
प्रश्न 2: निम्नलिखित प्रत्येक पैटर्न में चार और परिमेय संख्याएँ लिखिए:
(i) 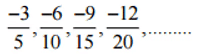 उत्तर:
उत्तर: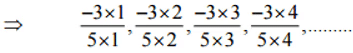 इसलिए, इस पैटर्न की अगली चार परिमेय संख्याएँ होंगी
इसलिए, इस पैटर्न की अगली चार परिमेय संख्याएँ होंगी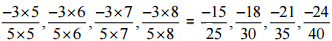
(ii) 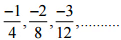 उत्तर:
उत्तर: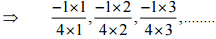 इसलिए, इस पैटर्न की अगली चार परिमेय संख्याएँ होंगी
इसलिए, इस पैटर्न की अगली चार परिमेय संख्याएँ होंगी
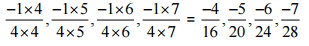
(iii) 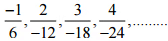 उत्तर:
उत्तर:
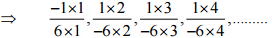 इसलिए, इस पैटर्न की अगली चार परिमेय संख्याएँ होंगी
इसलिए, इस पैटर्न की अगली चार परिमेय संख्याएँ होंगी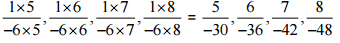
(iv) 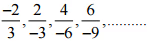 उत्तर:
उत्तर: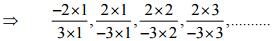 इसलिए, टिन के पैटर्न की अगली चार परिमेय संख्याएँ होंगी
इसलिए, टिन के पैटर्न की अगली चार परिमेय संख्याएँ होंगी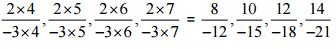
प्रश्न 3: चार परिमेय संख्याएँ दीजिए जो इसके समतुल्य हों:
(i) -2/7
उत्तर: -2/7 के समतुल्य चार परिमेय संख्याएँ हैं,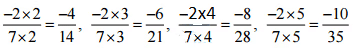
इसलिए, चार समतुल्य परिमेय संख्याएँ हैं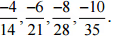
(ii) 5/-3
उत्तर: 5/-3 के समतुल्य चार परिमेय संख्याएँ हैं,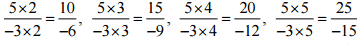
इसलिए, चार समतुल्य परिमेय संख्याएँ हैं 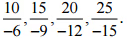
(iii) 4/9
उत्तर: 5/-3 के समतुल्य चार परिमेय संख्याएँ हैं,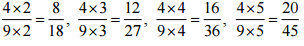
इसलिए, चार समतुल्य परिमेय संख्याएँ हैं 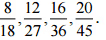
प्रश्न 4: संख्या रेखा खींचें और उस पर निम्नलिखित परिमेय संख्याओं को निरूपित करें:
(i) 3/4
उत्तर: हम जानते हैं कि 3/4, 0 से बड़ा और 1 से छोटा है।
∴ यह 0 और 1 के बीच में स्थित है। इसे संख्या रेखा पर इस प्रकार दर्शाया जा सकता है,
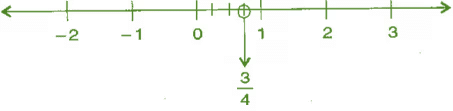
(ii) -5/8
उत्तर: हम जानते हैं कि -5/8, 0 से छोटा और -1 से बड़ा है।
∴ यह 0 और -1 के बीच में स्थित है। इसे संख्या रेखा पर इस प्रकार दर्शाया जा सकता है,
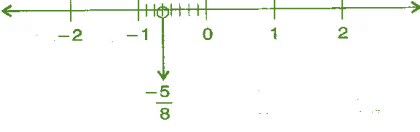
(iii) -7/4
उत्तर: अब उपरोक्त प्रश्न को इस प्रकार लिखा जा सकता है,
= (-7/4) = 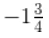 हम जानते हैं कि (-7/4), -1 से छोटा तथा -2 से बड़ा है।∴ यह -1 तथा -2 के बीच में स्थित है। इसे संख्या रेखा पर इस प्रकार दर्शाया जा सकता है,
हम जानते हैं कि (-7/4), -1 से छोटा तथा -2 से बड़ा है।∴ यह -1 तथा -2 के बीच में स्थित है। इसे संख्या रेखा पर इस प्रकार दर्शाया जा सकता है,
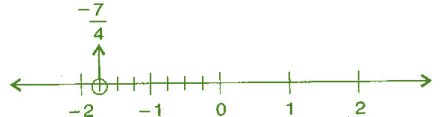
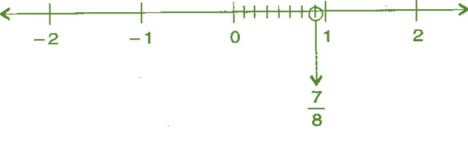
(iv) 7/8
उत्तर: हम जानते हैं कि 7/8, 0 से बड़ा और 1 से छोटा है।
∴ यह 0 और 1 के बीच में स्थित है। इसे संख्या रेखा पर इस प्रकार दर्शाया जा सकता है,
प्रश्न 5: संख्या रेखा पर बिंदु P, Q, R, S, T, U, A और B इस प्रकार हैं कि, TR = RS = SU और AP = PQ = QB। P, Q, R और S द्वारा दर्शाई गई परिमेय संख्याओं के नाम बताइए। 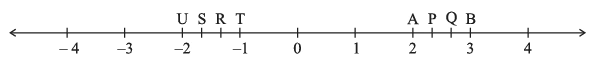
उत्तर:

प्रश्न 6: निम्नलिखित में से कौन सा युग्म समान परिमेय संख्याओं को दर्शाता है:
(i) 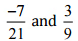 उत्तर: हमें यह जाँचना है कि दिया गया युग्म समान परिमेय संख्याओं को दर्शाता है।
उत्तर: हमें यह जाँचना है कि दिया गया युग्म समान परिमेय संख्याओं को दर्शाता है।
फिर,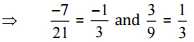 [सबसे कम पद में परिवर्तित करते हुए]
[सबसे कम पद में परिवर्तित करते हुए]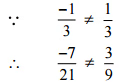 इसलिए, दिया गया युग्म समान परिमेय संख्याओं को नहीं दर्शाता है।
इसलिए, दिया गया युग्म समान परिमेय संख्याओं को नहीं दर्शाता है।
(ii) 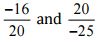 उत्तर: हमें यह जाँचना है कि दिया गया युग्म एक ही परिमेय संख्या को दर्शाता है
उत्तर: हमें यह जाँचना है कि दिया गया युग्म एक ही परिमेय संख्या को दर्शाता है
।
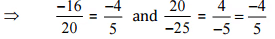 [न्यूनतम पद में परिवर्तित करना]
[न्यूनतम पद में परिवर्तित करना]
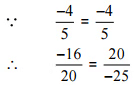 अतः दिया गया युग्म एक ही परिमेय संख्या को दर्शाता है।
अतः दिया गया युग्म एक ही परिमेय संख्या को दर्शाता है।
(iii) 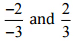 उत्तर: हमें यह जाँचना है कि दिया गया युग्म एक ही परिमेय संख्या को दर्शाता है
उत्तर: हमें यह जाँचना है कि दिया गया युग्म एक ही परिमेय संख्या को दर्शाता है
।
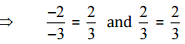 [न्यूनतम पद में परिवर्तित करना]
[न्यूनतम पद में परिवर्तित करना]
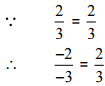 अतः दिया गया युग्म एक ही परिमेय संख्या को दर्शाता है।
अतः दिया गया युग्म एक ही परिमेय संख्या को दर्शाता है।
(iv) 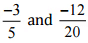 उत्तर: हमें यह जाँचना है कि दिया गया युग्म एक ही परिमेय संख्या को दर्शाता है
उत्तर: हमें यह जाँचना है कि दिया गया युग्म एक ही परिमेय संख्या को दर्शाता है
।
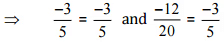 [न्यूनतम पद में परिवर्तित करना]
[न्यूनतम पद में परिवर्तित करना]
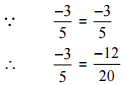 अतः दिया गया युग्म एक ही परिमेय संख्या को दर्शाता है।
अतः दिया गया युग्म एक ही परिमेय संख्या को दर्शाता है।
(v) 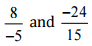 उत्तर: हमें यह जाँचना है कि दिया गया युग्म एक ही परिमेय संख्या को दर्शाता है
उत्तर: हमें यह जाँचना है कि दिया गया युग्म एक ही परिमेय संख्या को दर्शाता है
।
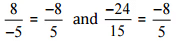 [न्यूनतम पद में परिवर्तित करना]
[न्यूनतम पद में परिवर्तित करना]
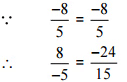 अतः दिया गया युग्म एक ही परिमेय संख्या को दर्शाता है।
अतः दिया गया युग्म एक ही परिमेय संख्या को दर्शाता है।
(vi) 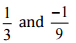 उत्तर: हमें यह जाँचना है कि दिया गया युग्म एक ही परिमेय संख्या को दर्शाता है
उत्तर: हमें यह जाँचना है कि दिया गया युग्म एक ही परिमेय संख्या को दर्शाता है
।
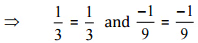 [न्यूनतम पद में परिवर्तित करना]
[न्यूनतम पद में परिवर्तित करना]
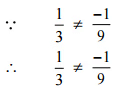 अतः, दिया गया युग्म समान परिमेय संख्या का प्रतिनिधित्व नहीं करता है।
अतः, दिया गया युग्म समान परिमेय संख्या का प्रतिनिधित्व नहीं करता है।
(vii) 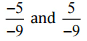 उत्तर: हमें यह जाँचना है कि दिया गया युग्म समान परिमेय संख्या को दर्शाता है या नहीं।
उत्तर: हमें यह जाँचना है कि दिया गया युग्म समान परिमेय संख्या को दर्शाता है या नहीं।
फिर,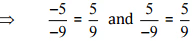 [सबसे कम टेरा में परिवर्तित करना]
[सबसे कम टेरा में परिवर्तित करना]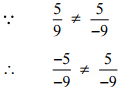 इसलिए, दिया गया युग्म समान परिमेय संख्या को नहीं दर्शाता है।
इसलिए, दिया गया युग्म समान परिमेय संख्या को नहीं दर्शाता है।
प्रश्न 7: निम्नलिखित परिमेय संख्याओं को सरलतम रूप में पुनः लिखें:
(i) -8/6
उत्तर: दी गई परिमेय संख्याओं को और सरल किया जा सकता है,
तब,
= -4/3 … [∵ अंश और हर दोनों को 2 से भाग दें]
(ii) 25/45
उत्तर: दी गई परिमेय संख्याओं को और सरल किया जा सकता है,
तब,
= 5/9 … [∵ अंश और हर दोनों को 5 से भाग दें]
(iii) -44/72
उत्तर: दी गई परिमेय संख्याओं को और सरल किया जा सकता है,
तब,
= -11/18 … [∵ अंश और हर दोनों को 4 से भाग दें]
(iv) -8/10
उत्तर: दी गई परिमेय संख्याओं को और सरल किया जा सकता है,
तब,
= -4/5 … [∵ अंश और हर दोनों को 2 से भाग दें]
प्रश्न 8: <, > और = में से सही प्रतीक वाले बॉक्स भरें:
(i)  उत्तर: हर 7 और 3 का LCM 21 है
उत्तर: हर 7 और 3 का LCM 21 है
∴ (-5/7) = [(-5 × 3)/ (7 × 3)] = (-15/21)
और (2/3) = [(2 × 7)/ (3 × 7)] = (14/21)
अब, -15 < 14
तो,
(-15/21) < (14/21)
इसलिए, -5/7 [<] 2/3
(ii) 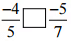 उत्तर: हर 5 और 7 का LCM 35 है
उत्तर: हर 5 और 7 का LCM 35 है
∴ (-4/5) = [(-4 × 7)/ (5 × 7)] = (-28/35)
और (-5/7) = [(-5 × 5)/ (7 × 5)] = (-25/35)
अब, -28 < -25
तो,
(-28/35) < (- 25/35)
इसलिए, -4/5 [<] -5/7
(iii) 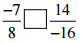 उत्तर: 14/-16 को और सरल किया जा सकता है,तब,
उत्तर: 14/-16 को और सरल किया जा सकता है,तब,
7/-8 … [∵ अंश और हर दोनों को 2 से भाग दें]
अतः,
(-7/8) = (-7/8)
अतः, -7/8 [=] 14/-16
(iv) 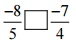 उत्तर: हर 5 और 4 का LCM 20 है
उत्तर: हर 5 और 4 का LCM 20 है
∴ (-8/5) = [(-8 × 4)/ (5 × 4)] = (-32/20)
और (-7/4) = [(-7 × 5)/ (4 × 5)] = (-35/20)
अब, -32 > – 35
तो,
(-32/20) > (- 35/20)
अतः, -8/5 [>] -7/4
(v) 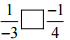 उत्तर: हर 3 और 4 का LCM 12 है
उत्तर: हर 3 और 4 का LCM 12 है
∴ (-1/3) = [(-1 × 4)/ (3 × 4)] = (-4/12)
और (-1/4) = [(-1 × 3)/ (4 × 3)] = (-3/12)
अब, -4 < – 3
तो,
(-4/12) < (- 3/12)
इसलिए, 1/-3 [<] -1/4
(vi) 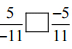 उत्तर: चूँकि, (-5/11) = (-5/11)
उत्तर: चूँकि, (-5/11) = (-5/11)
अतः, 5/-11 [=] -5/11
(vii) 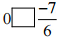 उत्तर: चूँकि प्रत्येक ऋणात्मक परिमेय संख्या 0 से छोटी होती है, इसलिए
उत्तर: चूँकि प्रत्येक ऋणात्मक परिमेय संख्या 0 से छोटी होती है, इसलिए
हमारे पास है:
= 0 [>] -7/6
प्रश्न 9: निम्नलिखित में से प्रत्येक में कौन बड़ा है:
(i) 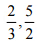 उत्तर: हर 3 और 2 का एल.सी.एम. 6 है
उत्तर: हर 3 और 2 का एल.सी.एम. 6 है
(2/3) = [(2 × 2)/ (3 × 2)] = (4/6)
और (5/2) = [(5 × 3)/ (2 × 3)] = (15/6)
अब, 4 < 15
तो, (4/6) < (15/6)
∴ 2/3 < 5/2
इसलिए, 5/2 बड़ा है।
(ii) 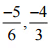
उत्तर: हर 6 और 3 का एल.सी.एम. 6 है
∴ (-5/6) = [(-5 × 1)/ (6 × 1)] = (-5/6)
और (-4/3) = [(-4 × 2)/ (3 × 2)] = (-12/6)
अब, -5 > -12
तो, (-5/6) > (- 12/6)
∴ -5/6 > -12/6
अतः, -5/6 बड़ा है।
(iii) 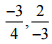
उत्तर: हर 4 और 3 का LCM 12 है
∴ (-3/4) = [(-3 × 3)/ (4 × 3)] = (-9/12)
और (-2/3) = [(-2 × 4)/ (3 × 4)] = (-8/12)
अब, -9 < -8 तो, (-9/12) < (- 8/12)
∴ -3/4 < 2/-3
इसलिए, 2/-3 बड़ा है।
(iv) 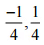
उत्तर: दी गई भिन्न घर्षण के समान है,
अतः -¼ < ¼
अतः ¼ बड़ा है,
(v) 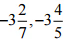
उत्तर: सबसे पहले हमें मिश्रित भिन्नों को अनुचित भिन्नों में बदलना होगा,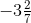 = -23/7
= -23/7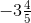 = -19/5तब, हर 7 और 5 का LCM 35 है∴ (-23/7) = [(-23 × 5)/ (7 × 5)] = (-115/35)
= -19/5तब, हर 7 और 5 का LCM 35 है∴ (-23/7) = [(-23 × 5)/ (7 × 5)] = (-115/35)
और (-19/5) = [(-19 × 7)/ (5 × 7)] = (-133/35)
अब, -115 > -133 तो, (-115/35) > (- 133/35)
∴ 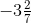 >
> 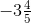 इसलिए,
इसलिए, 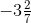 बड़ा है।
बड़ा है।
प्रश्न 10: निम्नलिखित परिमेय संख्याओं को आरोही क्रम में लिखिए:
(i) -3/5, -2/5, -1/5
उत्तर: दी गई परिमेय संख्याएँ समान भिन्नों के रूप में हैं,
अतः, (-3/5)< (-2/5) < (-1/5)
(ii) -1/3, -2/9, -4/3
उत्तर: दी गई परिमेय संख्याओं को समान भिन्नों में बदलने के लिए हमें LCM ज्ञात करना होगा,
3, 9 और 3 का LCM 9 है
अब,
(-1/3) = [(-1 × 3)/ (3 × 9)] = (-3/9)
(-2/9)= [(-2 × 1)/ (9 × 1)] = (-2/9)
(-4/3)= [(-4 × 3)/ (3 × 3)] = (-12/9)
स्पष्टतः, (-12/9) < (-3/9) < (-2/9)
अतः, (-4/3) < (-1/3) < (-2/9)
(iii) -3/7, -3/2, -3/4
उत्तर: दी गई परिमेय संख्याओं को समान भिन्नों में बदलने के लिए हमें LCM ज्ञात करना होगा,
7, 2 और 4 का LCM 28 है
अब, (-3/7)= [(-3 × 4)/ (7 × 4)] = (-12/28)
(-3/2)= [(-3 × 14)/ (2 × 14)] = (-42/28)
(-3/4)= [(-3 × 7)/ (4 × 7)] = (-21/28)
स्पष्टतः, (-42/28) < (-21/28) < (-12/28)
अतः, (-3/2) < (-3/4) < (-3/7)
अभ्यास 8.2
प्रश्न 1: योगफल ज्ञात कीजिए:
(i) 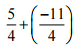
उत्तर: हमारे पास है:
= (5/4) – (11/4) = [(5 – 11)/4] … [∵ दोनों परिमेय संख्याओं में हर समान है]
= (-6/4)
= -3/2 … [∵ अंश और हर दोनों को 3 से विभाजित करें]
(ii) 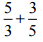
उत्तर: दी गई परिमेय संख्याओं के हरों का LCM लें।
3 और 5 का LCM 15 है। दी गई प्रत्येक परिमेय संख्या को उपरोक्त LCM के समान हर के रूप में व्यक्त करें।
अब, (5/3) = [(5 × 5)/ (3 × 5)] = (25/15)
(3/5) = [(3 × 3)/ (5 × 3)] = (9/15)
तो,
= (25/15) + (9/15) … [∵ दोनों परिमेय संख्याओं में हर समान है]
= (25 + 9)/15 = 34/15
(iii) 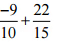
उत्तर: दी गई परिमेय संख्याओं के हरों का LCM लें।
10 और 15 का LCM 30 है। दी गई प्रत्येक परिमेय संख्या को उपरोक्त LCM के समान हर के रूप में व्यक्त करें।
अब,
(-9/10)= [(-9 × 3)/ (10 × 3)] = (-27/30)
(22/15)= [(22 × 2) / (15 × 2)] = (44/30)
तब, = (-27/30) + (44/30) … [∵ दोनों परिमेय संख्याओं में हर समान है]
= (-27 + 44)/30
= (17/30)
(iv) 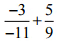
उत्तर: हमारे पास है, = 3/11 + 5/9
दी गई परिमेय संख्याओं के हरों का LCM लें।
11 और 9 का LCM 99 है।
दी गई प्रत्येक परिमेय संख्या को उपरोक्त LCM के समान हर के रूप में व्यक्त करें।
अब,
(3/11) = [(3 × 9)/ (11 × 9)] = (27/99)
(5/9) = [(5 × 11)/ (9 × 11)] = (55/99)
तब,
= (27/99) + (55/99) … [∵ दोनों परिमेय संख्याओं में हर समान है]
= (27 + 55)/99
= (82/99)
(v) 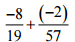
उत्तर: हमारे पास है = -8/19 – 2/57
दी गई परिमेय संख्याओं के हरों का LCM लें।
19 और 57 का LCM 57 है
प्रत्येक परिमेय संख्या को उपरोक्त LCM के साथ सामान्य हर के रूप में व्यक्त करें।
अब,
(-8/19)= [(-8 × 3)/ (19 × 3)] = (-24/57) (-2/57)= [(-2 × 1)/ (57 × 1)] = (-2/57)
तब,
= (-24/57) – (2/57) … [∵ दोनों परिमेय संख्याओं में हर समान है]
= (-24 – 2)/57 = (-26/57)
(vi) 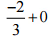
उत्तर: हम जानते हैं कि शून्य में कोई भी संख्या या भिन्न जोड़ने पर उत्तर वही संख्या या भिन्न होगी।
अतः
= -2/3 + 0
= -2/3
(vii) 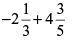
उत्तर: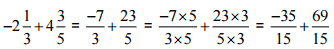 [3 और 5 का एल.सी.एम. 15 है]
[3 और 5 का एल.सी.एम. 15 है]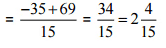
प्रश्न 2: ज्ञात करें:
(i) 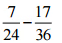
उत्तर: दी गई परिमेय संख्याओं के हरों का LCM लें।
24 और 36 का LCM 72 है।
दी गई प्रत्येक परिमेय संख्या को उपरोक्त LCM के उभयनिष्ठ हर के रूप में व्यक्त करें।
अब,
(7/24)= [(7 × 3)/ (24 × 3)] = (21/72)
(17/36)= [(17 × 2)/ (36 × 2)] = (34/72)
तब,
= (21/72) – (34/72) … [∵ दोनों परिमेय संख्याओं में हर समान है]
= (21 – 34)/72 = (-13/72)
(ii) 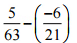
उत्तर: हम -6/21 = -2/7
= 5/63 – (-2/7) भी लिख सकते हैं
। हमारे पास है, = 5/63 + 2/7
दी गई परिमेय संख्याओं के हरों का LCM लें।
63 और 7 का LCM 63 है।
दी गई प्रत्येक परिमेय संख्या को उपरोक्त LCM के उभयनिष्ठ हर के रूप में व्यक्त करें।
अब,
(5/63)= [(5 × 1)/ (63 × 1)] = (5/63)
(2/7)= [(2 × 9)/ (7 × 9)] = (18/63)
तब, = (5/63) + (18/63) … [∵ दोनों परिमेय संख्याओं में हर समान है]
= (5 + 18)/63 = 23/63
(iii) 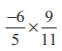
उत्तर: हमारे पास है, = -6/13 + 7/15
13 और 15 का LCM 195 है।
दी गई प्रत्येक परिमेय संख्या को उपरोक्त LCM के समान हर के साथ व्यक्त करें।
अब,
(-6/13)= [(-6 × 15)/ (13 × 15)] = (-90/195)
(7/15)= [(7 × 13)/ (15 × 13)] = (91/195)
तब, = (-90/195) + (91/195) … [∵ दोनों परिमेय संख्याओं में हर समान है]
= (-90 + 91)/195
= (1/195)
(iv) 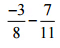
उत्तर: दी गई परिमेय संख्याओं के हरों का LCM लें।
8 और 11 का LCM 88 है।
दी गई प्रत्येक परिमेय संख्या को उपरोक्त LCM के समान हर के रूप में व्यक्त करें।
अब,
(-3/8)= [(-3 × 11)/ (8 × 11)] = (-33/88)
(7/11)= [(7 × 8)/ (11 × 8)] = (56/88)
तब, = (-33/88) – (56/88) … [∵ दोनों परिमेय संख्याओं में हर समान है]
= (-33 – 56)/88
= (-89/88)
(v) 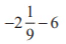 उत्तर: सबसे पहले हमें मिश्रित भिन्न को अनुचित भिन्न में बदलना होगा,
उत्तर: सबसे पहले हमें मिश्रित भिन्न को अनुचित भिन्न में बदलना होगा,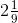 = -19/9हमारे पास है, -19/9 – 6दी गई परिमेय संख्याओं के हरों का LCM लें।
= -19/9हमारे पास है, -19/9 – 6दी गई परिमेय संख्याओं के हरों का LCM लें।
9 और 1 का LCM 9 है
दी गई प्रत्येक परिमेय संख्या को उपरोक्त LCM के सामान्य हर के रूप में व्यक्त करें।
अब,
(-19/9)= [(-19 × 1)/ (9 × 1)] = (-19/9)
(6/1)= [(6 × 9)/ (1 × 9)] = (54/9)
तब, = (-19/9) – (54/9) … [∵ दोनों परिमेय संख्याओं में हर समान है]
= (-19 – 54)/9
= (-73/9)
प्रश्न 3: गुणनफल ज्ञात कीजिए:
(i) (9/2) × (-7/4)
उत्तर: दो परिमेय संख्याओं का गुणनफल = (उनके अंश का गुणनफल) / (उनके हर का गुणनफल)
उपरोक्त प्रश्न को
(9/2) × (-7/4) के रूप में लिखा जा सकता है
। हमारे पास है,
= (9 × -7) / (2 × 4)
= -63/8
(ii) (3/10) × (-9)
उत्तर: दो परिमेय संख्याओं का गुणनफल = (उनके अंश का गुणनफल) / (उनके हर का गुणनफल)
उपरोक्त प्रश्न को
(3/10) × (-9/1) के रूप में लिखा जा सकता है
। हमारे पास है,
= (3 × -9) / (10 × 1)
= -27/10
(iii) (-6/5) × (9/11)
उत्तर: दो परिमेय संख्याओं का गुणनफल = (उनके अंश का गुणनफल) / (उनके हर का गुणनफल)
हमारे पास है,
= (-6 × 9) / (5 × 11)
= -54/55
(iv) (3/7) × (-2/5)
उत्तर: दो परिमेय संख्याओं का गुणनफल = (उनके अंश का गुणनफल) / (उनके हर का गुणनफल)
हमारे पास है,
= (3 × -2) / (7 × 5)
= -6/35
(v) (3/11) × (2/5)
उत्तर: दो परिमेय संख्याओं का गुणनफल = (उनके अंश का गुणनफल) / (उनके हर का गुणनफल)
हमारे पास है,
= (3 × 2) / (11 × 5)
= 6/55
(vi) (3/-5) × (-5/3)
उत्तर: दो परिमेय संख्याओं का गुणनफल = (उनके अंश का गुणनफल) / (उनके हर का गुणनफल)
हमारे पास है,
= (3 × -5) / (-5 × 3)
सरल करने पर, = (1 × -1) / (-1 × 1)
= -1/-1 = 1
प्रश्न 4: का मान ज्ञात कीजिए:
(i) (-4) ÷ (2/3)
उत्तर: हमारे पास है,
= (-4/1) × (3/2) … [∵ (2/3) का व्युत्क्रम (3/2) है]
दो परिमेय संख्याओं का गुणनफल = (उनके अंश का गुणनफल) / (उनके हर का गुणनफल)
= (-4 × 3) / (1 × 2) = (-2 × 3) / (1 × 1) = -6
(ii) (-3/5) ÷ 2
उत्तर: हमारे पास है,
= (-3/5) × (1/2) … [∵ (2/1) का व्युत्क्रम (1/2) है]
दो परिमेय संख्याओं का गुणनफल = (उनके अंश का गुणनफल) / (उनके हर का गुणनफल)
= (-3 × 1) / (5 × 2)
= -3/10
(iii) (-4/5) ÷ (-3)
उत्तर: हमारे पास है,
= (-4/5) × (1/-3) … [∵ (-3) का व्युत्क्रम (1/-3) है]
दो परिमेय संख्याओं का गुणनफल = (उनके अंश का गुणनफल) / (उनके हर का गुणनफल)
= (-4× (1)) / (5× (-3))
= -4/-15 = 4/15
(iv) (-1/8) ÷ 3/4
उत्तर: हमारे पास है,
= (-1/8) × (4/3) … [∵ (3/4) का व्युत्क्रम (4/3) है]
दो परिमेय संख्याओं का गुणनफल = (उनके अंश का गुणनफल) / (उनके हर का गुणनफल)
= (-1 × 4) / (8 × 3)
= (-1 × 1) / (2 × 3) = -1/6
(v) (-2/13) ÷ 1/7
उत्तर: हमारे पास है,
= (-2/13) × (7/1) … [∵ (1/7) का व्युत्क्रम (7/1) है]
दो परिमेय संख्याओं का गुणनफल = (उनके अंश का गुणनफल) / (उनके हर का गुणनफल)
= (-2 × 7) / (13 × 1)
= -14/13
(vi) (-7/12) ÷ (-2/13)
उत्तर: हमारे पास है, = (-7/12) × (13/-2) … [∵ (-2/13) का व्युत्क्रम (13/-2) है]
दो परिमेय संख्याओं का गुणनफल = (उनके अंश का गुणनफल) / (उनके हर का गुणनफल)
= (-7× 13) / (12× (-2))
= -91/-24 = 91/24
(vii) (3/13) ÷ (-4/65)
उत्तर: हमारे पास है, = (3/13) × (65/-4) … [∵ (-4/65) का व्युत्क्रम (65/-4) है]
दो परिमेय संख्याओं का गुणनफल = (उनके अंश का गुणनफल) / (उनके हर का गुणनफल)
= (3 × 65) / (13 × (-4))
= 195/-52 = -15/4
|
50 videos|152 docs|70 tests
|
FAQs on तर्कसंगत संख्याएँ NCERT Solutions - गणित और शिक्षाशास्त्र (Mathematics) CTET & TET Paper 2 - CTET & State TET
| 1. तर्कसंगत संख्याएँ क्या होती हैं? |  |
| 2. NCERT पाठ्यक्रम में तर्कसंगत संख्याओं का महत्व क्या है? |  |
| 3. CTET और State TET परीक्षा में तर्कसंगत संख्याओं से संबंधित प्रश्न कैसे आते हैं? |  |
| 4. तर्कसंगत संख्याओं को पहचानने के लिए क्या विधियाँ हैं? |  |
| 5. क्या तर्कसंगत संख्याएँ और अपरिमेय संख्याएँ एक ही श्रेणी में आती हैं? |  |
















