Encoding Schemes and Number System Chapter Notes | Computer Science for Class 11 - Humanities/Arts PDF Download
Introduction to Encoding Schemes and Number System
- When you press a key on your computer keyboard, like the letter “A,” the computer needs to understand it in its own language, which is binary code made up of 0s and 1s. This process is called encoding.
- Each key on the keyboard is mapped to a unique code before being converted into binary. For example, when you press “A,” it is mapped to the decimal value 65, which is then converted to binary for the computer to understand.
- Different keys, like the Hindi letter “अ,” are mapped to different codes. The letter “अ” is mapped to the hexadecimal value 0905, which translates to the binary code 0000100100000101.
- Encoding is like creating a secret code for data so that only the intended receiver can understand it. This process is also known as encryption. Standard encoding schemes ensure that each letter, number, and symbol is assigned a unique code, making it easier for computers to understand the input from keyboards.
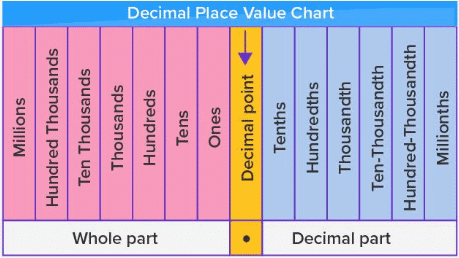
- A number system is a way of expressing numbers using a set of digits. For example, in the decimal number system, we use the digits 0 to 9, and each position in a number represents a power of 10.
- The binary number system, which is fundamental to computers, uses only two digits: 0 and 1. Each position in a binary number represents a power of 2.
- Other number systems, like octal (base 8) and hexadecimal (base 16), use different sets of digits and have their own rules for representing numbers. For instance, in the hexadecimal system, the digits go from 0 to 9 and then from A to F, where A represents 10, B represents 11, and so on, up to F, which represents 15.
- Understanding different number systems is crucial for various applications in computer science, including programming, data representation, and networking.
American Standard Code for Information Interchange (ASCII)
- In the 1960s, computers couldn't communicate because they represented keyboard keys differently. To solve this, a common standard called ASCII was developed to standardize character representation. ASCII is still widely used today.
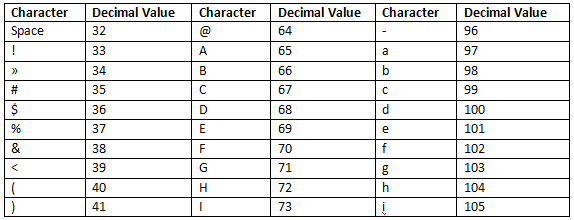
- Initially, ASCII used 7 bits to represent characters, allowing for 128 different combinations (27 = 128). This was sufficient for the English keyboard but limited to English characters.
- Over time, ASCII was expanded to include more characters, but the original 7-bit system only covered English letters, digits, and some special characters.
Printable Characters in ASCII
Example: Encoding the word "DATA" in ASCII
- D: ASCII value is 68, binary code is 1000100
- A: ASCII value is 65, binary code is 1000001
- T: ASCII value is 84, binary code is 1010100
ASCII and Binary values for the word "DATA"

Indian Script Code for Information Interchange (ISCII)
To promote the use of Indian languages on computers, a standardized coding system for Indian scripts known as ISCII was created in India during the mid-1980s. This 8-bit code can represent 256 characters, retaining all 128 ASCII codes and using the remaining codes for additional Indian language characters. The extra codes, assigned in the range of 160 to 255, are used for the 'aksharas' of various Indian languages.
UNICODE
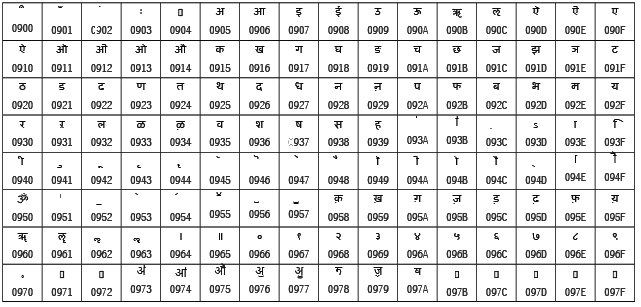
Various encoding schemes existed for different language character sets, but they were incompatible, leading to recognition issues across different systems. To address this, UNICODE was established as a standard to encompass all characters from every written language worldwide. UNICODE assigns a unique number to each character, regardless of the device, operating system, or software application used. Common UNICODE encodings include UTF-8, UTF-16, and UTF-32. UNICODE is a superset of ASCII, with values 0 to 128 corresponding to the same characters as in ASCII. For instance, the Devanagari script in UNICODE is presented in a table format, showing characters alongside their hexadecimal values.
Unicode table for the Devanagari script
Number System
Number System is a method to represent numbers. Number system is also called positional number system because the value of each symbol (i.e., digit and alphabet) in a number depends upon its position within the number.
Number systems are also called positional number system because the value of each symbol (i.e., digit and alphabet) in a number depends upon its position within the number. Number may also have a fractional part similar to decimal numbers used by us.
The symbol at the right most position in the integer part in a given number has position 0. The value of position (also called position value) in the integer part increases from right to left by 1. On the other hand, the first symbol in the fraction part of the number has position number –1, which decreases by 1 while reading fraction part from left to right.
Each symbol in a number has a positional value, which is computed using its position value and the base value of the number system.
The symbol at position number 3 in a decimal system with base 10 has positional value 103. Adding the product of positional value and the symbol value results in the given number.
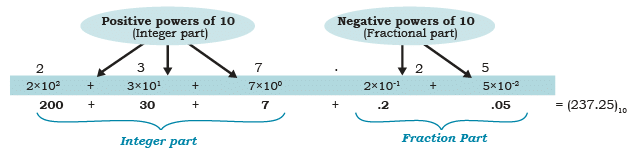
For Example: (123.45) 10 = 1 × 102 + 2 × 101 + 3 × 100 + 4 × 10−1 + 5 × 10−2
Decimal Number System
The decimal number system, commonly used in everyday life, is also known as the base-10 system because it employs 10 digits, ranging from 0 to 9. In this system, a number is represented by two components: the symbol value (a digit from 0 to 9) and the positional value, which is determined by its position in relation to the base value.
Positional value for digits of decimal number represented as power of base 10
Binary Number System
The base value in a number system helps differentiate a number in one system from a number in another. It is written as a subscript next to the number. For instance, (70) 8 indicates 70 as an octal number, while (70) 10 signifies 70 as a decimal number.
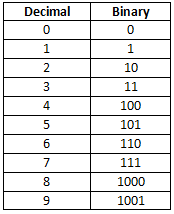
In computers, Integrated Circuits (ICs) are composed of numerous transistors activated by electronic signals, which can be low or high. The ON (high) and OFF (low) states of a transistor are represented by the digits 1 and 0, respectively. This forms the basis of the binary number system, also known as the base-2 system, which consists of only two digits: 1 and 0. Examples of binary numbers include 1001011, 1011.101, and 111111.01. Binary numbers can be converted to their equivalent decimal numbers for easier understanding by humans.
Table 2.4 Binary value for (0–9) digits of decimal number system
Octal Number System
The octal number system, also known as the base-8 system, was developed for the compact representation of binary numbers. In this system, there are eight digits (0-7), and the positional value is expressed in powers of 8. Since three binary digits (23 = 8) are sufficient to represent any octal digit, the octal system provides a more manageable way to express large binary numbers.
Octal Digits and Their Binary Representation
- The table below shows the decimal and binary equivalents of the eight octal digits:
Examples of Octal Numbers
- (237.05)8
- (13) 8
- (617.24)8
Hexadecimal Number System
The hexadecimal number system, also known as the base-16 system, is used for the compact representation of binary numbers. It consists of 16 unique symbols: 0-9 and A-F, where A, B, C, D, E, and F represent the decimal numbers 10 through 15. In the hexadecimal system, each alphanumeric digit is represented by a group of 4 binary digits because 4 bits (24 = 16) are sufficient to represent the 16 alphanumeric symbols.
Hexadecimal Symbols and Their Binary Representation
- The table below shows the decimal and binary equivalents of the hexadecimal symbols:
Examples of Hexadecimal Numbers
- (23A.05)16
- (1C3)16
- (619B.A)16
Applications of Hexadecimal Number System
Memory Addressing:
- Simplifying Address Representation: Main memory consists of numerous memory locations, each identified by a unique address. These addresses are typically 16-bit or 32-bit in size. Handling a 16-bit memory address in binary, such as 1100000011110001, can be cumbersome for programmers. To make this representation easier, hexadecimal (and octal) notation is used. For instance, the binary address 1100000011110001 is more conveniently expressed in hexadecimal as C0F1. This simplification aids programmers in managing memory addresses more efficiently.
- Example of Address Conversion: Consider the 16-bit binary address 1100000011110001. In hexadecimal, this address is represented as C0F1, and in octal, it is 140361. This conversion highlights how hexadecimal and octal representations make it easier to work with complex binary addresses.
Web Color Representation:
- RGB Color Model: Hexadecimal numbers play a crucial role in defining colors on the web. Colors are created using three primary components: Red, Green, and Blue, commonly referred to as the RGB model. Each color in this model is typically chosen from a palette of 16 million possible colors, requiring 24 bits for representation (8 bits for each of the three components).
- Compact Representation of Color Codes: Remembering a 24-bit binary color code can be challenging. To simplify this, color codes are often written in hexadecimal form. For example, the binary code for the color RED, which is 11111111,00000000,00000000 in binary, is represented in hexadecimal as FF,00,00. This compact representation makes it easier to remember and use color codes.
Examples of Color Codes:
- Black: (0,0,0) in decimal, (00000000,00000000,00000000) in binary, and (00,00,00) in hexadecimal.
- White: (255,255,255) in decimal, (11111111,11111111,11111111) in binary, and (FF,FF,FF) in hexadecimal.
- Yellow: (255,255,0) in decimal, (11111111,11111111,00000000) in binary, and (FF,FF,00) in hexadecimal.
- Grey: (128,128,128) in decimal, (10000000,10000000,10000000) in binary, and (80, 80, 80) in hexadecimal.
Conversion Between Number Systems
In the previous section, we explored various number systems utilized in computers. Now, let's delve into how to convert a number from one system to another, enhancing our understanding of how numbers are represented in computers. While humans commonly use the decimal number system, digital systems operate on binary numbers. Octal and hexadecimal systems serve to simplify binary representation for easier comprehension.
Conversion from Decimal to Other Number Systems
When converting a decimal number to another system, such as binary, octal, or hexadecimal, follow these steps:
- Step 1: Divide the number by the base value of the target number system.
- Step 2: Note the remainder.
- Step 3: Continue dividing the quotient by the base value, noting the remainders, until the quotient becomes zero.
- Step 4: Write the remainders in reverse order (from bottom to top).
(A) Decimal to Binary Conversion
To convert a decimal number to binary, follow these steps:
- Step 1: Divide the decimal number by 2 (the base value of the binary system).
- Step 2: Record the remainder.
- Step 3: Continue dividing the quotient by 2 and noting the remainders until the quotient is zero.
- Step 4: Collect the remainders from bottom to top to obtain the binary equivalent.
For example, let's convert (65)10 to binary:
- 65 ÷ 2 = 32, Remainder: 1
- 32 ÷ 2 = 16, Remainder: 0
- 16 ÷ 2 = 8, Remainder: 0
- 8 ÷ 2 = 4, Remainder: 0
- 4 ÷ 2 = 2, Remainder: 0
- 2 ÷ 2 = 1, Remainder: 0
- 1 ÷ 2 = 0, Remainder: 1
Collecting the remainders from bottom to top, we get (1000001)2, which confirms that (65)10 = (1000001)2.
(B) Decimal to Octal Conversion
Process:
Step 1: Divide the decimal number by 8.
Step 2: Note the remainder.
Step 3: Continue dividing the quotient by 8, noting the remainder, until the quotient is zero.
Step 4: Read the remainders from bottom to top to get the octal equivalent.
Example: Convert (122)10 to octal number.
Sol: 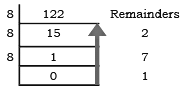 Therefore, (122)10 = (172)8
Therefore, (122)10 = (172)8
(C) Decimal to Hexadecimal Conversion
Process:
Step 1: Divide the decimal number by 16.
Step 2: Note the remainder.
Step 3: Continue dividing the quotient by 16, noting the remainder, until the quotient is zero.
Step 4: Read the remainders from bottom to top to get the hexadecimal equivalent.
Example: Convert (122)10 to hexadecimal.
Sol: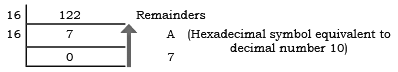 Therefore, (122)10 = (7A)16
Therefore, (122)10 = (7A)16
Conversion of Other Number Systems to Decimal Number System
To convert a number from bases 2, 8, or 16 to its decimal equivalent, follow these steps:
Step 1: Assign Position Numbers
Write down the position number for each alphanumeric symbol in the given number, starting from 0 on the right.
Step 2: Calculate Positional Values
Calculate the positional value for each symbol by raising the base value (2, 8, or 16) to the power of its position number.
Step 3: Multiply and Convert
Multiply each digit by its corresponding positional value to get the decimal equivalent for that digit.
Step 4: Sum the Values
Add all the decimal values together to obtain the equivalent decimal number.
(A) Binary Number to Decimal Number
Since binary number system has base 2, the positional values are computed in terms of powers of 2. Using the above mentioned steps we can convert
Example: Convert (1101)2 into decimal number.
Sol: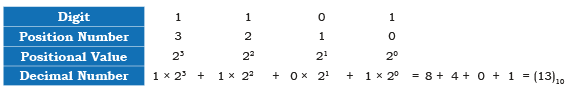 Note: Add the product of positional value and corresponding digit to get decimal number.
Note: Add the product of positional value and corresponding digit to get decimal number.
(B) Octal to Decimal Conversion
To convert an octal number to decimal, use the base value 8, which is equivalent to 23. This is why 3 bits in a binary number are grouped together to form an octal number.
Example: Convert (257)8 to decimal:
Sol: 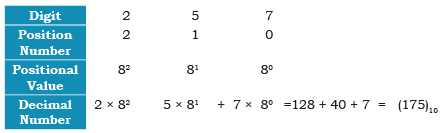
(C) Hexadecimal Number to Decimal Number
To convert a hexadecimal number into a decimal number, follow the steps outlined in this section, using the base value of 16 from the hexadecimal number system. When performing the calculation, use the decimal value equivalent of the alphabet symbols in the hexadecimal number.
Example: Convert (3A5)16 into a decimal number.
Sol:
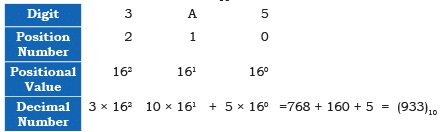
Conversion from Binary Number to Octal/ Hexadecimal Number and Vice-Versa
A binary number can be converted to octal or hexadecimal by grouping bits and replacing each group with its equivalent octal or hexadecimal digit.
(A) Binary Number to Octal Number
To convert a binary number to an octal number, group the binary digits into sets of 3 bits from right to left. Replace each 3-bit group with the corresponding octal digit. If the number of bits in the binary number is not a multiple of 3, add the necessary number of zeros to the most significant position of the binary number.
Example 2.9: Convert (10101100)2 to an octal number.
Sol: Group the given binary number into 3-bit groups from right to left:
(10)(101)(100)
Write the octal equivalent for each 3-bit group:
(2)(5)(4)
Therefore, (10101100)2 = (254)8
(B) Octal Number to Binary Number
To convert an octal number to a binary number, replace each octal digit with its corresponding 3-digit binary number.
Example: Convert (705)8 to a binary number.
Sol: Replace each octal digit with its 3-bit binary value:  Therefore, (705)8 = (111000101)2
Therefore, (705)8 = (111000101)2
(C) Converting Binary Numbers to Hexadecimal Numbers
- To convert a binary number to its equivalent hexadecimal number, follow these steps:
- Grouping: Make groups of 4 binary digits (bits) from right to left. If necessary, add leading zeros to the most significant position of the binary number to ensure the total number of bits is a multiple of 4.
- Substitution: Replace each 4-bit group with its corresponding hexadecimal symbol.
Example: Convert (0110101100)2 to hexadecimal.
- Group the binary number into 4-bit segments from right to left: 0001 1010 1100
- Substitute each group with its hexadecimal equivalent: (1AC)16
Why Group 4 Bits for Hexadecimal Conversion?
- The base of the hexadecimal number system is 16, which can be expressed as 16 = 24. This means that 4 binary digits are sufficient to represent all 16 hexadecimal symbols.
(D) Converting Hexadecimal Numbers to Binary Numbers
To convert a hexadecimal number to its binary equivalent, replace each hexadecimal digit with its 4-bit binary equivalent and combine the results.
For example, to convert (23D)16 to binary:
Therefore, (23D)16 = (001000111101)2
Conversion of a Number with Fractional Part
(A) Decimal Number with Fractional Part to another Number System
- To convert the fractional part of a decimal number to another number system with base value b, repeatedly multiply the fractional part by the base value b till the fractional part becomes 0.
- Use integer part from top to bottom to get equivalent number in that number system.
- If the fractional part does not become 0 in successive multiplication, then stop after, say 10 multiplications.
- In some cases, fractional part may start repeating, then stop further calculation.
Example: Convert (0.25)10 to binary.
Sol:
Step 1: Multiply the fractional part (0.25) by 2:
- 0.25 × 2 = 0.50 (integer part: 0)
Step 2: Multiply the new fractional part (0.50) by 2:
- 0.50 × 2 = 1.00 (integer part: 1)
Step 3: Since the fractional part is now 0, we stop here.
Step 4: Write the integer parts from top to bottom to get the binary representation:
- (0.25) 10 = (0.01)2
Example: Convert (0.675) 10 to binary.
Sol:
- 0.675 × 2 = 1.350 (integer part: 1)
- 0.350 × 2 = 0.700 (integer part: 0)
- 0.700 × 2 = 1.400 (integer part: 1)
- 0.400 × 2 = 0.800 (integer part: 0)
- 0.800 × 2 = 1.600 (integer part: 1)
- 0.600 × 2 = 1.200 (integer part: 1)
- 0.200 × 2 = 0.400 (integer part: 0)
Step 3: Since the fractional part (0.400) is repeating, we stop here.
Step 4: Write the integer parts from top to bottom to get the binary number for the fractional part:
- (0.675)10 = (0.1010110)2
Example: Convert (0.675) 10 to octal.
Sol:
- 0.675 × 8 = 5.400 (integer part: 5)
- 0.400 × 8 = 3.200 (integer part: 3)
- 0.200 × 8 = 1.600 (integer part: 1)
- 0.600 × 8 = 4.800 (integer part: 4)
- 0.800 × 8 = 6.400 (integer part: 6)
Step 3: Since the fractional part (0.400) is repeating, we stop here.
Step 4: Write the integer parts from top to bottom to get the octal number for the fractional part:
- (0.675)10 = (0.53146)8
Example: Convert (0.675) 10 to hexadecimal form.
Sol:
- 0.675 × 16 = 10.800 (integer part: 10, A in hexadecimal)
- 0.800 × 16 = 12.800 (integer part: 12, C in hexadecimal)
Step 3: Since the fractional part (0.800) is repeating, we stop here.
Step 4: Write the integer parts from top to bottom to get the hexadecimal equivalent for the fractional part:
- (0.675)10 = (0. AC)16
(B) Non-decimal Number with Fractional Part to Decimal Number System
To convert a non-decimal number with a fractional part into the decimal number system, follow these steps:
1. Calculate the positional value of each digit based on its position and the base value.
2. Multiply the positional value by the digit and sum these products to obtain the equivalent decimal number with a fractional part.
Example: Convert (100101.101)2 into decimal.
Sol:
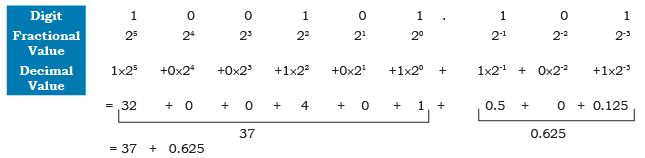
Therefore, (100101.101)2 = (37.625)10
Example: Convert (605.12)8 into decimal number.
Sol: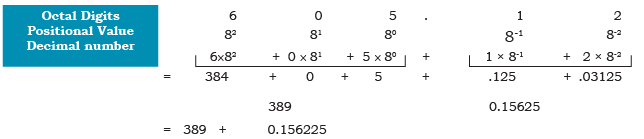
Therefore, (605.12)8 = (389.15625)10
(C) Fractional Binary Number to Octal or Hexadecimal Number
To convert a fractional binary number into octal or hexadecimal, follow these steps:
1. For the integer part, group the binary digits into 3-bit (for octal) or 4-bit (for hexadecimal) groups from right to left.
2. For the fractional part, group the binary digits into 3-bit (for octal) or 4-bit (for hexadecimal) groups from left to right.
3. Replace each group with its corresponding octal or hexadecimal digit.
4. If necessary, add 0s to the end of the fractional part to complete the last group.
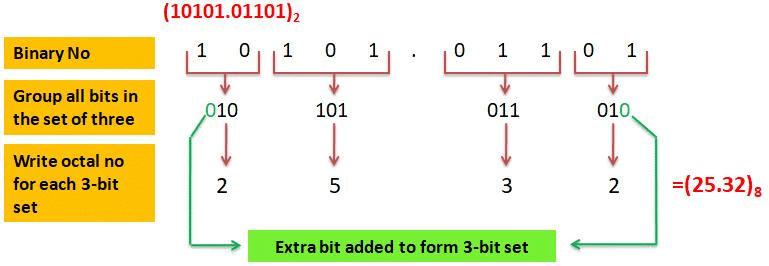
Example: Convert (10101100.01011)2 to octal number.
Sol: 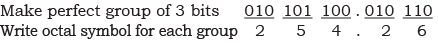
Therefore, (10101100.01011)2 = (254.26)8
Note: Make 3-bit groups from right to left for the integer part and left to right for the fractional part.
|
33 docs|11 tests
|
FAQs on Encoding Schemes and Number System Chapter Notes - Computer Science for Class 11 - Humanities/Arts
| 1. What are encoding schemes and why are they important in computer systems? |  |
| 2. What is the difference between the binary number system and the decimal number system? |  |
| 3. How do you convert a binary number to a decimal number? |  |
| 4. What are some common encoding schemes used for text data? |  |
| 5. Why is it important to understand different number systems in computer science? |  |
















