Introduction to Problem Solving Chapter Notes | Computer Science for Class 11 - Humanities/Arts PDF Download
| Table of contents |

|
| Introduction |

|
| Steps for Problem Solving |

|
| Algorithm |

|
| Representation of Algorithms |

|
| Flow of Control |

|
| Verifying Algorithms |

|
| Comparison of Algorithms |

|
| Coding |

|
| Decomposition |

|
Introduction
Computers are now an integral part of our daily lives, helping us perform tasks more quickly and accurately. For instance, booking train tickets online is made possible through the use of computers and smartphones.
India has a vast and complex railway network, making railway reservations a challenging task. This process involves managing a wide range of information, including details about different trains (such as train types, berth and compartment options, schedules), as well as handling multiple users trying to book tickets simultaneously.
Thanks to computers, booking train tickets has become much easier and more convenient. Online reservations allow us to secure tickets from anywhere at any time, enhancing our comfort and flexibility.
The term “computerisation” refers to the use of computers to develop software that automates routine human tasks efficiently. Problem-solving is a crucial skill in computer science because computers are used to tackle various everyday challenges. However, it’s important to note that computers cannot solve problems on their own. They require precise, step-by-step instructions from us. The effectiveness of a computer in solving a problem depends on how accurately and clearly we define the problem, design a solution (algorithm), and implement that solution (program) using a programming language.
In essence, problem-solving involves identifying an issue, creating an algorithm to address it, and then turning that algorithm into a computer program.
Steps for Problem Solving

When a vehicle makes a strange noise while driving, the first step is to identify the source of the noise. If the problem is beyond our ability to fix, we take the vehicle to a mechanic. The mechanic will analyze the issue, plan the necessary repairs, and fix the vehicle to eliminate the noise. This example illustrates that finding a solution to a problem often involves multiple steps.
Some problems are straightforward and easy to solve, while others are complex and require a systematic approach. Problem solving begins with clearly identifying the problem and ends with a working solution, such as a program or software. The key steps for solving a problem using a computer are shown in a figure and will be discussed in the following subsections.
Analyzing the Problem
Algorithm:
- A set of precise steps that, when followed, solve the problem or accomplish the desired task.
Before attempting to find a solution, it is crucial to fully understand the problem. If we are unclear about what needs to be solved, we may end up creating a program that does not meet our objectives. Therefore, it is essential to read and analyze the problem statement carefully to identify the main components and determine the core functionalities that our solution should have. By analyzing the problem, we can figure out the necessary inputs for our program and the expected outputs.
Algorithm Development
- Formulating a clear solution before diving into coding is crucial. An algorithm, written in natural language, serves as this solution. Think of it as a detailed recipe with specific steps to follow.
Coding
- After finalizing the algorithm, the next step is to translate it into a format that computers can understand. This involves using high-level programming languages.
- It's also important to document the coding process and the solution details. This documentation is useful for future reference when revisiting the programs.
Testing and Debugging
- The created program needs to be tested against various parameters to ensure it meets user requirements, responds within expected timeframes, and produces correct outputs for all possible inputs.
- Syntactical errors will prevent any output, while logical errors will lead to incorrect outputs. Standard testing methods like unit testing, integration testing, system testing, and acceptance testing are used in the software industry to ensure the software meets all business and technical requirements.
- Any errors found during testing are debugged and rectified, and the program is retested. This process continues until all errors are eliminated.
- Even after the software application is developed, tested, and delivered, issues may arise that need to be resolved over time. Maintenance involves fixing problems faced by the user and ensuring the software functions as expected.
Algorithm
- In our daily lives, we engage in various activities that require us to follow a specific order of steps.
- Examples of these activities include:
- Getting ready for school
- Making breakfast
- Riding a bicycle
- Wearing a tie
- Solving a puzzle
- To successfully complete each of these activities, we need to adhere to a sequence of actions.
Let us now find Greatest Common Divisor (GCD) of two numbers 45 and 54.
Note: GCD is the largest number that divides both the given numbers.
Step 1: Find the numbers (divisors) which can divide the given numbers
Divisors of 45 are: 1, 3, 5, 9, 15, and 45 Divisors of 54 are: 1, 2, 3, 6, 9, 18, 27, and 54
Step 2: Then find the largest common number from these two lists.
Therefore, GCD of 45 and 54 is 9
Hence, it is clear that we need to follow a sequence of steps to accomplish the task. Such a finite sequence of steps required to get the desired output is called an algorithm. It will lead to the desired result in a finite amount of time, if followed correctly. Algorithm has a definite beginning and a definite end, and consists of a finite number of steps.
Why Do We Need an Algorithm?
- A programmer creates a program to guide the computer in performing specific tasks. The computer follows the instructions written in the program code. Before writing the code, the programmer prepares a roadmap of the program, outlining the steps to be taken. This roadmap is essential because it helps the programmer visualize the instructions clearly. Without it, the programmer might end up creating a program that doesn't work as intended.
- An algorithm isthis roadmap,and it is the fundamental building block of a computer program.
- Many everyday activities, such as searching online, sending messages, finding words in documents, booking taxis through apps, online banking, and playing computer games, are all based on algorithms.
- Writing an algorithm is considered the first step in programming. Once an algorithm is in place to solve a problem, the programmer can write the computer program in a high-level language. If the algorithm is correct, the computer will execute the program accurately every time.
- The purpose of using an algorithm is to enhance the reliability, accuracy, and efficiency of finding solutions.
(A) Characteristics of a Good Algorithm
- Precision: The steps in the algorithm are stated or defined with precision, leaving no room for ambiguity.
- Uniqueness: The outcome of each step is uniquely determined and depends only on the input and the result of the previous steps.
- Finiteness: The algorithm is designed to stop after a finite number of steps, ensuring that it does not run indefinitely.
- Input: The algorithm accepts some input to work with.
- Output: The algorithm produces some output as a result of its processing.
(B) While writing an algorithm, it is required to clearly identify the following:
- The input to be taken from the user
- Processing or computation to be performed to get the desired result
- The output desired by the user
Representation of Algorithms
Using their algorithmic thinking skills, software designers or programmers analyse the problem and identify the logical steps necessary to reach a solution. Once these steps are identified, it is essential to write them down along with the required input and desired output. There are two common methods for representing an algorithm: flowchart and pseudocode. Either method can be used to represent an algorithm, keeping in mind the following considerations:
- It should showcase the logic of the problem solution, excluding any implementational details.
- It should clearly reveal the flow of control during the execution of the program.
Flowchart — Visual Representation of Algorithms
A flowchart is a visual representation of an algorithm, consisting of a diagram made up of boxes, diamonds, and other shapes connected by arrows. Each shape represents a step in the solution process, and the arrows indicate the order or link among the steps.
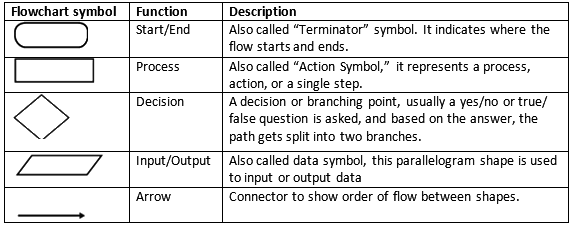
There are standardized symbols for drawing flowcharts.
Shapes or Symbols to Draw Flowcharts
Example : Write an algorithm to find the square of a number.
Before developing the algorithm, let us first identify the input, process, and output:
- Input: Number whose square is required
- Process: Multiply the number by itself to get its square
- Output: Square of the number
Algorithm to find the square of a number:
Step 1: Input a number and store it in num
Step 2: Compute num * num and store the result in square
Step 3: Print square
The algorithm to find the square of a number can be represented pictorially using a flowchart.
Flowchart to calculate square of a number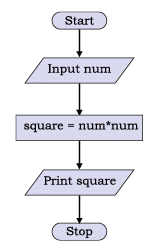
Flowchart to solve the problem of a non-functioning light bulb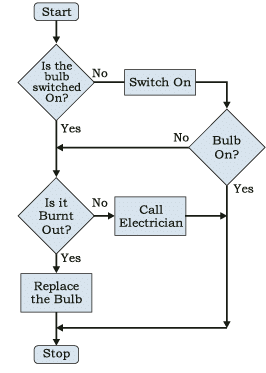
Pseudocode
- A pseudocode (pronounced Soo-doh-kohd) is a different way to show an algorithm.
- It is a kind of informal language that helps programmers write algorithms.
- Pseudocode offers a clear explanation of the steps a computer must take, arranged in a specific order.
- It is designed for human readers and cannot be run directly by a computer.
- There is no set rule for how to write pseudocode.
- The term pseudo means not real, so pseudocode means not actual code.
- Some common keywords used in pseudocode include:
- INPUT
- COMPUTE
- INCREMENT
- DECREMENT
- IF/ELSE
- WHILE
- TRUE/FALSE
Example: Write an algorithm to display the sum of two numbers entered by user, using both pseudocode and flowchart.
Sol: Pseudocode for the sum of two numbers will be:
INPUT num1
INPUT num2
COMPUTE Result = num1 + num2
PRINT Result
The flowchart for this algorithms is given in Figure.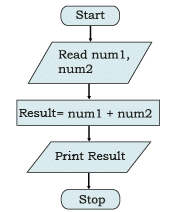
Example: Write an algorithm to calculate area and perimeter of a rectangle, using both pseudocode and flowchart.
Sol:
Pseudocode for calculating area and perimeter of a rectangle.
INPUT length
INPUT breadth
COMPUTE Area = length * breadth
PRINT Area
COMPUTE Perim = 2 * (length + breadth)
PRINT Perim
The flowchart for this algorithm is given in Figure.
(A) Benefits of Pseudocode
Pseudocode offers several advantages when it comes to planning and understanding programs:
- Clarity of Functionality: Pseudocode helps in outlining the basic functionality of a program before diving into actual coding. It acts as a blueprint, ensuring that no important step is overlooked.
- Readability for Non-Programmers: For individuals who may not be familiar with programming languages, pseudocode provides a more accessible way to grasp the steps involved in a program. It allows them to review the logic and confirm that the proposed implementation will yield the desired output.
- Error Prevention: By writing in a human-readable format first, programmers can catch potential errors or omissions early in the process. This reduces the risk of bugs in the final code.
- Focus on Logic: Pseudocode encourages programmers to focus on the logic and sequence of steps without getting bogged down by the syntax of a specific programming language.
Flow of Control
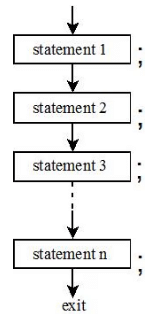
The flow of control refers to the order in which events or actions are executed in a program or algorithm. It can follow a specific sequence, branch based on decisions, or repeat certain actions a finite number of times. Understanding the flow of control is essential for designing effective algorithms that can handle different scenarios.
Here are the three main types of flow of control:
1. Sequence:
In a sequence flow, statements are executed one after the other in a linear order. This is the simplest form of flow where all steps are carried out one after the other without any deviation. For example, in a recipe, the instructions are followed in the order they are given, such as mixing ingredients, then baking, and finally cooling.
2. Selection:
Selection flow involves making decisions based on certain conditions. Depending on the outcome of a condition, different paths can be taken. For instance, in a navigation app, the route from home to school may vary based on traffic conditions. In the morning, the shortest route might be selected, but in the afternoon, a different route with less traffic may be chosen. This type of flow is also seen in situations like checking eligibility for voting based on age.
When traveling between home and school, there can be multiple routes available. In the morning, we might take the shortest route. However, in the afternoon, the same route could have heavy traffic, so we might choose a different one with less congestion. This situation requires making a decision based on certain conditions.
Let's explore more examples where decision-making depends on conditions:
Checking Voting Eligibility
A person's ability to vote depends on their age:- If the person is 18 years or older, they are eligible to vote.
- If the person is younger than 18, they are not eligible to vote.
Grouping Students Based on Age and Interest
Suppose we have the following rule:- If a student is 8 years old and likes Maths, they are placed in Group A.
- Otherwise, they go to Group B.
- Based on this condition:
- Ravi (8 years old, dislikes Maths): Group B
- Priti (8 years old, likes Maths): Group A
- Anish (7 years old, likes Maths): Group B
These examples show how conditions help in decision-making by choosing one of the possible outcomes. In programming, such decisions are made using conditional statements, which check conditions and perform actions based on whether they are true or false (binary values).
Writing Conditions in Algorithms
If <condition> then
steps to be taken when the condition is true/fulfilled
There are situations where we also need to take action when the condition is not fulfilled. To represent that, we can write: 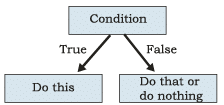 If <condition> is true then steps to be taken when the condition is true/fulfilled otherwise
If <condition> is true then steps to be taken when the condition is true/fulfilled otherwise
steps to be taken when the condition is false/not fulfilled
In programming languages, the 'otherwise' condition is represented using the else keyword. Therefore, a true/false conditional is implemented using an if-else block in actual programs.
Example 1: Checking Whether a Number is Odd or Even
Algorithm:
- Input: A number
- Process: Check if the number is even or odd
- Output: Print “Even” or “Odd”
Pseudocode:
PRINT "Enter the Number
INPUT numbe
IF number MOD 2 == 0 THEN
PRINT "Number is Even"
ELSE
PRINT "Number is Odd"
Example 2: Categorizing a Person Based on Age
A person is classified as a child, teenager, or adult based on their age.
- Input: Age
- Process: Check age against given conditions
- Output: Print either “Child,” “Teenager,” or “Adult”
Pseudocode:
INPUT Age
IF Age < 13 THEN
PRINT "Child"
ELSE IF Age < 20 THEN
PRINT "Teenager"
ELSE
PRINT "Adult"
Repetition
Repetition, also known as iteration or looping, is a fundamental concept in programming. It involves executing a set of instructions repeatedly until a specified condition is met. This is similar to how we give directions or instructions in everyday life, where we ask someone to do something a certain number of times or until a certain point is reached.
For example, when we say, "Clap your hands five times," we are asking for a specific action to be repeated a certain number of times. In programming, we use loops to automate such repetitive tasks.
Consider the card game example where we need to withdraw 10 cards to decide the winner. The same set of instructions needs to be repeated 10 times to complete the task.
Similarly, in our daily routines, there are various activities that involve repetition, such as brushing our teeth, getting dressed, or having meals. These activities follow a specific sequence of steps that are repeated every day.
Example: Finding the Average of 5 Numbers
Pseudocode:
- Step 1: Initialize count and sum to 0
- Step 2: Repeat Steps 3 to 5 while count is less than 5
- Step 3: Input a number and add it to sum
- Step 4: Increment count by 1
- Step 5: Compute average by dividing sum by 5
- Step 6: Print average
Explanation:
In this example, a counter named "count" keeps track of how many times the loop has run. After each iteration, the count is increased by 1 until it reaches the specified limit.
There are situations where we do not know in advance how many times a set of instructions needs to be repeated. In such cases, we use a "WHILE" construct to handle unknown repetitions.
Example: Accepting Numbers Until 0 is Entered
Pseudocode:
- Step 1: Initialize sum and count to 0
- Step 2: Input a number num
- Step 3: While num is not equal to 0, repeat Steps 4 to 6
- Step 4: Add num to sum
- Step 5: Increment count by 1
- Step 6: Input a new number num
- Step 7: Compute average by dividing sum by count
- Step 8: Print average
Explanation:
In this example, we divide the sum by count to calculate the average because count represents the total number of valid inputs.
The input statement for num is used twice to allow the user to enter a new number during each iteration of the loop.
In this instance, we are unsure about the number of inputs a user will provide before entering 0. This uncertainty is managed by continuously checking the condition until it becomes false.
Verifying Algorithms
Importance of Verification:
- Verifying algorithms is crucial to ensure they function correctly and produce the desired results.
- Faulty algorithms can lead to significant issues, especially in critical applications like banking, healthcare, and aerospace.
Example of Verification: Sum of First N Natural Numbers
- To verify the formula for the sum of the first N natural numbers, we can check it for small values of N.
- For instance, when N = 6, the sum is 1 + 2 + 3 + 4 + 5 + 6 = 21.
- Using the formula N(N+1)/2, we calculate 6(6+1)/2 = 21, confirming the formula's correctness.
Dry Run Method:
- The dry run method involves taking different input values and manually going through all the steps of the algorithm to ensure it produces the expected output.
- This method helps identify incorrect steps, missing details, and specifics in the algorithm.
Importance of Input Selection:
- Choosing the right input values for testing is crucial.
- If all possible input values are not tested, the program may fail in certain cases.
Activity 4.5: Algorithm for Area and Perimeter of a Rectangle
- Write an algorithm to calculate the area and perimeter of a rectangular shape given the length and breadth in feet and inches (e.g., 5 ft 6 inch).
Notes
Concept of Algorithm:
Definition: A step-by-step set of instructions to solve a problem is called an algorithm.
Example: Addition of time
- We want to add two times, say T1 and T2, where T1 = 5 hours 20 minutes and T2 = 7 hours 30 minutes.
- We will create an algorithm to add these two times together.
Step 1: Input the values
- PRINT value for T1
- INPUT hh1 (hours of T1)
- INPUT mm1 (minutes of T1)
Step 2: Input the values for T2
- PRINT value for T2
- INPUT hh2 (hours of T2)
- INPUT mm2 (minutes of T2)
Step 3: Calculate the total time
- hh_total = hh1 + hh2 (Add hours)
- mm_total = mm1 + mm2 (Add minutes)
Step 4: Adjust if necessary
- IF mm_total >= 60 THEN
- hh_total = hh_total + 1 (Add an hour)
- mm_total = mm_total - 60 (Subtract 60 minutes)
Step 5: Output the total time
- PRINT T_total as hh_total, mm_total
Verification:
- Example 1: T1 = 5 hrs 20 mins and T2 = 7 hrs 30 mins
- Calculation: hh_total = 5 + 7 = 12, mm_total = 20 + 30 = 50
- Result: T_total = 12 hrs 50 mins (Correct)
Example 2: T1 = 4 hrs 50 mins and T2 = 2 hrs 20 mins
- Calculation: hh_total = 4 + 2 = 6, mm_total = 50 + 20 = 70
- Result: T_total = 6 hrs 70 mins (Incorrect)
Correction:
- Since mm_total >= 60, we need to adjust
- hh_total = 6 + 1 = 7, mm_total = 70 - 60 = 10
- Correct Result: T_total = 7 hrs 10 mins
Importance of Verification:
- Verifying algorithms is crucial because if there are errors in the algorithm, the software developed based on it will not work correctly.
- Catching and fixing mistakes in the algorithm early is much easier than trying to correct them later in the software.
Comparison of Algorithms
There can be multiple approaches to solve a problem using a computer, leading to the creation of different algorithms. This raises the question of which algorithm should be used.
Let's consider the problem of determining whether a given number is prime or not. Prime numbers are crucial in computer science and have applications in areas such as databases, security, file compression and decompression, modulation, and demodulation. There are four different algorithms to check if a number is prime:
(i) Starting with divisor 2, divide the given number (dividend) and check for factors. Increase the divisor in each iteration and repeat the process until the divisor is less than the dividend. If a factor is found, the number is not prime.
(ii) In this method, instead of testing all numbers up to the dividend, only test up to half of the dividend, as the divisor cannot be more than half of the dividend.
(iii) In this method, test divisibility only up to the square root of the dividend.
(iv) Given a list of prime numbers up to 100, divide the given number by each prime in the list. If the number is not divisible by any of these primes, it is prime; otherwise, it is not.
All four methods can determine if a number is prime, but the question is which method is more efficient.
Algorithm (i) requires a large number of calculations and more processing time, especially for large numbers. It checks all numbers until the divisor is less than the number, making it time-consuming for large inputs.
Algorithm (ii) improves efficiency by checking for divisibility only up to half of the number, reducing computation time compared to (i).
Algorithm (iii) is even more efficient as it checks for divisibility only up to the square root of the number, further reducing computation time.
Algorithm (iv) uses only prime numbers smaller than the given number for divisibility, reducing calculations. However, it requires additional memory to store the list of prime numbers.
Time Complexity
- Time complexity refers to the amount of time an algorithm takes to complete as a function of the length of the input.
- It helps in estimating the time required for an algorithm to run and is usually expressed using Big O notation.
- For example, an algorithm with a time complexity of O(n) will take time proportional to the size of the input.
Space Complexity
- Space complexity refers to the amount of memory space required by an algorithm to complete as a function of the length of the input.
- It includes both the space needed for the input and the space required for the auxiliary variables used in the algorithm.
- Space complexity is also expressed using Big O notation.
Coding
- Coding is the process of translating an algorithm into a programming language to create a software program.
- It involves writing a set of instructions in a specific syntax that a computer can understand and execute.
Process of Coding
- Choose a Programming Language: Select a high-level programming language that is suitable for the project. Popular languages include Python, Java, C++, and JavaScript.
- Set Up the Development Environment: Configure the necessary tools and software required for coding, such as text editors, integrated development environments (IDEs), and compilers.
- Write the Code: Translate the algorithm into code by following the syntax and rules of the chosen programming language. Break down the code into functions or modules for better organization.
- Test the Code: Run the code to check for errors and ensure it produces the expected output. Debug any issues that arise during testing.
- Optimize the Code: Review the code for efficiency and make necessary improvements to enhance performance and reduce resource usage.
- Document the Code: Add comments and documentation to explain the code's functionality and usage for future reference.
Decomposition
Sometimes, a problem can be too complicated, and its solution isn't obvious right away. In such situations, we need to break it down into simpler parts. Let's revisit the example of the Railway reservation system. Instead of trying to design the entire system at once, we can focus on creating different components and making sure they work well together.
The main idea behind solving a complex problem through decomposition is to divide it into smaller sub-problems, which are easier to tackle than the original issue. Once we solve these sub-problems, we can combine their solutions to get the answer to the bigger problem.
For instance, in a Railway reservation system, we can break down the problem into various aspects like:
- Trains' information: Days, timings, stations, classes, and berths
- Reservation details: Booking status, availability, waiting list, cancellation, and refund
- Staff and security information
- Railway infrastructure details
- Billing services
- Food service options
Breaking a complex problem into sub-problems allows for detailed examination of each part. Different teams or individuals can work on these sub-problems independently, and it's beneficial to assign specific sub-problems to teams with expertise in those areas.
Decomposition can be applied to various real-life challenges such as:
- Solving mathematical and scientific problems
- Organizing events in schools
- Weather forecasting
- Delivery management systems
|
33 docs|11 tests
|
FAQs on Introduction to Problem Solving Chapter Notes - Computer Science for Class 11 - Humanities/Arts
| 1. What are the key steps involved in problem-solving? |  |
| 2. What is an algorithm and how is it represented? |  |
| 3. How does flow control work in algorithms? |  |
| 4. Why is it important to verify algorithms? |  |
| 5. What is the significance of algorithm comparison in problem-solving? |  |




















