Class 10 Exam > Class 10 Notes > Mathematics Class 10 ICSE > Revision Notes: Geometric Progression
Revision Notes: Geometric Progression | Mathematics Class 10 ICSE PDF Download
Important Terms
- A sequence is an arrangement of numbers in a definite order according to some rule.
- The various numbers occurring in a sequence are called its terms. We denote the terms of a sequence by a1, a2, a3… etc. Here, the subscripts denote the positions of the terms. In general, the number at the nth place is called the nth term of the sequence and is denoted by an. The nth term is also called the general term of the sequence.
- A sequence having a finite number of terms is called a finite sequence.
- A sequence which do not have a last term and which extends indefinitely is known as an infinite sequence.
Geometric Progression
A sequence is said to be in geometric progression or G.P., if the ratio of any term to its preceding term is same throughout. Constant Ratio is common ratio denoted by ‘r’.
General Term of a G.P.
The general term of a G.P. is given by
tn = arn –1
where ‘a’ is the first term and ‘r’ is the common ratio.
Properties of G.P.
- The ratio between the consecutive terms of a G.P. is always the same.
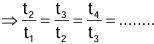
- rth term from the beginning x rth term from the end = constant = First term x Last term
- If a, b and c are in G.P,
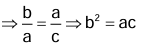
- In a G.P. if the terms at equal distances are taken, these terms are also in G.P.
- If each term of a G.P. be multiplied or divided by the same non-zero number, the resulting series is also a G.P.
- The series obtained by taking the reciprocals of the terms of a G.P. is also a G.P.
- If each term of a G.P. is raised to the same non-zero number, the resulting series is also a G.P.
- If the corresponding terms of two different G.P.s are multiplied/divided together, the resulting series, so obtained, is also a G.P.
Sum of n terms of a G.P.
Sn = a + ar + ar² + … + arn-1
Case I: r = 1
Sn = a + a + a + … + to n terms = na
Case II: r < 1
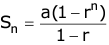
Case III: r > 1
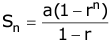
Sum of Infinite terms of a G.P.
Sum of infinite terms in G.P. , =
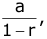if |r| < 1Geometric Mean Between Numbers a and b
If a and b are two positive numbers then a, G, b are in G.P.
⇒ G2 = ab
⇒ G = √(ab)
Three or More Terms in G.P.
Number of terms is three: a/r, a, ar
Number of terms is four: a/(r3), a/r, a, ar3
Number of terms is five:
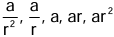
and so on.
The document Revision Notes: Geometric Progression | Mathematics Class 10 ICSE is a part of the Class 10 Course Mathematics Class 10 ICSE.
All you need of Class 10 at this link: Class 10
|
74 videos|328 docs|30 tests
|
FAQs on Revision Notes: Geometric Progression - Mathematics Class 10 ICSE
| 1. What is a geometric progression (GP)? |  |
Ans. A geometric progression (GP) is a sequence of numbers where each term after the first is found by multiplying the previous term by a fixed, non-zero number called the common ratio. For example, in the sequence 2, 6, 18, 54, the common ratio is 3 because each term is obtained by multiplying the previous term by 3.
| 2. How do you find the nth term of a geometric progression? | |
Ans. The nth term of a geometric progression can be found using the formula: \( a_n = a \cdot r^{(n-1)} \), where \( a \) is the first term, \( r \) is the common ratio, and \( n \) is the term number. For example, if the first term is 5 and the common ratio is 2, the 4th term would be \( 5 \cdot 2^{(4-1)} = 5 \cdot 8 = 40 \).
| 3. What is the sum of the first n terms of a geometric progression? | |
Ans. The sum \( S_n \) of the first \( n \) terms of a geometric progression can be calculated using the formula: \( S_n = a \cdot \frac{(1 - r^n)}{(1 - r)} \) when \( r \neq 1 \), where \( a \) is the first term and \( r \) is the common ratio. For example, for a GP with a first term of 3 and a common ratio of 2, the sum of the first 4 terms would be \( 3 \cdot \frac{(1 - 2^4)}{(1 - 2)} = 3 \cdot \frac{(1 - 16)}{-1} = 3 \cdot 15 = 45 \).
| 4. Can a geometric progression have a negative common ratio? | |
Ans. Yes, a geometric progression can have a negative common ratio. In this case, the terms will alternate between positive and negative values. For example, if the first term is 4 and the common ratio is -2, the sequence will be 4, -8, 16, -32, and so on.
| 5. How can geometric progressions be applied in real life? | |
Ans. Geometric progressions are used in various real-life scenarios, such as calculating compound interest in finance, modeling population growth, or analyzing exponential decay in natural sciences. For instance, if an investment grows at a fixed percentage rate annually, the value of the investment over time can be represented as a geometric progression.
About this Document
4.67/5
Rating
Oct 24, 2025
Last updated
Document Description: Revision Notes: Geometric Progression for Class 10 2025 is part of Mathematics Class 10 ICSE preparation.
The notes and questions for Revision Notes: Geometric Progression have been prepared according to the Class 10 exam syllabus. Information about Revision Notes: Geometric Progression covers topics
like and Revision Notes: Geometric Progression Example, for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Revision Notes: Geometric Progression.
Introduction of Revision Notes: Geometric Progression in English is available as part of our Mathematics Class 10 ICSE
for Class 10 & Revision Notes: Geometric Progression in Hindi for Mathematics Class 10 ICSE course.
Download more important topics related with notes, lectures and mock test series for Class 10
Exam by signing up for free. Class 10: Revision Notes: Geometric Progression | Mathematics Class 10 ICSE
Description
Full syllabus notes, lecture & questions for Revision Notes: Geometric Progression | Mathematics Class 10 ICSE - Class 10 | Plus excerises question with solution to help you revise complete syllabus for Mathematics Class 10 ICSE | Best notes, free PDF download
Information about Revision Notes: Geometric Progression
In this doc you can find the meaning of Revision Notes: Geometric Progression defined & explained in the simplest way possible. Besides explaining types of
Revision Notes: Geometric Progression theory, EduRev gives you an ample number of questions to practice Revision Notes: Geometric Progression tests, examples and also practice Class 10
tests
Related Searches
Objective type Questions
,MCQs
,Free
,past year papers
,mock tests for examination
,Sample Paper
,Summary
,Revision Notes: Geometric Progression | Mathematics Class 10 ICSE
,Viva Questions
,Revision Notes: Geometric Progression | Mathematics Class 10 ICSE
,Extra Questions
,Semester Notes
,Revision Notes: Geometric Progression | Mathematics Class 10 ICSE
,Important questions
,Exam
,shortcuts and tricks
,video lectures
,ppt
,practice quizzes
,study material
,Previous Year Questions with Solutions
;
Additional Information about Revision Notes: Geometric Progression for Class 10 Preparation
Revision Notes: Geometric Progression Free PDF Download
The Revision Notes: Geometric Progression is an invaluable resource that delves deep into the core of the Class 10 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Revision Notes: Geometric Progression now and kickstart your journey towards success in the Class 10 exam.
Importance of Revision Notes: Geometric Progression
The importance of Revision Notes: Geometric Progression cannot be overstated, especially for Class 10 aspirants.
This document holds the key to success in the Class 10 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Revision Notes: Geometric Progression
Revision Notes: Geometric Progression Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Revision Notes: Geometric Progression.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Revision Notes: Geometric Progression Notes on EduRev are your ultimate resource for success.
Revision Notes: Geometric Progression Class 10 Questions
The "Revision Notes: Geometric Progression Class 10 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 10 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Revision Notes: Geometric Progression on the App
Students of Class 10 can study Revision Notes: Geometric Progression alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Revision Notes: Geometric Progression,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Revision Notes: Geometric Progression is prepared as per the latest Class 10 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup