Class 10 Exam > Class 10 Notes > Mathematics Class 10 ICSE > Revision Notes: Measures of Central Tendency - Mean, Median and Mode
Revision Notes: Measures of Central Tendency - Mean, Median and Mode | Mathematics Class 10 ICSE PDF Download
The numerical expressions which represent the characteristics of a group are called Measures of Central Tendency.
Three measures of central tendency are:
i. Mean
ii. Median
iii. Mode
Arithmetic Mean
The arithmetic mean is the sum of all observations in the data divided by the number of observations.’
Arithmetic Mean of n numbers x1, x2, x3, ... , xn =
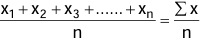
The Greek letter ∑ (called sigma) represents the sum of numbers.
The arithmetic mean may be computed by any of the following methods:
i. Direct method
ii. Short-cut method
iii. Step-deviation method
Direct method
If a variable X takes values x1, x2, x3 .... , xn with corresponding frequencies f1, f2, f3 ,... fn respectively, then the arithmetic mean of these values is given by,
Mean =
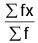
Short-cut method
This method is used to overcome the difficulty faced in calculations where large quantities are involved.
Let x1, x2 ,......., xn be values at a variable x with corresponding frequencies f1, f2,.......,fn respectively.
Takingthe derivative at an arbitrary point ‘A’, we have
Mean = A +
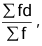 where A = Assumed mean and d = x – A
where A = Assumed mean and d = x – AStep-deviation method
Sometimes, during the application of the shortcut method for finding the arithmetic mean of the derivative d is divisible by a common number i (say).
In such cases, arithmetic is reduced to a great extent by taking ui = t =
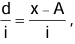 then
thenMean = A +
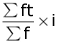
Median
- Median is the value of the middle observation(s).
- The median is to be calculated only after arranging the data in ascending order or descending order.
To find the Median for raw and arrayed data
To find the median of raw data, arrange the raw data in ascending or descending order. Then, observe the number of variables in the data. Let it be n. Then find the median as follows.
(a) If n is odd, then the
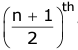 variate is the median.
variate is the median.(b) If n is even, then the mean of the nth/2 and
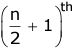 variates is the median, i.e.,
variates is the median, i.e.,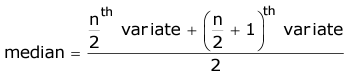
Median for tabulated data
- Construct a cumulative frequency distribution table
- If there are n terms in the given distribution, then use the table to find the value of (n/2)th or
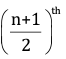 term, which is the median of the given distribution.
term, which is the median of the given distribution.
Median for grouped data (both continuous and discontinuous)
- Draw a cumulative frequency curve (Ogive).
- If there are n terms in the given distribution, then use the ogive to find the value of (n/2)th or
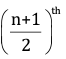 term, which is the median of the given distribution.
term, which is the median of the given distribution.
Mode
- The mode of a statistical dataset is the value of that variate which has the maximum frequency.
- The mode for ungrouped data is the value that occurs most often.
- The mode may be greater than, less than or even equal to the mean.
Mode for tabulated data
- In the case of a grouped frequency distribution, a class with the maximum frequency is called as the modal class.
To find the mode of a group frequency distribution (using a histogram)
Steps:
- Draw a histogram of the given distribution.
- Inside the highest rectangle, which represents the maximum frequency (or modal class), draw two lines AC and BD diagonally from the upper corners C and D of adjacent rectangles.
- The point of intersection is M. Now ML is perpendicular to the horizontal axis.
- The value of point L on the horizontal axis represents the value of the mode.

Quartiles
- The three variates which divide the data of a distribution in four equal (quarters) are called quartiles.
- If there are n terms arranged in an ascending order, then
Lower Quartile (Q1) = (n/4)th term, if n is even or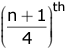 term, if n is odd.
term, if n is odd. - If there are n terms arranged in an ascending order, then
Upper Quartile (Q3) = (3n/4)th term, if n is even or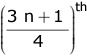 term, if n is odd.
term, if n is odd. - Q2 is called the middle quartile, and the median is the second quartile.
- Lower Quartile is the value which cuts off the lowest 25% of the data. It is denoted by Q1.
- Upper Quartile is that value which cuts off the highest 25% of the data. It is denoted by Q3 and is the 75th percentile.
- The difference between the greatest variate and the smallest variate in a distribution is called the range of the distribution.
- The difference between the lower quartile and the upper quartile is the Interquartile Range, and it is equal to Q3 - Q1.
- The interquartile range is always positive, as Q3 > Q1
- Semi-interquartile range is equal to 1/2(Q3 - Q1).
The document Revision Notes: Measures of Central Tendency - Mean, Median and Mode | Mathematics Class 10 ICSE is a part of the Class 10 Course Mathematics Class 10 ICSE.
All you need of Class 10 at this link: Class 10
|
74 videos|328 docs|30 tests
|
FAQs on Revision Notes: Measures of Central Tendency - Mean, Median and Mode - Mathematics Class 10 ICSE
| 1. What is the mean in statistics and how is it calculated? |  |
Ans. The mean, often referred to as the average, is a measure of central tendency that summarizes a set of values. It is calculated by adding all the numbers in a data set and then dividing the sum by the total number of values. For example, for the data set {2, 4, 6, 8}, the mean would be (2 + 4 + 6 + 8) / 4 = 5.
| 2. What are the advantages and disadvantages of using the mean as a measure of central tendency? |  |
Ans. The advantages of using the mean include its simplicity and the fact that it uses all values in the data set, providing a comprehensive overview. However, its disadvantages include sensitivity to extreme values (outliers), which can skew results. For example, in the data set {1, 2, 3, 100}, the mean is heavily influenced by the outlier 100.
| 3. How does the mean differ from other measures of central tendency, such as median and mode? |  |
Ans. The mean is the average of all values, the median is the middle value when data is ordered, and the mode is the most frequently occurring value in a data set. For instance, in the set {1, 2, 2, 3, 4}, the mean is 2.4, the median is 2, and the mode is 2. Each measure provides different insights depending on the distribution of the data.
| 4. When should the mean be used instead of the median or mode? |  |
Ans. The mean should be used when the data is symmetrically distributed without outliers, as it provides a more accurate representation of the data set. In contrast, the median is preferred in skewed distributions or when outliers are present, as it is less affected by extreme values. The mode is useful when identifying the most common item in categorical data.
| 5. Can the mean be used for all types of data, or are there restrictions? |  |
Ans. The mean can be calculated for interval and ratio data, but it is not suitable for nominal or ordinal data. For example, calculating the mean of categories like colors or ranks does not provide meaningful information. Therefore, it is important to choose the appropriate measure of central tendency based on the type of data being analyzed.
Related Searches















