Class 10 Exam > Class 10 Notes > Mathematics Class 10 ICSE > Revision Notes: Probability
Revision Notes: Probability | Mathematics Class 10 ICSE PDF Download
Important Concepts
- Probability is a concept which numerically measures a degree of uncertainty and therefore of certainty of the occurrence of events.
- An action which results in one of several outcomes is called an experiment.
- An experiment is called random if it has more than one possible outcome and cannot be predicted or determined in advance. i.e. Tossing a coin, Rolling a die.
- The set of possible outcomes or the totality of all possible outcomes of an experiment constitutes the sample space.
- An outcome of a random experiment is called an event.
- The outcomes in an experiment which are favourable to an event which we are interested are called favourable out comes and all other outcomes are known as unfavourable outcomes.
- The sum of the favourable and unfavourable outcomes is equal to the exhaustive number of events in experiment.
- If there is no reason for any one outcome to occur is preference to any other outcome then we can say that the outcomes are equally likely.
- 4 aces, 4 queens, 4 kings, and 4 jacks are called face cards.
Measurement of Probability
- Probability of an Event = (number of outcomes favourable to event)/(number of all possible outcomes of the experiment)
⇒ P(E) = n(E)/n(S) - When the probability is based on an actual experiment, it is called an empirical probability
- When a repetition of an experiment can be avoided for calculating the exact probability, the probability so obtained is called classical or theoretical probability.
- In theoretical probability, the outcomes are equally likely.
- For any event E, the event of non-occurrence of E is called its complementary event and is denoted by E.
- E and
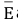 are called complementary events.
are called complementary events. - The sum of probabilities of an event and its complementary event is always 1.
- Impossible event: If the probability of an event = 0, the event is called an impossible event.
- Sure event: If the probability of an event = 1, the event is called a certain event or a sure event.
- Probability of any event can never be less than 0 or more than 1.
Important concepts
- Tossing of two coins simultaneously or tossing one coin twice, gives the same outcomes.
- In a coins is tossed n times or n coins are tossed simultaneously, the number of possible outcomes = 2n.
- Rolling a dice two times gives the same result as rolling two dice simultaneously.
- If a dice is rolled n times or n-dice are rolled simultaneously, the number or outcomes = 6n .
The document Revision Notes: Probability | Mathematics Class 10 ICSE is a part of the Class 10 Course Mathematics Class 10 ICSE.
All you need of Class 10 at this link: Class 10
|
74 videos|198 docs|30 tests
|
FAQs on Revision Notes: Probability - Mathematics Class 10 ICSE
| 1. What is the basic definition of probability? |  |
Ans. Probability is a branch of mathematics that deals with the likelihood of events occurring. It quantifies uncertainty and is expressed as a number between 0 and 1, where 0 indicates impossibility and 1 indicates certainty. The probability of an event can be calculated using the formula: Probability (P) = Number of favorable outcomes / Total number of outcomes.
| 2. How do you calculate the probability of a single event? |  |
Ans. To calculate the probability of a single event, you can use the formula P(Event) = Number of favorable outcomes / Total number of outcomes. For example, if you want to find the probability of rolling a 3 on a six-sided die, the number of favorable outcomes is 1 (only one side shows a 3) and the total number of outcomes is 6 (the six sides of the die). Therefore, P(rolling a 3) = 1/6.
| 3. What is the difference between theoretical probability and experimental probability? |  |
Ans. Theoretical probability is based on the expected outcomes of an event based on mathematical reasoning, while experimental probability is based on the actual results of an experiment or observation. Theoretical probability is calculated using the formula mentioned earlier, whereas experimental probability is calculated by conducting trials and recording the outcomes. For example, if you flip a coin 100 times and it lands on heads 45 times, the experimental probability of getting heads is 45/100.
| 4. Can you explain the concept of complementary events in probability? |  |
Ans. Complementary events are two outcomes of an event that cover all possible outcomes. For any event A, the complement of A (denoted as A') is the event that A does not occur. The probability of A and its complement A' always adds up to 1. Mathematically, this is expressed as P(A) + P(A') = 1. For example, if the probability of raining tomorrow is 0.3, then the probability of not raining (the complement) is 1 - 0.3 = 0.7.
| 5. What is the significance of the Law of Large Numbers in probability? |  |
Ans. The Law of Large Numbers states that as the number of trials in an experiment increases, the experimental probability of an event will converge to its theoretical probability. This principle highlights the importance of conducting a large number of trials to obtain reliable estimates of probability. For example, if you flip a coin many times, the proportion of heads and tails will approach 50% as the number of flips increases.
Related Searches















