Proof of Theorems: Circles | Mathematics (Maths) Class 10 PDF Download

Theorem 1: Tangent at any point of a circle is perpendicular to the radius through the point of contact.

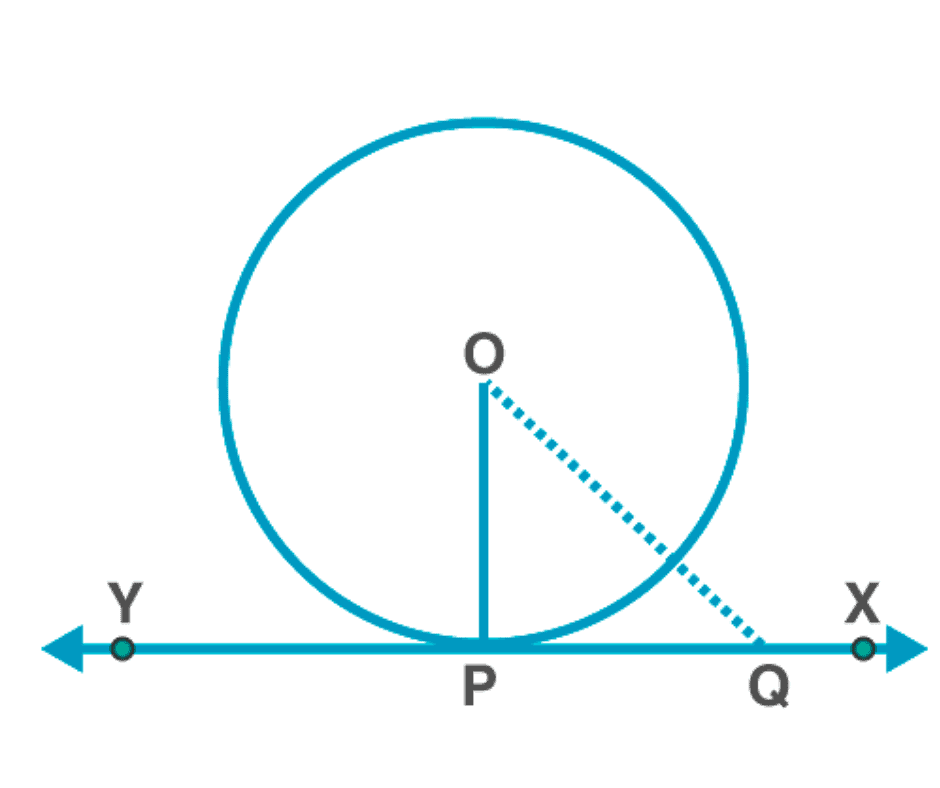
According to the theorem, O is the centre and OP⊥XY.
Proof: Let Q be a point on XY.
Construction: Connect OQ.
Suppose it touches the circle at R.
Hence,
OQ > OR
OQ > OP (as OP = OR, radius).
The same will be the case for all other points on the circle.
Hence, OP is the smallest line that connects XY.

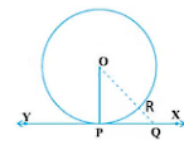
Thus, OP is the smallest line that connects XY, and the smallest line is perpendicular.
∴ OP ⊥ XY

Note:
1. By the theorem above, we can also conclude that at any point on a circle, there can be one and only one tangent.
2. The line containing the radius through the point of contact is also sometimes called the ‘normal’ to the circle at the point.

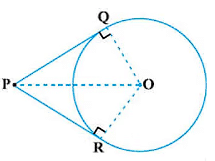
Theorem 2: The lengths of tangents drawn from an external point to a circle are equal.

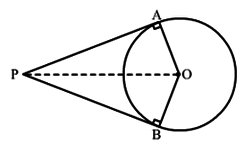
Given:
Let the circle be with center O, and P be a point outside the circle.
PQ and PR are two tangents to the circle intersecting at points Q and R respectively.

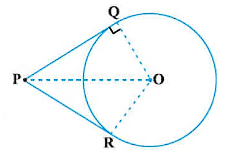
To prove:
Lengths of tangents are equal, i.e., PQ = PR.
Construction:
Join OQ, OR, and OP.
Proof:
As PQ is a tangent,
OQ ⊥ PQ
(Tangent at any point of a circle is perpendicular to the radius through the point of contact).
So, ∠OQP = 90°
Hence, ΔOQP is a right triangle.
Similarly,
PR is a tangent,
& OR ⊥ PR
(Tangent at any point of a circle is perpendicular to the radius through the point of contact).
So, ∠ORP = 90°
Hence, ΔORP is a right triangle.
Using Pythagoras theorem:
(Hypotenuse)² = (Height)² + (Base)²

In right-angled triangle ΔOQP:
OP² = PQ² + OQ²
OP² − OQ² = PQ²
PQ² = OP² − OQ² …(1)
In right-angled triangle ΔORP:
OP² = PR² + OR²
OP² = PR² + OQ² (As OQ = OR, both are radii)
OP² − OQ² = PR²
PR² = OP² − OQ² …(2)

Note:

1. The theorem can also be proved by using the Pythagoras Theorem as follows:
PA² = OP² – OA² = OP² – OB² = PB² (As OA = OB) which gives PA = PB.
2. Note also that ∠ OPA = ∠ OPB. Therefore, OP is the angle bisector of ∠ APB,i.e., the centre lies on the bisector of the angle between the two tangents.