Case Based Questions: Pair of Linear Equations in Two Variables | Mathematics (Maths) Class 10 PDF Download

Q1: Read the source below and answer the questions that follow:

i. Represent the following information algebraically (in terms of x and y). (1 mark)
ii. What is the prize amount for hockey? (1 mark)
iii. Prize amount on which game is more and by how much? (1 mark)
iv. What will be the total prize amount if there are 2 students each from two games? (1 mark)

Ans: 
i. For Hockey, the amount given to per student =  x
For cricket, the amount given to per student = y
From the question,
5x + 4y =9500    (i)
4x + 3y = 7370   (ii)
ii. Multiply (1) by 3 and (2) by 4 and then subtracting, we get
15x + 12y- (16x + 12y) = 28500 - 29480
⇒ - x = - 980
⇒ x = ₹980
The prize amount given for hockey is Rs. 980 per student
iii. Multiply (1) by 4 and (2) by 5 and then subtracting, we get
20x + 16y- 20x - 15y = 38000 - 36850
⇒ y = 1150
The prize amount given for cricket is more than hockey by (1150 - 980) = 170.
iv. Total prize amount = 2 x 980 + 2 x 1150
= Rs. (1960 + 2300) = Rs. 4260

Clear all your Class 10 doubts with EduRev Join for Free

Join for Free

Q2: Read the source below and answer the questions that follow:

Ans:
i. Let x and y be the number of rides on the giant wheel and number of hoopla respectively played by Akhila. 
Then, according to the given condition,
y = x/2 and 3x + 4y = 20
.. The given situation can be algebraically represented by the following pair of the linear equations are
x-2y=0 ...(1) and 3x+4y=20...(2)
ii. Put x=2y in eq. (2), we get 
3(2y) + 4y = 20 
= 10y=20 
= y = 2 
:- x = 2 x 2 = 4 
Hence, intersection point of two lines is (4, 2).
iii. Table for equation x-2y=0 is:
i.e., the lines passes through the origin.
iv. Table for equation 3x + 4y = 20 is: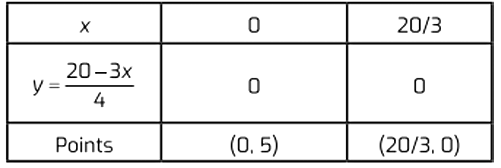
i.e., the intersection points of the line on X and Y-axes are (20/3, 0) and (0, 5).

RD Sharma Test: Pair of Linear Equations in Two Variables

Start Test

Start Test

Q3: Read the source below and answer the questions that follow:

i. Find the coordinates of the points on X-axis, where the two lines, plotted on a graph paper intersect the X-axis. (1 mark)
ii. Find the value of k for which the system of equations x + y - 4 = 0 and 2x+ky = 3 has no solution. (1 mark)
iii. Find the dimensions of the rectangle. (2 mark)
Or
iii. If the graphs of the equations in the given situation are plotted on the same graph paper, then lines will intersect. Check whether given statement is True/False. (1 mark)

Ans:
i. The points where the two lines will intersect the X-axis can be found by putting y = 0 in both the equations, 
as the y-coordinate of all points lying on the X-axis is zero. 
Putting y = 0 in the equations x - y = 4 and 3x-y=24, 
we get x=4 and x = 8, respectively. 
Therefore, the points are (4, 0) and (8,0). 
ii. For no solution
a₁/a₂ = b₁/b₂ ≠ c₁/c₂ 
⇒ 1/2 = 1/k ≠ 4/3 
⇒ k = 2
iii. Let the length and breadth of the rectangular garden be denoted by xm and y m respectively. The area of the rectangular garden = xy sq. m. According to the question, (x+2) (y-2)=xy-12
Simplifying the above equations, we get
xy-2x+2y-4=xy-12
= -2x+2y=8
= xy=4 ...(1)
And (x-1) (y+3)=xy+21
xy+3x-3y + 21
= 3x-y=24 ...(2)
Let us now solve the eqs. (1) and (2) by the method of substitution.
From eq. (1), x= y +4 ...(3)
Substituting in eq. (2).
3(y+4)-y=24
= 3y+12-y=24
= 2y=12)y=6
Substituting y = 6 in eq. (3), x=6+4=10
Therefore, length = 10 m and breadth = 6 m.
Let us now solve the eqs. (1) and (2) by the method of substitution.
From eq. (1), x= y +4 ...(3)
Substituting in eq. (2).
3(y+4)-y=24
= 3y+12-y=24
= 2y=12)y=6
Substituting y = 6 in eq. (3), x=6+4=10
Therefore, length = 10 m and breadth = 6 m.
Or
iii. We can find whether lines will be intersecting, coincident or parallel, by calculating the ratios of the coefficients of the pair of linear equations. 
As the two equations are given by 
x - y = 4 and 3x - y = 24 
Let us calculate the ratios of their coefficients

Q4: Read the source below and answer the questions that follow:

The cost of three balloon shooting games exceeds the cost of four ring games by 4. Also, the total cost of three balloon shooting games and four ring games is 20. 

i. Taking the cost of one ring game to be *x and that of one balloon game as y, find the pair of linear equations describing the given statement. (1 mark) 
ii. Find the total cost of five ring games and eight balloon games. (1 mark)
iii. Find the cost of one balloon game. (1 mark)
iv. Cost of which game is more and by how much? (1 mark)

Ans:
i. Given, the cost of one ring game = x and cost of one balloon game = y. 
According to the question, 
3y=4x+4 or 4x-3y=-4 ...(1) and 4x+3y=20 ...(2) 
ii. Total cost of five ring games and eight balloon games=5x+8y =5x2+8x4 = 10 +32 =42. 
iii. Solving the equations 4x-3y=-4 and 4x + 3y = 20 by the method of substitution. 
From eq. (1). 4x=3y-4 ...(3) Substituting the value of 4x in eq. 
(2), (3y-4)+3y=20 = 6y-4=20 = 6y=24 = y= 4 .. 
Cost of one balloon game = Rs 4.
iv. Now, substituting y = 4 in eq. (3). 
4x=3x4-4-8 ⇒ x=2 
Therefore, cost of one ring game = Rs2 
Thus cost of one balloon game is more and by Rs (4-2)=Rs2