Case Based Questions: Arithmetic Progressions | Mathematics (Maths) Class 10 PDF Download
Q1: Read the source below and answer the questions that follow:
In an examination hall, the examiner makes students sit in such a way that no students can cheat from other student and make no student sit uncomfortably. So, the teacher decides to mark the numbers on each chair from 1, 2, 3, ...... There are 25 students and each student is seated at alternate position in examination room such that the sequence formed is 1, 3, 5,...
i. What type of sequence is formed, to follow the seating arrangement of students in the examination room? (1 mark)
ii. Find the seat number of the last student in the examination room. (1 mark)
iii. Find the seat number of 10th vacant seat in the examination room. (1 mark)
iv. Which number of student will seat on the 27th seat number. (1 mark)
Ans:
i. Given, seating arrangement of students in the examination room is 1, 3, 5,.
Here, a₁ = 1,a2=3,a3 = 5, ......
Now, a2-a₁=3-1=2
a3-a2-5-3=2
Here, common difference is same, so given sequence is the type of Arithmetic progression.
ii. Given, a=1, d=3-1-2 and n= 25
Tn = a+ (n-1)d
There are 25 students.
.. T25=1+(25-1)2=1+24x2=49
Hence, last student will sit on the 49th seat number.
iii. The sequence of vacant seats are as follows,
2, 4, 6.......... 48.
Here, a 2, d=4-2-6-4-2
The 10th vacant seat will be
T10 = a + (10-1)d (;- Tn+ (n-1)d)
=2+9x2=2+18=20
Hence, the 10th vacant seat number is 20.
iv. The sequence of seating arrangement of students in the examination room is
1,3,5,7,
Let nth number of student will seat on 27th seat number.
Here,
a =1, d = 3 - 1 - 2 and Tn = 27
:- Tn = a + (n - 1)d
:- 27 = 1 + (n - 1) (2)
⇒ n - 1 = 26 / 2
⇒ n = 13 + 1 = 14
Q2: Read the source below and answer the questions that follow:
In a pathology lab, a culture test has been conducted. In the test, the number of bacteria taken into consideration in various samples are all three‑digit numbers divisible by 7, taken in order.
i. How many bacteria are considered in the seventh sample? (1 mark)
ii. How many samples should be taken into consideration? (1 mark)
iii. Find the total number of bacteria in the first 15 samples. (1 mark)
iv. Find the number of samples in which the sum of bacteria is 840. (1 mark)
Ans:
We know the smallest three-digit number divisible by 7 is 105 and the largest is 994.
So, the numbers are: 105, 112, 119, …, 994.
Here, first term a = 105, common difference d = 7, and last term aₙ = 994.
i. Seventh sample
a₇ = a + (7 − 1)d
= 105 + 6 × 7
= 105 + 42 = 147
ii. Total number of samples
aₙ = a + (n − 1)d
994 = 105 + (n − 1) × 7
n − 1 = (994 − 105) ÷ 7 = 889 ÷ 7 = 127
n = 127 + 1 = 128
iii. Total bacteria in first 15 samples
S₁₅ = (15 ÷ 2) [2a + (15 − 1)d]
= (15 ÷ 2) [210 + 14 × 7]
= (15 ÷ 2) [210 + 98]
= (15 ÷ 2) × 308
= 15 × 154 = 2310
iv. Number of samples for sum = 840
Sₙ = (n ÷ 2) [2a + (n − 1)d]
840 = (n ÷ 2) [210 + 7n − 7]
840 = (n ÷ 2) (7n + 203)
1680 = n(7n + 203)
7n² + 203n − 1680 = 0
n² + 29n − 240 = 0
Discriminant = 29² + 4 × 240 = 841 + 960 = 1801 (not a perfect square)
No positive integer solution ⇒ No exact number of samples has a total of 840 bacteria.
Q3: Read the source below and answer the questions that follow:
India is competitive manufacturing location due to the low cost of manpower and strong technical and engineering capabilities contributing to higher quality production runs. The production of TV sets in a factory increases uniformly by a fixed number every year. It produced 16000 sets in 6th year and 22600 in 9th year.
i. In which year, the production is Rs 29,200. (1 mark)
ii. Find the difference of the production during 7th year and 4th year. (1 mark)
iii. Find the production during 8th year. (1 mark)
iv. Find the production during first 3 years. (1 mark)
Ans:
Given that, the production of TV sets in a factory increases uniformly by a fixed number every year i.e., production of TV sets in every year form an AP. Let the first term and common difference of this AP be 'a' and 'd' respectively. According to the question, the factory produced 16000 sets in 6th year and 22600 in 9th year.
i.e.. a6= =a + (6 - 1)d = 16000
⇒ a + 5d = 16000 ...(1)
and a9 = a + (9 - 1)d = 22600
⇒ a + 8d = 22600 ...(2)
Subtract eq (1) from eq (2), we get
(a + 8d) - (a + 5d) = 22600 - 16000
⇒ 3d = 6600
⇒ d = 6600 / 3 = 2200
put the value of 'd' in eq. (1), we get
⇒ a + 5 (2200) = 16000
⇒ a = 16000 - 11000
⇒ a = 5000.
i. Let nth year, the production is,
aₙ = 29,200
⇒ a + (n - 1)d = 29200
⇒ 5000 + (n - 1) (2200) = 29200
⇒ (n - 1) = 24200 / 2200 = 11
∴ n = 11 + 1 = 12
Hence, in 12th year, the production is * 29,200.
ii. Now, the production during 7th year is
a7 = a + (7 - 1)d
= 5000 + 6(2200)
= 5000 + 13200 = 18200
and the production during 4th year is
a4 = a + (4 - 1)d
= 5000 + 3(2200)
= 5000 + 6600 = 11600.
.. The difference of the production during 7th year and 4th year = 18200-11600-6600.
iii. The production during 8th year is
a8 = a + (8 - 1)d
= 5000 + 7 x 2200
= 5000 + 15400
- 5000 + 15400
= 20400.
iv. The production during first 3 years is
S₃ = (3 / 2) [2 × 5000 + (3 - 1)(2200)]
= 3 (5000 + 2200)
= 3 × 7200 = 21600.
Q4: Read the source below and answer the questions that follow:
Aahana being a plant lover decides to convert her balcony into beautiful garden full of plants. She bought few plants with pots for her balcony. She placed the pots in such a way that number of pots in the first row is 2, second row is 5, third row is 8 and so on.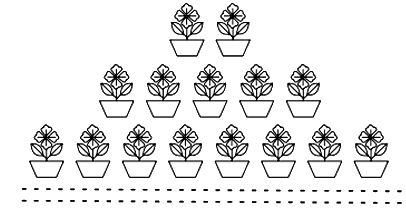
i. Find the number of pots placed in the 10th row. (1 mark)
ii. Find the difference in the number of pots placed in 5th row and 2nd row. (1 mark)
iii. If Aahana wants to place 100 pots in total, then find the total number of rows formed in the arrangement. (1 mark)
iv. If Aahana has sufficient space for 12 rows, then how many total number of pots are placed by her with the same arrangement?
(1 mark)
Ans:
Given that, Aahana placed the pots in such a way that number of pots in the first row is 2 second row is 5, third row is 8 and so on. Such a pattern form a sequence:
2,5,8,...
Here, 5 - 2 - 8 - 5 = 3 (Constant)
So, the above sequence form an AP.
Let the first term and common difference of this AP.
be 'a' and 'd' respectively.
Here,
a = 2 and d = 3
i. The number of pots placed in the 10th row is,
910 = a + (10 - 1)d
= 2 + 9(3)
=2 + 27 = 29.
ii. The number of pots placed in 5th row is,
a5 = a + (5 - 1)d
=2 + 4 x 3 = 2 + 12 = 14.
and the number of pots placed in 2nd row is,
a₂ = a + (2 - 1)d
= a + d = 2 + 3 = 5.
.. The difference in the number of pots placed in 5th row and 2nd row =14 - 5 = 9.
iii. Let 'n' number of rows formed in the arrangement
Here, Sₙ = 100, a = 2 and d = 3
∴ 100 = (n / 2) {2 × 2 + (n - 1)(3)}
⇒ 200 = n (4 + 3n - 3)
⇒ 3n² + n - 200 = 0
⇒ 3n² + 25n - 24n - 200 = 0 (By splitting the middle terms)
⇒ n(3n + 25) - 8(3n + 25) = 0
⇒ (3n + 25) (n - 8) = 0
⇒ 3n + 25 = 0 or n - 8 = 0
⇒ n = -25/3 , 8.
But n cannot be negative because n is a natural number.
∴ n = 8
So, required number of rows is 8.
iv. Given, n = 12, a = 2 and d = 3
∴ Sₙ = (n / 2) {2a + (n - 1)d}
∴ S₁₂ = (12 / 2) {2 × 2 + (12 - 1)3}= 6 (4 + 33) = 222
So, the total number of pots are 222, placed by her with the same arrangement.
|
127 videos|584 docs|79 tests
|
FAQs on Case Based Questions: Arithmetic Progressions - Mathematics (Maths) Class 10
| 1. What is an arithmetic progression and how is it defined? |  |
| 2. How can I find the nth term of an arithmetic progression? |  |
| 3. What is the formula for the sum of the first n terms of an arithmetic progression? |  |
| 4. Can you give an example of an arithmetic progression? |  |
| 5. How do you determine if a sequence is an arithmetic progression? |  |






















