Case Based Questions: Triangles | Mathematics (Maths) Class 10 PDF Download

Q1: Read the source below and answer the questions that follow:

Anika is studying in class X. She observe two poles DC and BA. The heights of these poles are x m and y m respectively as shown in figure: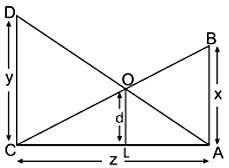
These poles are z m apart and O is the point of intersection of the lines joining the top of each pole to the foot of opposite pole and the distance between point O and L is d. Few questions came to his mind while observing the poles. 

i. Which similarity criteria is applicable in ∆ACAB and CLO? (1 mark)
ii. If x=y, prove that BC: DA = 1 : 1. (1 mark)
iii. If CL = a, then find a in terms of x, y and d. (1 mark)
iv. If AL = b, then find b in terms of x, y and d. (1 mark)

Ans:
i. In ΔCAB and ΔCLO, we have
∠CAB = ∠CLO = 90°
∠C = ∠C (common)
.. By AA similarity criterion,
ΔCAB ~ ΔCLO
ii. In ΔDCA and ΔBAC,
DC = BA  [∵ x = y (Given)]
∠DCA = ∠BAC  [Each 90°]
CA = AC  [Common]
By SAS similarity criterion,
ΔDCA ~ ΔBAC
∴  DA / BC = DC / BA = y / x
⇒  BC / DA = x / y = x / x = 1 / 1
∴  BC : DA = 1 : 1
proved.
iii. ΔCAB ~ ΔCLO
∴  CA / CL = AB / LO  ⇒  z / a = x / d  ⇒  a = (z d) / x
iv. In ΔALO and ΔACD,
We have
∠ALO = ∠ACD = 90°
∠A = ∠A  (common)
∴  By AA similarity criterion,
ΔALO ~ ΔACD
AL / AC = OL / DC
⇒  b / z = d / y
⇒  b = (z d) / y

Q2: Read the source below and answer the questions that follow:

Before Basant Panchami, Samarth is trying to make kites at home. So, he take a rectangular sheet and fold it horizontally, then vertically and fold it transversally. After cutting transversally, he gets a kite shaped figure as shown below: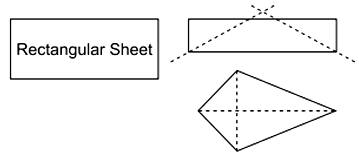

i. What is the angle between diagonals of a rectangle? (1 mark)
ii. Prove that two triangles divided by a diagonal in rectangle are similar as well as congruent. (1 mark)
iii. Prove that the longest diagonal of a kite bisect a pair of opposite angle. (1 mark)
iv. By which similarity criterion the triangles formed by longest diagonal in a kite are similar? (1 mark)

Ans:
i. Diagonals of a rectangle can bisect each other at any angle.
ii. In ΔABC and ΔCDA
AB = CD
∠B = ∠D
BC = DA
ΔABC = ΔCDA
(By SAS)
When two triangles are congruent, then they are similar also.
iii. In ΔAOB and ΔAOD,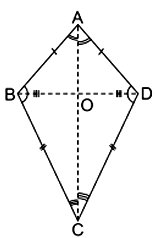

AB = AD
OA = OA  (common)
BO = DO
(Diagonal AC bisect the other diagonal BD)
∴  ΔAOB ~ ΔAOD
(by SSS similarity)
⇒  ∠BAO = ∠DAO  …(1)
In ΔBOC and ΔDOC,
BC = DC
OC = OC  (common)
BO = OD
(Diagonal AC bisect the other diagonal BD)
∴  ΔBOC ~ ΔDOC  (by SSS similarity)
⇒  ∠BCO = ∠DCO  …(2)From (1) and (2), it is clear that, the longest diagonal of a kite bisect a pair of opposite angles.
In ΔABC and ΔADC,
AB = AD
BC = DC
AC = AC  (common)
ΔABC ~ ΔADC
(by SSS criterion)
In ΔABC and ΔADC,
AB = AD
∠ABC = ∠ADC
BC = DC
∴  ΔABC ~ ΔADC     (by SAS criterion)
In ΔABC and ΔADC,
∠B = ∠D
∠BAC = ∠DAC
(∵ ∠BAO = ∠BAC, ∠DAO = ∠DAC, proved above)
∠BCA = ∠DCA
(∵ ∠BCO = ∠BCA, ∠DCO = ∠DCA, proved above)
∴  ΔABC ~ ΔADC     (by AAA similarity)
So, required similarity criterions are SSS, SAS, and AAA.

Q3: Read the source below and answer the questions that follow:

Aman is studying in class X. He observes two towers PQ and RS. The heights of these towers are x m and y m respectively. These towers are z m apart, and O is the point of intersection of the lines joining the top of each tower to the foot of the opposite tower. The distance between point O and M is d. A few questions came to his mind while observing the towers.

i. Which similarity criterion is applicable in ΔPQM and ΔRSM? (1 mark)
ii. If x = y, prove that PQ : RS = 1 : 1. (1 mark)
iii. If QM = a, then find a in terms of x, y, and d. (1 mark)
iv. If PM = b, then find b in terms of x, y, and d. (1 mark)

Ans:
i. In ΔPQM and ΔRSM, we have
∠PQM = ∠RSM = 90°
∠Q = ∠S (common)
.. By AA similarity criterion,
ΔPQM ~ ΔRSM
ii. In ΔPRS and ΔQMP,
RS = PQ [∵ x = y (Given)]
∠PRS = ∠QMP [Each 90°]
PR = RP [Common]
By SAS similarity criterion,
ΔPRS ~ ΔQMP|∴ RS / PQ = y / x
⇒ PQ / RS = x /y = x / x = 1 / 1
∴ PQ : RS = 1 : 1
proved.
iii.  ΔPQM ~ ΔRSM
∴ PQ / QM = RS / MO ⇒ z / a = x / d ⇒ a = (z d) / x
iv. In ΔPMO and ΔPRS,
We have
∠PMO = ∠PRS = 90°
∠P = ∠P (common)
∴ By AA similarity criterion,
ΔPMO ~ ΔPRS
PM / PR = MO / RS
⇒ b / z = d / y
⇒ b = (z d) / y