Case Based Questions: Some Applications to Trignometry - Class 10 PDF Download
Q1: Read the source below and answer the questions that follow:
Kite festival is celebrated in many countries at different times of the year. In India, every year 14th January is celebrated as International Kite Day. On this day many people visit India and participate in the festival by flying various kinds of kites.
The picture given below shows three kites flying together
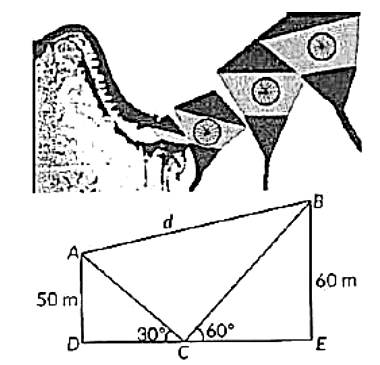 In Fig. the angles of elevation of two kites (Points A and B) from the hands of a man (Point C) are found to be 30° and 60° respectively. Taking AD = 50 m and BE = 60 m, find
In Fig. the angles of elevation of two kites (Points A and B) from the hands of a man (Point C) are found to be 30° and 60° respectively. Taking AD = 50 m and BE = 60 m, find
i. the lengths of strings used (take them straight) for kites A and B as shown in figure. (2 marks)
ii. the distance ‘d' between these two kites. (2 marks)
Ans:
i. Given , AD = 50 m. BE = 60 m
Let the lengths of strings used for kite A be AC and for kite B be BC
Now , in ΔADC, Sin30° = AD/AC
⇒ 1 / 2 = 50 / AC
⇒ AC = 100 m
In ΔBEC,
sin 60° = BE / BC
⇒ √3 / 2 = 60 / BC
⇒ BC = 120 / √3 = 40√3 m.
Hence, AC = 100 m and BC = 40√3 m
ii. Since, the distance between these two kites is d.
ΔABC is a right angle triangle (∵ ∠ACB = 90°)
Now, in ΔABC, by using Pythagoras theorem, we have
BA² = BC² + AC²
⇒ BA² = (40√3)² + (100)²
⇒ BA² = 4800 + 10000 = 14800
⇒ BA = √14800 = 121.65 m
Hence, the distance between these two kites is 121.65 m.
Q2: Read the source below and answer the questions that follow:
Suppose a straight vertical tree is broken at some point due to storm and the broken part is inclined at a certain distance from the foot of the tree.
i. If the top of upper part of broken tree touches ground at a distance of 30 m (from the foot of the tree) and makes an angle of inclination 30°, then find the height of remaining part of the tree. (1 mark)
ii. Find the height of the straight vertical tree. (1 mark)
iii. If the height of a tree is 6 m, which is broken by wind in such a way that its top touches the ground and makes an angle 30° with the ground. Find the length of broken part of the tree. (1 mark)
iv. If AB = 10√√3 m and AD = 2√3 m, then find CD. (1 mark)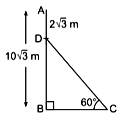
Ans:
i. Let AB be the tree of height h m and let it broken at height of x m, as shown in figure.
Clearly CD = AC = (h - x) m
Now, in right-angled ΔCBD, we have
tan 30° = BC / BD = x / 30
⇒ 1 / √3 = x / 30
⇒ x = 30 / √3= (30 / √3) × (√3 / √3) = (30√3) / 3 = 10√3 m
Thus, the height of remaining part of the tree is 10√3m.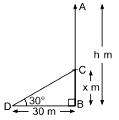
= (30 / √3) × (√3 / √3) = (30√3) / 3 = 10√3 m
Thus, the height of remaining part of the tree is 10√3m.
ii. In right-angled ACBD,
cos 30° = DB / DC = 30 / DC
⇒ √3 / 2 = 30 / DC
⇒ DC = 60 / √3 = (60 / √3) × (√3 / √3) = (60√3) / 3
⇒ DC = 20√3m
from part (1), BC = x = 10√3m
Thus, the height of the straight vertical tree
AB = DC + BC
= 20√3 + 10√3 = 30√3m
iii. Here, h = 6 m and ∠0 = 30°
∴ DC = AC = (6x) m
Now, in right-angled ABCD, we have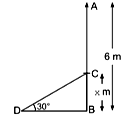 sin 30° = BC / CD⇒ 1 / 2 = x / (6 - x)
sin 30° = BC / CD⇒ 1 / 2 = x / (6 - x)
⇒ 6 - x = 2x
⇒ 3x = 6
⇒ x = 2
So, broken part of tree, AC = 6 - x = 6 - 2 = 4 m.
iv. Clearly, BD = AB - AD
= (10√3 - 2√3) m = 8√3 m
Now, in right-angled ΔBCD, we have
sin 60° = BD / DC
⇒ √3 / 2 = (8√3) / DC
⇒ DC = 16 m
Q3: Read the source below and answer the questions that follow:
Sandeep and his sister Dolly visited at their uncle's place-Birth, Himachal Pradesh. During day time Sandeep, who is standing on the ground spots a paraglider at a distance of 24 m from him at an elevation of 30°. His sister Dolly is also standing on the roof of a 6 m high building, observes the elevation of the same paraglider as 45°. Sandeep and Dolly are on the opposite sides of the paraglider.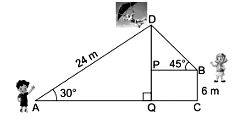
i. Find the distance of paraglider from the ground. (1 mark)
ii. Find the value of PD. (1 mark)
iii. Find the distance between the paraglider and the Dolly. (1 mark)
iv. Find the distance between Sandeep and base of the building. (1 mark)
Ans:
i. In the right-angled ΔAQD, we have
sin 30° = DQ / AD ⇒ 1 / 2 = DQ / 24
⇒ DQ = 12 m
Thus, distance of paraglider from the ground is 12 m.
ii. We have PQ = BC = 6 m
Now, as DQ = 12 m
∴ DP = DQ - PQ = 12 - 6 = 6 m
iii. In right-angled ΔBPD, we have
sin 45° = DP / BD ⇒ 1 / √2 = 6 / BD
⇒ BD = 6√2 m
Thus, the distance of paraglider from the girl is 6√2 m.
iv. In right-angled ΔAQD, we have
cos 30° = AQ / AD
⇒ √3 / 2 = AQ / 24 ⇒ AQ = 12√3 m
In right-angled ΔBPD, we have
cos 45° = BP / BD
⇒ 1 / √2 = BP / 6√2 ⇒ BP = 6m
Thus, the distance between Sandeep and base of the building
= AQ + BP
= 12√3 + 6 = 6(2√3 + 1) m.
Q4: Read the source below and answer the questions that follow:
Radio towers are used for transmitting a range of communication services including radio and television. The tower will either act as an antenna itself or support one or more antennas on its structure. On a similar concept, a radio station tower was built in two Sections A and B. Tower is supported by wires from a point O. Distance between the base of the tower and point O is 36 cm. From point O, the angle of elevation of the top of the Section B is 30° and the angle of elevation of the top of Section A is 45°.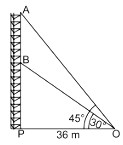
i. Find the length of the wire from the point O to the top of Section B. (1 mark)
ii. Find the height of the Section A from the base of the tower. (1 mark)
iii. Find the distance AB. (1 mark)
iv. Find the area of AOPB. (1 mark)
Ans: i. Let the length of the wire from the point O to the top of section B, i.e., OB = l m.
i. Let the length of the wire from the point O to the top of section B, i.e., OB = l m.
Given, OP = 36 cm and ∠BOP = 30°
Now in right-angled ΔBPO,
cos 30° = OP / OB
⇒ √3 / 2 = 36 / l
⇒ l = (72 / √3) × (√3 / √3) = (72√3) / 3 = 24√3
So, required length is 24√3 cm.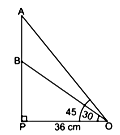 ii. Given, ∠AOP = 45° and OP = 36 cm
ii. Given, ∠AOP = 45° and OP = 36 cm
Now in right-angled ΔAPO,
tan 45° = AP / OP
⇒ 1 = AP / 36
⇒ AP = 36 cm
∴ The height of the Section A from the base of the tower = AP = 36 cm.
iii. Now, in right-angled ΔBPO,
tan 30° = BP / OP
⇒ 1 / √3 = BP / 36
⇒ BP = (36 / √3) × (√3 / √3) = (36√3) / 3 = 12√3 cm
∴ AB = AP - BP (∵ AP = 36 cm)
= 36 - 12√3 = 12(3 - √3) cm
So, required distance AB is 12(3 - √3) cm.
iv. Since, ΔBPO is a right-angled triangle.
∴ Area of ΔOPB = (1 / 2) × base × height
= (1 / 2) × OP × BP
= (1 / 2) × 36 × 12√3
= 216√3 cm².
Q5: Read the source below and answer the questions that follow:
A boy is standing on the top of light house. He observed that boat P and boat Q are approaching the light house from opposite directions. He finds that angle of depression of boat P is 45° and angle of depression of boat Q is 30°. He also knows that height of the light house is 100 m.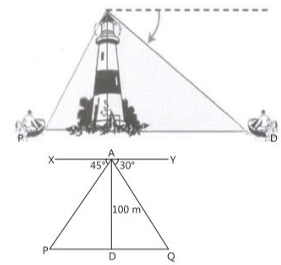
i. What is the measure of APD? (1 mark)
ii. If ZYAQ = 30°, then ZAQD is also 30°, why? (1 mark)
iii. Find length of PD. (1 mark)
iv. Find length of QD. (1mark)
Ans: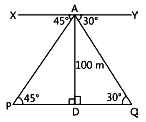
i. Let a boy is standing on the top (A) of light house (AD).
Here XYII PQ and AP is traversal.
∴ ∠APD = ∠PAX (Alternative interior angles)
⇒ ∠APD = 45°.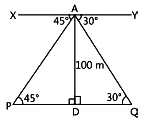 ii. Given, ∠YAQ = 30°
ii. Given, ∠YAQ = 30°
⇒ ∠AQD = 30°
Because, XYIIPQ and AQ is a traversal.
So, alternate interior angles are equal.
∴ ∠YAQ = ∠AQD.
iii. In right-angled ΔADP,
tan 45° = AD / PD
⇒ 1 = 100 / PD
⇒ PD = 100 m.
∴ Boat P is 100 m from the light house.
iv. In right-angled ΔADQ,
tan 30° = AD / DQ
⇒ 1 / √3 = 100 / DQ
⇒ QD = 100√3 m
∴ Boat Q is 100√3 m from the light house.
FAQs on Case Based Questions: Some Applications to Trignometry - Class 10
| 1. What are some real-life applications of trigonometry? |  |
| 2. How does the sine function relate to right triangles? |  |
| 3. What is the significance of the unit circle in trigonometry? |  |
| 4. How can trigonometric identities be used to simplify expressions? |  |
| 5. What is the relationship between the angles of elevation and depression and trigonometric functions? |  |














