Case Based Question: Areas Related to Circles | Mathematics (Maths) Class 10 PDF Download
Q1: Read the source below and answer the questions that follow:
A stable owner has four horses. He usually ties these horses with 7 m long rope to pegs at each corner of a square-shaped grass field of 20 m length, to graze in his farm. But tying with rope sometimes results in injuries to his horses, so he decided to build a fence around the area so that each horse could graze.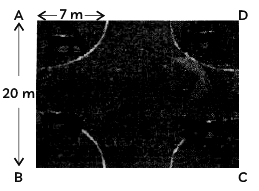
i. Find the area of the square-shaped grass field. (1 mark)
ii. Find the area of the total field in which these horses can graze. (1 mark)
iii. If the length of the rope of each horse is increased from 7 m to 10 m, find the area grazed by one horse. (Use π = 3.14) (1 mark)
iv. What is the area of the field that is left ungrazed, if the length of the rope of each horse is 7 m? (1 mark)
Ans:
i. Area of square shaped field
= 20 × 20
= 400 sq. m.
ii. Area of 4 quadrants
= Area of a circle of radius 7 m = πr²
= (1 / 4) × (22 / 7) × 7 × 7
= 154 m²
iii. New radius = 10 m
So, area grazed by one horse
= (1 / 4) × (Area of circle with radius 10 m)
= (1 / 4) × π × (10)²
= (3.14 × 10 × 10) / 4
= 78.5 m²
iv. Area of ungrazed portion
= Area of square field - Area of circle with radius 7 m
= 20 × 20 - (22 / 7) × 7 × 7
= 400 - 154
= 246 m²
Q2: Read the source below and answer the questions that follow:
Flower beds look beautiful growing in gardens. One such circular park of radius 'r' m, has two segments with flowers. One segment which subtends an angle of 90° at the centre is full of red roses, while the other segment with central angle 60° is full of yellow coloured flowers.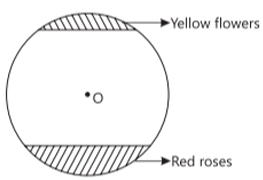 It is given that the combined area of the two segments (of flowers) is 256 (2/3) sq. m.
It is given that the combined area of the two segments (of flowers) is 256 (2/3) sq. m.i. Write an equation representing the total area of the two segments in terms of 'r'. (1 mark)
ii. Find the value of 'r'. (1 mark)
iii. Find the area of the segment with red roses. (1 mark)
iv. Find the area of the segment with yellow flowers. (1 mark)
Ans:
i. Given, radius of circular park = r m.
Central angle for segment of red roses (O1) = 90°
Central angle for segment of yellow roses (O2) = 60°
Now, area of segment of yellow roses
= [(θ₂π / 180°) - sinθ₂] × (r² / 2)
= [(60°π / 180°) - sin60°] × (r² / 2)
= [(π / 3) - sin60°] × (r² / 2)
= [(π / 3) - (√3 / 2)] × (r² / 2)
= r² [(π / 3) - (√3 / 2)] m²
and area of segment of red roses
= [(θ₁π / 180°) - sinθ₁] × (r² / 2)
= [(90°π / 180°) - sin90°] × (r² / 2)
= [(π / 2) - sin90°] × (r² / 2)
= [(π / 2) - 1] × (r² / 2) m²
Given, total area of the two segments = 256 (2/3) m²
⇒ Area of segment of (red roses + yellow roses)
= 770 / 3 m²
∴ (r² / 2) [(π / 2) - 1] + (r² / 2) [(π / 3) - (√3 / 2)] = 770 / 3 ...(i)
ii. From eq (i),
(r² / 2) [(π / 2) - 1 + (π / 3) - (√3 / 2)] = 770 / 3
⇒ (r² / 2) [(5π / 6) - 1.732] = 770 / 3
⇒ (r² / 2) [(5 / 6 × 22 / 7) - 1 - 0.866] = 770 / 3
⇒ (r² / 2) [2.619 - 1.866] = 770 / 3
⇒ (r² / 2) × 0.753 = 770 / 3
⇒ r² = (770 × 2) / (0.753 × 3)
⇒ r² = 1540 / 2.259
⇒ r² = 681.72
⇒ r = 26.1 m
iii. The area of segment with red roses
= (r² / 2) [(π / 2) - 1]
= (681.72 / 2) [(22 / 2 × 7) - 1]
= 340.86 × 0.57
= 194.3 m²
The area of segment with yellow roses
= (r² / 2) [(π / 3) - (√3 / 2)]
= (681.72 / 2) [(22 / 3 × 7) - (1.732 / 2)]
= 340.86 × (1.0476 - 0.866)
= 340.86 × 0.1816
= 61.9 m²
Q3: Read the source below and answer the questions that follow:
Interschool Rangoli Competition was organized by one of the reputed schools of odissa. The theme of the Rangoli Competition was Diwali celebrations where students were supposed to make mathematical designs. Students from various schools participated and made beautiful Rangoli designs. One such design is given below.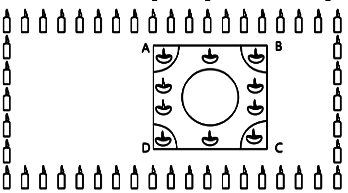 Rangoli is in the shape of square marked as ABCD, side of square being 40 cm. At each corner of a square, a quadrant of circle of radius 10 cm is drawn (in which diyas are kept). Also a circle of diameter 20 cm is drawn inside the square.
Rangoli is in the shape of square marked as ABCD, side of square being 40 cm. At each corner of a square, a quadrant of circle of radius 10 cm is drawn (in which diyas are kept). Also a circle of diameter 20 cm is drawn inside the square.i. What is the area of square ABCD? (1 mark)
ii. Find the area of the circle. (1 mark)
iii. If the circle and the four quadrants are cut off from the square ABCD and removed, then find the area of remaining portion of square ABCD. (1 mark)
iv. Find the combined area of 4 quadrants and the circle, removed. (1 mark)
Ans:
i. Given, side of square ABCD, 'a' = 40 cm.
∴ Area of square ABCD = a² = (40)²
= 1600 cm².
ii. Given, diameter of inside circle = 20 cm
∴ Radius of circle (r) = 20 / 2 = 10 cm
So, area of the circle = πr²
= π(10)² = 100π
= 100 × 3.14 = 314 cm²
iii. Given, radius of a quadrant (R) = 10 cm
All quadrants are equal at each corner of a square ABCD.
Now, area of a quadrant = (1/4) πR²
= (1/4) π(10)²
= (1/4) × π × 100 = 25π cm²
∴ Area of four quadrants = 4 × 25π = 100π
= 100 × 3.14 = 314 cm²
So, area of remaining portion of square ABCD
= Area of square ABCD - Area of the circle - Area of four quadrants
= 1600 - 314 - 314
= 1600 - 628 = 972 cm²
iv. Combined area of 4 quadrants and the circle, removed
= Area of four quadrants + Area of the circle
= 314 + 314
= 628 cm²
Q4: Read the source below and answer the questions that follow:
Kritika bought a pendulum clock for her living room. The clock contains a small pendulum of length 15 cm. The minute hand and hour hand of the clock are 9 cm and 6 cm long respectively.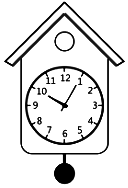
i. Find the area swept by the minute hand in 10 minutes. (1 mark)
ii. If the pendulum covers a distance of 22 cm in the complete oscillation, then find the angles described by pendulum at the centre.
(1 mark)
iii. Find the area swept by the hour hand in 1 hour. (1 mark)
iv. Find the area swept by the hour hand between 11 am and 5 pm (1 mark)
Ans:
i. Area swept by the minute hand in 10 minutes:
Given, length of minute hand = 9 cm
The minute hand completes 360° in 60 minutes.
Angle swept by the minute hand in 10 minutes:
(10/60) × 360° = 60°
Area swept by the minute hand = (θ / 360) × πr²
(60/360) × 3.14 × (9)²
(1/6) × 3.14 × 81
254.34 / 6
42.39 cm²
ii. Angle described by the pendulum at the centre:
Given, Length of the pendulum (r) = 15 cm
Distance covered by the pendulum in one complete oscillation = 22 cm
Angle described at the centre:
θ = (arc length / radius) × (180° / π)
= (22 / 15) × (180 / 3.14)
= 3960 / 47.1
≈ 84°
iii. Area swept by the hour hand in 1 hour:
Given, length of hour hand = 6 cm
The hour hand completes 360° in 12 hours.
Angle swept by the hour hand in 1 hour:
(1/12) × 360° = 30°
Area swept by the hour hand in 1 hour = (θ / 360) × πr²
(30/360) × 3.14 × (6)²
= (1/12) × 3.14 × 36
= 113.04 / 12
= 9.42 cm²
iv. Area swept by the hour hand between 11 am and 5 pm:
Time duration = 5 hours
Angle swept by the hour hand:
5 × 30° = 150°
Area swept:
= (150/360) × π × (6)²
= (5/12) × 3.14 × 36
= 565.2 / 12
= 47.1 cm²
Thus, the area swept by the hour hand between 11 am and 5 pm is 47.1 cm².
|
127 videos|584 docs|79 tests
|
FAQs on Case Based Question: Areas Related to Circles - Mathematics (Maths) Class 10
| 1. What is the formula for calculating the area of a circle? |  |
| 2. How do you find the circumference of a circle? |  |
| 3. What is the relationship between the radius and diameter of a circle? |  |
| 4. How do you convert the area of a circle to different units? |  |
| 5. What are some real-life applications of circle area calculations? |  |
















