Case Based Questions: Surface Areas and Volumes | Mathematics (Maths) Class 10 PDF Download

Q1: Read the source below and answer the questions that follow:

i. How many square cm paper would be used to make 4 such caps? (2 marks)
ii. The bakery shop sells cakes by weight (0.5 kg, 1 kg, 1.5 kg. etc..}. To have the required dimensions how much cake should they order if 650 cm3 equals 100 g of cake? (2 marks)

Ans:
i. Paper required to make four caps:
Given, base circumference of cone = 44 cm
Height of the cone = 24 cm
Radius of the cone:
r = c / (2π) = 44 / (2 × 22/7) = 7 cm
Curved Surface Area (CSA) of the cone:
CSA = πr√(h² + r²)
(22/7) × 7 × √(24² + 7²)
22 × √625
22 × 25
550 cm²
Paper required for one cap = 550 cm²
For four caps:
550 × 4 = 2,200 cm²
ii. Weight of the cylindrical shape cake:
Given, diameter of the cake = 24 cm
Height of the cake = 14 cm
Radius of the cake:
r = d / 2 = 24 / 2 = 12 cm
Volume of the cylinder:
V = πr²h
= (22/7) × (12)² × 14
= (22/7) × 144 × 14
= 6,336 cm³
Given, 650 cm³ of cake = 100 g of cake
Required weight:
(6,336 / 650) × 100
= 974.76 g ≈ 1 kg
Bakery shop sells cakes in 0.5 kg, 1 kg, and 1.5 kg packs.
Since 974.76 g ≈ 1 kg, a **1 kg cake** should be ordered.
Thus, the required weight of the cylindrical shape cake is 1 kg.

Q2: Read the source below and answer the questions that follow:

i. What is the area of the canvas used in making the tent? (2 marks)
ii. What is the total area of the canvas bought for the tent? (1 marks)
iii. What is the total cost of the canvas required for the tent? (1 marks)

Ans:
According to given information, we have the following figure.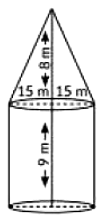
i. Area of the canvas used in making the tent:
Given, radius of conical and cylindrical part = 15 m
Height of the conical part (h) = 8 m
Height of the cylindrical part (H) = 9 m
Slant height (l) of conical part:
l = √(r² + h²)
= √(15² + 8²)
= √(225 + 64)
= √289
= 17 m
Curved Surface Area (CSA) of the tent:
CSA = πr(l + 2H)
= (22/7) × 15 × (17 + 2 × 9)
= (22/7) × 15 × 35
= 1650 m²
ii. Total area of the canvas bought:
Extra canvas added = 30 m²
Total area:
1650 + 30 = **1680 m²
iii. Total cost of the canvas:
Cost per square meter = ₹ 200
Total cost:
1680 × 200 = ₹ 3,36,000
Thus, the total cost of the canvas required for the tent is ₹ 3,36,000

Q3: Read the source below and answer the questions that follow:

i. Find the volume of wood carved out to make one cylindrical hollow. (1 mark)
ii. Find the lateral surface area of the cuboid to paint it with green colour. (1 mark)
iii. Find the volume of wood in the remaining cuboid after carving out seven cylindrical hollows. (1 mark)
iv. Find the surface area of the top surface of the cuboid to be painted yellow. (1 mark)

Ans:
i. Given, height of the hollow cylinder (h) = 3 cm
and radius of the hollow cylinder (r) = 2 cm
So, the volume of wood carved out to make one cylindrical hollow
= volume of a hollow cylinder
= πr²h
= (22/7) × (2²) × 3 = (22/7) × 12 = 264/7 cm³
ii. Given, length of the cuboidal wooden block (l) = 14 cm,
breadth of the cuboidal wooden block (b) = 17 cm
and height of the cuboidal wooden block (h) = 4 cm
:- Lateral surface area of the cuboid to paint it with green colour
= 2 (l + b) × h
= 2 (14+17) × 4
= 2 × 31 × 4 = 248 cm²
iii. Volume of cuboidal wooden block = l × b × h
= 14 × 17 × 4
= 952 cm²
and volume of seven cylindrical hollows
= 7 × volume of a hollow cylinder
= 7 × (264/7) = 264 cm³
:- The volume of wood in the remaining cuboid after carving out seven cylindrical hollows.
= volume of cuboidal block - volume of seven cylindrical hollows.
= 952 - 264 = 688 cm³
iv. Surface area of the top surface of the cuboid
= l × b = 14 × 17 = 238 cm²
and curved surface area of seven circular region
= 7 × πr² = 7 × (22/7) × 2² × 4 = 88 cm²
:- The surface area of the top surface of the cuboid to be painted yellow surface area of the top surface of the cuboid - C.S.A of seven circular region
= 238 - 88 = 150 cm².

Q4: Read the source below and answer the questions that follow:

i. Find the area of the base of the cylindrical cup. (1 mark)
ii. What is the curved surface area of the cylindrical cup? (1 mark)
iii. What is the capacity of the hemispherical cup? (1 mark)
iv. Find the capacity of the cylindrical cup. (1 mark)

Ans:
i. Let r and h be the radius and height of the cylindrical cup respectively.
Given, diameter of the base = 7 cm
∴ Its radius (r) = 7/2 cm
So, base area of the cylindrical cup = πr²
= (22/7) × (7/2)²
= (22/7) × (49/4)
= 77/2
= 38.5 cm².
ii. In cylindrical cup.
Given, radius (r) = 7/2 cm and height (h) = 14 cm
∴ Curved surface area of the cylindrical cup
= 2πrh
= 2 × (22/7) × (7/2) × 14
= 308 cm².
iii. Let R be the radius of the hemispherical cup.
Given, diameter of hemispherical cup = 21 cm
Its radius (R) = 21/2 cm
So, capacity of the hemispherical cup
= (2/3) πR³
= (2/3) × (22/7) × (21/2)³
= (11 × 21 × 21)/2
= 2425.5 cm³.
iv. Given, height of the cylindrical cup (h) = 14 cm
and its radius (r) = 7/2 cm
Capacity of the cylindrical cup
= πr²h
= (22/7) × (7/2)² × 14
= 11 × 7 × 7
= 539 cm³.