डेटा प्रतिनिधित्व | SSC CGL Tier 2 - Study Material, Online Tests, Previous Year (Hindi) PDF Download

डेटा प्रतिनिधित्व उस विधि को संदर्भित करता है जिसका उपयोग कंप्यूटर में संग्रहीत जानकारी को आंतरिक रूप से प्रदर्शित करने के लिए किया जाता है। कंप्यूटर विभिन्न प्रकार की जानकारी जैसे संख्याएँ, पाठ, ग्राफ़िक्स, और ध्वनियाँ संग्रहीत करते हैं।

संख्यात्मक प्रणाली

• संख्यात्मक प्रणाली एक तकनीक है जिसका उपयोग कंप्यूटर की आर्किटेक्चर में संख्याओं का प्रतिनिधित्व करने के लिए किया जाता है। कंप्यूटर मेमोरी में सहेजी गई या पुनः प्राप्त की गई हर मान एक विशिष्ट संख्यात्मक प्रणाली का पालन करती है।

संख्यात्मक प्रणालियों के प्रकार

• द्विआधारी संख्यात्मक प्रणाली: इसे बेस 2 प्रणाली के रूप में जाना जाता है, यह कंप्यूटरों के लिए अत्यधिक प्रभावी है लेकिन मनुष्यों के लिए नहीं। इसमें केवल दो अनूठे अंक होते हैं, 0 और 1। एक स्ट्रिंग जिसमें इन दोनों अंकों का कोई भी संयोजन होता है (जहाँ प्रत्येक अंक को बिट कहा जाता है) उसे द्विआधारी संख्या कहा जाता है। कंप्यूटर इनपुट की गणना द्विआधारी रूप में करते हैं, और डिजिटल कंप्यूटर आंतरिक रूप से डेटा का प्रतिनिधित्व करने और अंकगणितीय गणनाएँ करने के लिए द्विआधारी संख्यात्मक प्रणाली का उपयोग करते हैं। उदाहरण के लिए, (10101)₂, जहाँ 2 द्विआधारी संख्या का आधार दर्शाता है।
• दशमलव संख्यात्मक प्रणाली: यह वह प्रणाली है जिसका हम अपने दैनिक जीवन में उपयोग करते हैं। इसमें 10 अंक होते हैं, 0 से 9, जो किसी भी संख्यात्मक मान का प्रतिनिधित्व कर सकते हैं। इसे बेस 10 प्रणाली या स्थितिगत संख्यात्मक प्रणाली के रूप में भी जाना जाता है। उदाहरण के लिए, (1275)₁₀, जहाँ 10 दशमलव संख्या का आधार दर्शाता है।
• अक्टल संख्यात्मक प्रणाली: इस प्रणाली में 8 अंक होते हैं, 0 से 7, और इसे बेस 8 प्रणाली के रूप में जाना जाता है। एक अक्टल संख्या की प्रत्येक स्थिति आठ की क्रमिक शक्ति का प्रतिनिधित्व करती है। उदाहरण के लिए, (234)₈, जहाँ 8 अक्टल संख्या का आधार दर्शाता है।
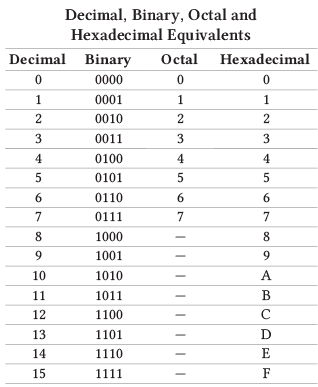
• हेक्साडेसिमल संख्यात्मक प्रणाली: यह प्रणाली द्विआधारी संख्याओं के साथ काम करने के लिए एक संक्षिप्त विधि प्रदान करती है। इसमें 16 अनूठे अंक होते हैं: 0 से 9 और A से F, जहाँ A 10 को, B 11 को, और इसी तरह F 15 को दर्शाता है। इसे बेस 16 प्रणाली या बस हेक्स के रूप में भी जाना जाता है। एक हेक्साडेसिमल संख्या की प्रत्येक स्थिति 16 की क्रमिक शक्ति का प्रतिनिधित्व करती है।

उदाहरण के लिए, (F9D)₁₆ यहाँ, 16 हेक्साडेसिमल संख्या का आधार दर्शाता है।

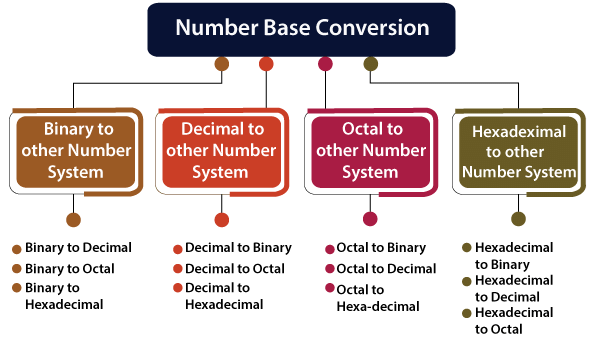
संख्यात्मक प्रणाली के बीच रूपांतरण

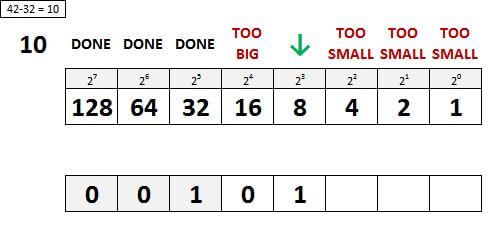
दशमलव संख्या को द्विआधारी (Binary) में रूपांतरित करने के लिए निम्नलिखित चरणों का पालन करें:

• दिये गए संख्या को 2 से विभाजित करें।
• भागफल और शेषफल को नोट करें। शेषफल 0 या 1 होना चाहिए।
• यदि भागफल 0 नहीं है, तो भागफल को फिर से 2 से विभाजित करें और चरण 2 को दोहराएं।
• यदि भागफल 0 है, तो प्रक्रिया को रोक दें।
• पहला शेषफल को Least Significant Bit (LSB) कहा जाता है, और अंतिम शेषफल को Most Significant Bit (MSB) कहा जाता है।
• सभी शेषफलों को MSB से LSB तक व्यवस्थित करें ताकि द्विआधारी संख्या बने।

द्विआधारी से दशमलव

द्विआधारी संख्या को दशमलव में रूपांतरित करने के लिए निम्नलिखित चरणों का पालन करें:

• प्रत्येक द्विआधारी अंक को 2 की संबंधित शक्ति से गुणा करें।
• पूर्णांक भाग के लिए, सकारात्मक शक्तियों का उपयोग करें, और अंश भाग के लिए, नकारात्मक शक्तियों का उपयोग करें।
• सभी परिणामस्वरूप मानों को जोड़ें ताकि दशमलव समकक्ष प्राप्त हो।

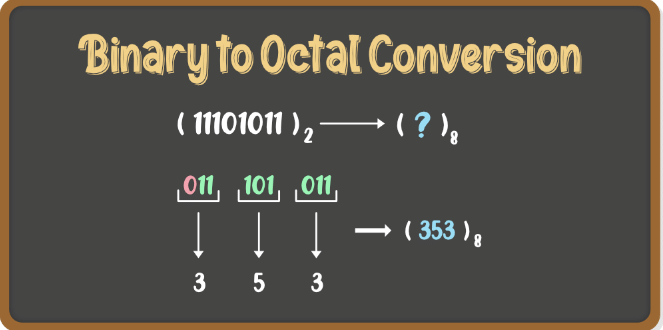
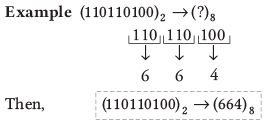
द्विआधारी से अष्टाधारी (Octal)

द्विआधारी को अष्टाधारी में रूपांतरित करने के लिए निम्नलिखित चरणों का पालन करें:

• चरण 1: दाएं से बाएं 3 बिट्स का समूह बनाएं। यदि बाईं ओर का समूह 3 बिट्स से कम है, तो बाईं ओर आवश्यक संख्या में अग्रणी 0 डालें।
• चरण 2: अब, प्रत्येक समूह को दशमलव संख्या में रूपांतरित करें।

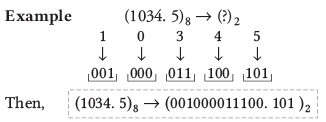
अष्टाधारी से द्विआधारी

संख्याओं के प्रत्येक अंक को अष्टाधारी से द्विआधारी में 3 बिट्स के समूह में रूपांतरित करें।

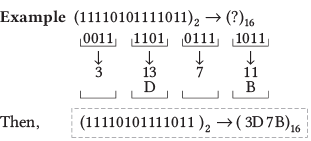
द्विआधारी से हेक्साडेसिमल

द्विआधारी संख्या को उसके हेक्साडेसिमल समकक्ष में रूपांतरित करने के लिए निम्नलिखित चरणों का पालन करें:

• द्विआधारी अंकों को 4 बिट्स के सेट में समूहित करें, दाएं से शुरू करते हुए। यदि बाईं ओर का समूह 4 बिट्स से कम है, तो बाईं ओर आवश्यक संख्या में अग्रणी 0 जोड़ें।
• 4 बिट्स के प्रत्येक समूह को उसके दशमलव समकक्ष में रूपांतरित करें।

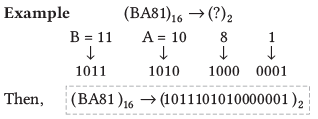
हेक्साडेसिमल से द्विआधारी

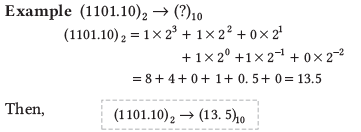
हेक्साडेसिमल से बाइनरी

इस प्रकार के रूपांतरण के लिए, प्रत्येक हेक्साडेसिमल अंक को 4 बिट बाइनरी समकक्ष में परिवर्तित करें।

दशमलव से ऑक्टल

एक दशमलव संख्या को उसके ऑक्टल समकक्ष में परिवर्तित करने के लिए, निम्नलिखित चरणों का पालन करें:

• दी गई संख्या को 8 से विभाजित करें।
• उपज और शेष को रिकॉर्ड करें। शेष 0 से 7 के बीच का अंक होगा।
• यदि उपज 0 नहीं है, तो उपज को फिर से 8 से विभाजित करें और चरण 2 दोहराएं।
• यदि उपज 0 है या 8 से कम है, तो प्रक्रिया रोक दें।
• हर शेष को बाईं से दाईं ओर लिखें, सबसे महत्वपूर्ण अंक (MSD) से लेकर सबसे कम महत्वपूर्ण अंक (LSD) तक।

ऑक्टल से दशमलव

ऑक्टल से दशमलव

ऑक्टल को दशमलव में परिवर्तित करने के लिए, निम्नलिखित चरणों का पालन करें:

• प्रत्येक ऑक्टल संख्या के अंकों को 8 की शक्तियों से गुणा करें।
• ये शक्तियाँ पूर्णांक भाग के लिए सकारात्मक और अंश भाग के लिए नकारात्मक होनी चाहिए।
• सभी गुणा किए गए अंकों को जोड़ें।

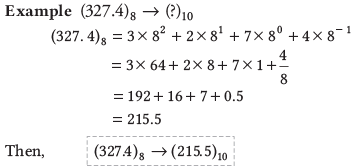
दशमलव से हेक्साडेसिमल

दशमलव से हेक्साडेसिमल

एक दशमलव संख्या को उसके हेक्साडेसिमल समकक्ष में परिवर्तित करने के लिए, निम्नलिखित चरणों का पालन करें:

• दी गई संख्या को 16 से विभाजित करें।
• उपज और शेष को रिकॉर्ड करें। शेष 0 से 9 के बीच का अंक या A से F के बीच का एक अक्षर होगा।
• यदि उपज 0 नहीं है, तो उपज को फिर से 16 से विभाजित करें और चरण 2 दोहराएं।
• यदि उपज 0 है या 16 से कम है, तो प्रक्रिया रोक दें।
• हर शेष को बाईं से दाईं ओर लिखें, सबसे महत्वपूर्ण अंक (MSD) से लेकर सबसे कम महत्वपूर्ण अंक (LSD) तक।

हेक्साडेसिमल से दशमलव

हेक्साडेसिमल से डेसिमल

हेक्साडेसिमल को डेसिमल में परिवर्तित करने के लिए निम्नलिखित चरण शामिल हैं:

• चरण 1: हेक्साडेसिमल संख्या के प्रत्येक अंक को 16 की शक्ति से गुणा करें।
• चरण 2: ये शक्तियाँ पूर्णांक भाग के लिए सकारात्मक और अंश भाग के लिए नकारात्मक होनी चाहिए।
• चरण 3: सभी गुणा किए गए अंकों को जोड़ें।

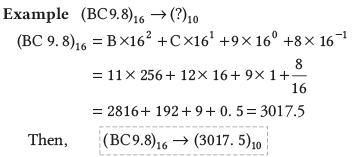
ऑक्टल से हेक्साडेसिमल

ऑक्टल से हेक्साडेसिमल

ऑक्टल को हेक्साडेसिमल में परिवर्तित करने के लिए निम्नलिखित चरण शामिल हैं:

• चरण 1: ऑक्टल संख्या के प्रत्येक अंक को बाइनरी संख्या में परिवर्तित करें।
• चरण 2: फिर, प्रत्येक बाइनरी अंक को हेक्साडेसिमल संख्या में परिवर्तित करें।

हेक्साडेसिमल से ऑक्टल

हेक्साडेसिमल से ऑक्टल

हेक्साडेसिमल को ऑक्टल में परिवर्तित करने के लिए निम्नलिखित चरण शामिल हैं:

• चरण 1: हेक्साडेसिमल संख्या के प्रत्येक अंक को बाइनरी संख्या में परिवर्तित करें।
• चरण 2: फिर, प्रत्येक बाइनरी अंक को ऑक्टल संख्या में परिवर्तित करें।

कंप्यूटर कोड

• कंप्यूटर में, कोई भी चरित्र, जैसे कि एक वर्ण, अंक, या विशेष चरित्र, 1 और 0 के एक अद्वितीय कोडित पैटर्न द्वारा दर्शाया जाता है।
• ये कोड निश्चित आकार के बाइनरी स्थितियों के समूहों से बने होते हैं।
• सबसे सामान्य रूप से उपयोग किए जाने वाले बाइनरी कोडिंग योजनाएँ हैं:

बाइनरी कोडेड डेसिमल (BCD)

• IBM द्वारा विकसित, BCD एक प्रणाली है जिसमें प्रत्येक दशमलव अंक का प्रतिनिधित्व करने के लिए चार बिट्स का उपयोग किया जाता है।
• यह बाइनरी अंकों का उपयोग करके दशमलव अंकों (0-9) का प्रतिनिधित्व करता है और संख्या के आकार पर कोई सीमा नहीं है।

अमेरिकन स्टैंडर्ड कोड फॉर इंफॉर्मेशन इंटरचेंज (ASCII)

ASCII एक मानक चरित्र कोड है जिसका उपयोग डेटा को स्टोर करने के लिए किया जाता है ताकि इसे अन्य सॉफ़्टवेयर कार्यक्रमों द्वारा उपयोग किया जा सके। ASCII कोड के दो प्रकार होते हैं:

• ASCII-7: एक 7-बिट मानक ASCII कोड है जो 27 = 128 अद्वितीय प्रतीकों या वर्णों (0 से 127 तक) की अनुमति देता है।
• ASCII-8: ASCII-7 का एक विस्तारित संस्करण। यह एक 8-बिट कोड है जो 28 = 256 अद्वितीय प्रतीकों या वर्णों (0 से 255 तक) की अनुमति देता है।

Extended Binary Coded Decimal Interchange (EBCDIC)

ईबीसीडीआईसी में, वर्णों का प्रतिनिधित्व आठ बिट्स द्वारा किया जाता है। यह कोड 2^8 = 256 अद्वितीय बिट्स के संयोजनों की अनुमति देता है और जानकारी को अन्य कंप्यूटरों द्वारा पढ़ने योग्य रूप में संग्रहित करता है।

लॉजिक गेट

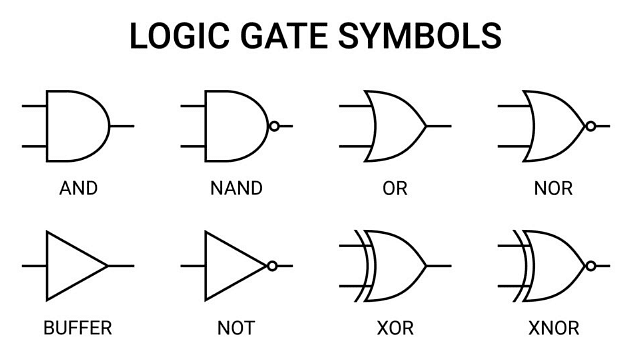
एक लॉजिक गेट एक डिजिटल सर्किट का एक बुनियादी निर्माण खंड है जिसमें दो इनपुट और एक आउटपुट होता है। इनपुट और आउटपुट के बीच का संबंध एक विशेष लॉजिक पर आधारित होता है। इन गेट्स को ट्रांजिस्टर और डायोड जैसे इलेक्ट्रॉनिक स्विच का उपयोग करके लागू किया जाता है।

लॉजिक गेट के विभिन्न प्रकार निम्नलिखित हैं:

1. AND गेट: इस गेट को (⋅) द्वारा भी दर्शाया जाता है, अर्थात् (A ⋅ B)। यह केवल तभी True लौटाता है जब दोनों शर्तें या इनपुट True हों, अन्यथा यह False लौटाता है।

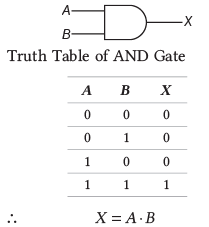
2. OR गेट: इसे ( ) द्वारा दर्शाया जाता है, अर्थात् (A B)। यह True लौटाता है यदि किसी एक शर्त या इनपुट का मान True है और यदि दोनों शर्तें False हैं, तो यह False लौटाता है।

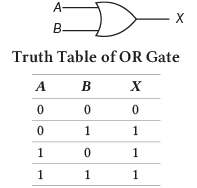
∴ X = A B

3. इन्वर्टर या NOT गेट: इस गेट को (′) द्वारा दर्शाया जाता है, अर्थात् A ′। यह तब True लौटाता है जब इनपुट False हो और इसके विपरीत।

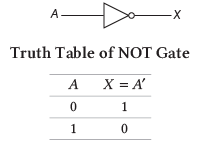
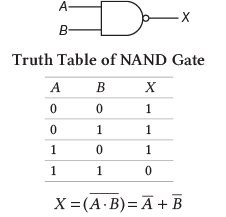
4. NAND गेट: यह मूलतः AND गेट का उलटा है। इस गेट को AND और NOT गेट को मिलाकर डिज़ाइन किया गया है।

यह केवल तभी False लौटाता है जब दोनों शर्तें या इनपुट True हों, अन्यथा यह True लौटाता है।

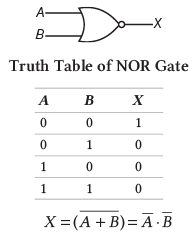
5. NOR गेट: यह OR गेट का विपरीत है। इस गेट को OR और NOT गेट को मिलाकर डिज़ाइन किया गया है। यह तब ही True लौटाता है जब दोनों शर्तें या इनपुट False होते हैं, अन्यथा यह False लौटाता है।

नोट: NAND और NOR गेट्स को भी यूनिवर्सल गेट्स कहा जाता है।

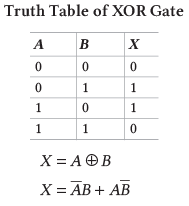
6. एक्सक्लूसिव-OR या XOR गेट: यह OR गेट के संचालन के आधार पर कार्य करता है। यह तब ही True लौटाता है जब दोनों शर्तों में से एक शर्त सही हो, अन्यथा यह False लौटाता है।

टिप्स:

• Unicode डेटा में प्रतीकों का प्रतिनिधित्व करने के लिए 16 बिट्स का उपयोग करता है, जिसमें गैर-अंग्रेजी वर्ण और विभिन्न भाषाओं जैसे चीनी और जापानी के वैज्ञानिक प्रतीक शामिल हैं।
• किसी बाइनरी संख्या का वन'स कंप्लीमेंट उस मान को संदर्भित करता है जो सभी बिट्स को पलटने पर प्राप्त होता है। उदाहरण के लिए, 110100 को पलटने पर 001011 प्राप्त होता है।