परिचय: संख्या प्रणाली - RRB NTPC/ASM/CA/TA PDF Download

संख्याएँ हमारे जीवन का एक महत्वपूर्ण हिस्सा हैं। इस अध्याय में, हम संख्याओं के विभिन्न प्रकारों और उनके अंतर्गत आने वाली विभिन्न श्रेणियों के बारे में जानेंगे। यहाँ पर चर्चा की गई अवधारणाएँ आपके लिए MBA प्रवेश परीक्षाओं को पास करने के लिए गणितीय आवश्यकताओं को समझने की ओर पहला कदम होंगी। जैसे-जैसे हम इस अध्याय में आगे बढ़ेंगे, आप महसूस करेंगे कि आपने पहले से ही स्कूल में कई अवधारणाएँ सीख ली हैं। इससे आपके आत्मविश्वास को और बढ़ावा मिलेगा।

संख्या क्या है?

एक संख्या एक गणितीय अवधारणा है जिसका उपयोग चीजों की गिनती, मापने या लेबल करने के लिए किया जाता है। संख्याएँ अंकगणितीय गणनाओं में एक महत्वपूर्ण भूमिका निभाती हैं।

• इनके विभिन्न प्रकार होते हैं, जिनमें प्राकृतिक संख्याएँ, पूर्ण संख्याएँ, तार्किक संख्याएँ और अतार्किक संख्याएँ शामिल हैं।
• यहाँ तक कि 0 भी एक संख्या है, जो शून्य मान का प्रतिनिधित्व करती है।
• संख्याओं को 2 द्वारा विभाज्यता के आधार पर सम या विषम के रूप में वर्गीकृत किया जा सकता है, और प्राइम या संयोजित के रूप में उनके गुणकों की संख्या के आधार पर।
• सम और विषम का अर्थ 2 द्वारा विभाज्यता है, जबकि प्राइम संख्याएँ केवल दो गुणकों वाली होती हैं, और संयोजित संख्याएँ दो से अधिक होती हैं।
• संख्या प्रणालियों में, ये संख्याएँ अंक के रूप में कार्य करती हैं। बाइनरी प्रणाली में सामान्य अंकों के रूप में 0 और 1 का उपयोग किया जाता है, जबकि अन्य प्रणालियाँ 0 से 9 तक के अंकों का उपयोग करती हैं।
• विभिन्न प्रकार की संख्याओं और उनके प्रणालियों को समझना गणित में आवश्यक है।

संख्याओं का वर्गीकरण

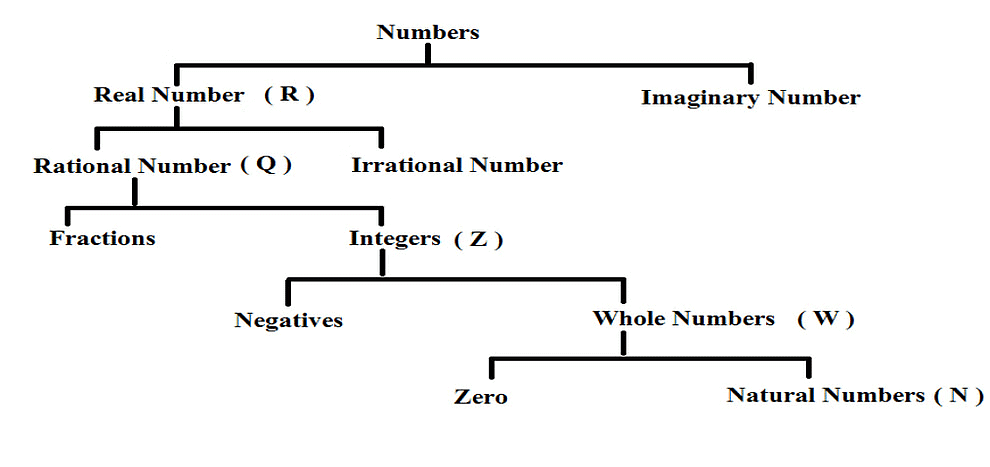
1. वास्तविक संख्याएँ और काल्पनिक संख्याएँ

वास्तविक संख्याएँ तार्किक और अतार्किक संख्याओं का समूह शामिल करती हैं।

• तार्किक संख्याएँ अंशों के रूप में व्यक्त की जा सकती हैं, जैसे -3/4 या 5/2, जबकि अतार्किक संख्याएँ, जैसे π (पाई) या √2 (2 का वर्गमूल), अंशों के रूप में नहीं व्यक्त की जा सकतीं और इनमें गैर-दोहराने वाले, गैर-समाप्त होने वाले दशमलव विस्तार होते हैं।
• वास्तविक संख्याएँ सकारात्मक या नकारात्मक, पूर्ण या भिन्न हो सकती हैं, और इन्हें संख्या रेखा पर स्थित किया जा सकता है।
• दूसरी ओर, काल्पनिक संख्याएँ काल्पनिक इकाई "i" से जुड़ी होती हैं, जहाँ i² = -1।
• जटिल संख्याएँ वास्तविक और काल्पनिक घटकों को मिलाकर बनाई जाती हैं, जिन्हें a + bi के रूप में लिखा जाता है, जहाँ 'a' और 'b' वास्तविक संख्याएँ होती हैं।
• काल्पनिक संख्याओं के उदाहरणों में 2i, -3i, और (1 + 4i) शामिल हैं।
• वास्तविक और काल्पनिक संख्याओं के बीच का संबंध गणित में जटिल विश्लेषण का आधार बनाता है।

2. तार्किक और अतार्किक संख्याएँ

तार्किक संख्याएँ

• एक तार्किक संख्या एक प्रकार की वास्तविक संख्या होती है, जो p/q के रूप में होती है, जहाँ q शून्य के बराबर नहीं होता।
• कोई भी भिन्न जिसकी हर (denominator) शून्य नहीं है, वह एक तार्किक संख्या होती है।
• तार्किक संख्याओं के कुछ उदाहरण हैं: 1/2, 1/5, 3/4, आदि।

एक संख्या जिसे एक संख्या के अनुपात के रूप में नहीं लिखा जा सकता, उसे अतार्किक संख्याएँ कहा जाता है, और इसे “P” प्रतीक द्वारा दर्शाया जाता है। उदाहरण: π (पाई), √2।

• प्राकृतिक संख्याओं के सभी वर्गमूल और घनमूल जो पूर्ण वर्ग या पूर्ण घन नहीं हैं, वे अतार्किक होते हैं।
• जोड़, घटाव, गुणन, और भाग जैसी सभी क्रियाएँ जो तार्किक संख्याओं पर लागू होती हैं, वे अतार्किक संख्याओं पर भी लागू होती हैं।
• जब एक अभिव्यक्ति में एक तार्किक और एक अतार्किक संख्या होती है, तो उन्हें समाधान के दौरान एक साथ रहना चाहिए।
• अर्थात, एक बार जब एक अतार्किक संख्या प्रकट होती है, तो इसे केवल तभी समाप्त किया जा सकता है जब इसे उसी अतार्किक संख्या से गुणा या भाग किया जाए।

3. पूर्णांक (Z)

सभी पूर्ण संख्याओं और उनके नकारात्मकों का समूह पूर्णांकों का समूह कहलाता है। इसेZ द्वारा दर्शाया जाता है, और Z = {- ∞, … - 3, - 2, - 1, 0, 1, 2, 3, ……. ∞} है।

• इन्हें नकारात्मक पूर्णांक, तटस्थ पूर्णांक और सकारात्मक पूर्णांक में वर्गीकृत किया गया है।
• (a) नकारात्मक पूर्णांक (Z-): शून्य से छोटे सभी पूर्णांकों को नकारात्मक पूर्णांक कहा जाता है। Z− = {- 1, - 2, - 3…- ∞ }
• (b) तटस्थ पूर्णांक (Z0): शून्य एकमात्र पूर्णांक है जो न तो नकारात्मक है और न ही सकारात्मक है, इसे तटस्थ पूर्णांक कहा जाता है।
• (c) सकारात्मक पूर्णांक (Z ): शून्य से बड़े सभी पूर्णांकों को सकारात्मक पूर्णांक कहा जाता है। Z = {1, 2, 3, …….., ∞ }

4. पूर्ण संख्या

संख्याओं का वह समूह जिसमें सभी प्राकृतिक संख्याएँ और शून्य शामिल हैं, उसे पूर्ण संख्याएँ कहा जाता है।

पूर्ण संख्याओं को गैर-ऋणात्मक पूर्णांक भी कहा जाता है।

5. प्राकृतिक संख्याएँ (N)

संख्याएँ 1, 2, 3, 4, 5… को प्राकृतिक संख्याएँ कहा जाता है। प्राकृतिक संख्याओं का समूह N द्वारा दर्शाया जाता है।

• सभी सकारात्मक पूर्णांक प्राकृतिक संख्याएँ हैं, और इसलिए, प्राकृतिक संख्याएँ अनंत होती हैं। इसलिए, N = {1, 2, 3, 4…}।
• प्राकृतिक संख्याएँ आगे सम, असम, प्राइम आदि में विभाजित होती हैं।
• पूर्ण संख्याएँ (W): सभी प्राकृतिक संख्याएँ और ‘0’ मिलकर पूर्ण संख्याएँ कहलाती हैं। पूर्ण संख्याओं का समूह W द्वारा दर्शाया जाता है, और W = {0, 1, 2, 3, ……}।

6. सम और असम संख्याएँ

सभी संख्याएँ जो 2 से विभाज्य होती हैं, उन्हें सम संख्याएँ कहा जाता है।

उदाहरण: 2, 4, 6, 8, 10.… सम संख्याएँ 2n के रूप में व्यक्त की जा सकती हैं, जहाँ n एक पूर्णांक है। इस प्रकार 0, -2, -6 आदि भी सम संख्याएँ हैं।

सभी संख्याएँ जो 2 से विभाज्य नहीं हैं, उन्हें असम संख्याएँ कहा जाता है।

असम संख्याएँ (2n + 1) के रूप में व्यक्त की जा सकती हैं, जहाँ n एक पूर्णांक है। उदाहरण: -1, -3, -5… 1, 3, 5, 7, 9…

7. प्राइम संख्याएँ

एक प्राकृतिक संख्या जो अपने अलावा और कोई अन्य गुणांक नहीं रखती, उसे प्राइम संख्या कहा जाता है।

उदाहरण: 2, 3, 5, 7, 11, 13, 17, 19 …

इसके विपरीत, एक संख्या जो दो से अधिक गुणांक रखती है, उसे संयोज्य संख्या कहा जाता है।

प्राइम संख्याओं के बारे में महत्वपूर्ण अवलोकन

• एक प्राइम संख्या जो 3 से बड़ी होती है, जब 6 से विभाजित की जाती है, तो शेषफल या तो 1 या 5 होता है। इसलिए, एक प्राइम संख्या को 6K ± 1 या 6K ± 5 के रूप में व्यक्त किया जा सकता है।
• लेकिन इस अवलोकन का विपरीत सत्य नहीं है, अर्थात 6 से विभाजित करते समय 1 या 5 का शेषफल देने वाली संख्या जरूरी नहीं कि प्राइम संख्या हो। उदाहरण: 25, 35 आदि।

प्राइम संख्याओं की कुछ विशेषताएँ

• सबसे छोटा प्राइम संख्या 2 है।
• संख्या 2 एकमात्र सम संख्या भी है।
• सबसे छोटी विषम प्राइम संख्या 3 है।
• जब कोई प्राइम संख्या p ≥ 5 को 6 से विभाजित किया जाता है, तो उसका शेषफल 1 या 5 होता है।
• एक प्राइम संख्या p ≥ 5 के वर्ग का 24 से विभाजन करने पर शेषफल 1 होता है।
• प्राइम संख्याओं के लिए, p > 3, p² - 1 24 से विभाज्य है।
• एक प्राइम संख्या p ≥ 5 के वर्ग का 12 से विभाजन करने पर शेषफल 1 होता है।
• यदि a और b कोई भी दो विषम प्राइम संख्या हैं, तो a² - b² और a² b² दोनों संयुक्त संख्या हैं।

किसी संख्या को प्राइम है या नहीं, यह कैसे चेक करें

किसी संख्या N को प्राइम है या नहीं, यह चेक करने के लिए निम्नलिखित प्रक्रिया अपनाएं:

• संख्या के वर्गमूल को लें।
• वर्गमूल को तुरंत उच्चतम पूर्णांक में गोल करें। इस संख्या को z कहें।
• N संख्या को z से कम सभी प्राइम संख्याओं द्वारा विभाज्यता के लिए चेक करें। यदि z के मान से कम कोई प्राइम संख्या N को विभाजित नहीं करती है, तो संख्या N प्राइम होगी।
• यदि किसी संख्या का कोई प्राइम गुणांक उसके वर्गमूल के बराबर या उससे कम नहीं है, तो वह संख्या एक प्राइम संख्या है।

उदाहरण के लिए: √239 का मान 15 और 16 के बीच है। इसलिए, z का मान 16 लें। 16 से कम प्राइम संख्याएं 2, 3, 5, 7, 11 और 13 हैं। 239 इनमें से किसी से भी विभाजित नहीं है। इसलिए, आप निष्कर्ष निकाल सकते हैं कि 239 एक प्राइम संख्या है।

प्राइम संख्याएं ढूंढना: शॉर्टकट विधि

• अधिकांश प्रतियोगिता परीक्षाओं में, यह जांचना कि कोई संख्या प्राइम है या नहीं, अक्सर 100 से 200 के बीच की 2-अंक या 3-अंक की संख्याओं पर केंद्रित होता है।
• 5 से विभाज्यता की जांच करने की आवश्यकता नहीं है क्योंकि इसे पहचानना आसान है; 5 से विभाजित संख्याएं 0 या 5 पर समाप्त होती हैं।
• इसलिए, 45 जैसी संख्या को प्राइम के रूप में गलत पहचानने का कोई जोखिम नहीं है।
• इसलिए, जब किसी संख्या के वर्गमूल से कम प्राइम संख्याओं की जांच की जा रही हो, तो 5 को परीक्षण से बाहर रखा जाता है।
• यह वही अपवाद सभी सम संख्याओं (2 को छोड़कर, जो एक प्राइम संख्या है) पर लागू होता है।

क्या कोई संख्या प्राइम है या नहीं (49 से कम संख्याओं के लिए)

49 से कम के संख्याओं के लिए, आपको केवल यह जांचना है कि संख्या 3 से विभाज्य है या नहीं। चूंकि 47 3 से विभाज्य नहीं है, यह एक प्राइम नंबर है। हम 2, 5 या 7 से विभाज्यता की जांच नहीं कर रहे हैं (7 का वर्ग 49 से अधिक है)।

121 और 49 के बीच संख्याओं की प्राइम स्थिति की जांच करना

• यह 3 और 7 से विभाज्यता की जांच करके किया जा सकता है।
• हालांकि, अगर आप याद रखें कि 77, 91, और 119 प्राइम नहीं हैं, तो आप 121 के नीचे प्राइम नंबरों की पहचान केवल 3 से विभाज्यता की जांच करके कर सकते हैं।
• यह इसलिए है क्योंकि 49 और 121 के बीच के विषम संख्याएँ जो 7 से विभाजित हैं, वे हैं 63, 77, 91, 105, और 119।
• इनमें से केवल 91 और 119 को गलती से प्राइम समझा जा सकता है। लेकिन 77 और 105 स्पष्ट रूप से प्राइम नहीं हैं।
• इसलिए, 49 और 121 के बीच संख्याओं के लिए, बस यह जांचें कि वे 3 से विभाजित हैं या नहीं। यदि नहीं हैं और वे 91 या 119 नहीं हैं, तो वे प्राइम संख्या हैं। उदाहरण के लिए, 61 प्राइम है क्योंकि यह 3 से विभाजित नहीं है और यह न तो 91 है और न ही 119।

121 और 169 के बीच संख्याओं की प्राइम स्थिति की जांच करना

• यह 3, 7 और 11 से विभाज्यता की जांच करके किया जा सकता है।
• हालांकि, यदि आप याद रखें कि 133, 143, और 161 प्राइम नहीं हैं, तो आप 121 और 169 के बीच प्राइम नंबरों की पहचान केवल 3 से विभाज्यता की जांच करके कर सकते हैं।
• यहाँ क्यों: 121 और 169 के बीच के विषम संख्याएँ जो 7 या 11 से विभाजित हैं वे हैं 133, 143, 147, 161, और 165।
• इनमें से 133, 143, और 161 को गलती से प्राइम समझा जा सकता है यदि आप 7 या 11 से विभाज्यता की जांच नहीं करते हैं।
• संख्या 147 3 से विभाज्यता की जांच करने पर प्राइम नहीं दिखाई देगी, और आप आसानी से देख सकते हैं कि 165 प्राइम नहीं है।
• इसलिए, 121 और 169 के बीच संख्याओं के लिए, आप केवल 3 से विभाज्यता की जांच करके देख सकते हैं कि संख्या प्राइम है या नहीं। उदाहरण के लिए, 149 प्राइम है क्योंकि यह 3 से विभाजित नहीं है और यह 133, 143, या 161 में से कोई नहीं है।

जानने योग्य:

• 1 से 25 ⇒ 9 प्राइम नंबर्स
• 1 से 50 ⇒ 15 प्राइम नंबर्स
• 1 से 100 ⇒ 25 प्राइम नंबर्स
• 1 से 200 ⇒ 45 प्राइम नंबर्स

8. समग्र संख्याएँ

एक समग्र संख्या में स्वयं और एकता के अलावा अन्य गुणांक होते हैं।

• हर समग्र संख्या n को इसके प्रधान गुणांकों में विभाजित किया जा सकता है। इसे इस प्रकार लिखा जा सकता है: n = p₁^m . p₂ⁿ ... p_k^s, जहाँ p₁, p₂, ..., p_k प्रधान गुणांक हैं और m, n, ..., k प्राकृतिक संख्याएँ हैं।
• उदाहरण: 24 = 2³ . 3, और 84 = 7 . 3 . 2²।
• एक समग्र संख्या का यह प्रतिनिधित्व समग्र संख्या के मानक रूप के रूप में जाना जाता है।

उदाहरण: 8, 72, 39, आदि।

• इस तथ्य के आधार पर कि एक संख्या जिसमें दो से अधिक गुणांक होते हैं, वह समग्र होती है, हमारे पास 1 से 50 तक केवल 34 समग्र संख्याएँ हैं और 51 से 100 तक 40 समग्र संख्याएँ हैं।

नोट: 1 न तो एक प्रधान संख्या है और न ही एक समग्र संख्या है।

9. पूर्ण संख्याएँ

किसी संख्या को पूर्ण संख्या कहा जाता है यदि इसके सभी गुणांकों (स्वयं को छोड़कर, लेकिन 1 को शामिल करते हुए) का योग स्वयं संख्या के बराबर हो या संख्या के सभी संभावित गुणांकों का योग दो गुना संख्या के बराबर हो।

• यदि किसी भी पूर्ण संख्या के गुणांकों को छोड़कर 1 लिखा जाता है और उनके व्युत्क्रम को एक साथ जोड़ा जाता है, तो परिणाम हमेशा एकता होता है।
• उदाहरण: 6 एक पूर्ण संख्या है क्योंकि 6 के गुणांक, अर्थात् 1, 2 और 3, संख्या 6 के बराबर होते हैं। इसके अलावा, 1/6 + 1/3 + 1/2 = (1 + 2 + 3)/6 = 6/6 = 1 (एकता)।
• अन्य पूर्ण संख्याओं के उदाहरण हैं 28, 496, 8128, आदि। अब तक 27 पूर्ण संख्याएँ खोजी गई हैं।

10. भिन्न

एक भिन्न एक इकाई के भाग या भागों को दर्शाता है।

भिन्नों के कई प्रकार होते हैं:

• सामान्य भिन्न: भिन्न जिनका हर (denominator) 10 या इसके गुणांक नहीं होते हैं। उदाहरण: 2/3, 17/18
• दशमलव भिन्न: भिन्न जिनका हर 10 या 10 के गुणांक होता है।
• सही भिन्न: इसमें अंश (numerator) < हर="" होता="" है।="" उदाहरण:="" 2/10,="" 6/7,="" 8/9="" आदि।="" इसलिए="" इसका="" मान="" />< 1="" होता="" />
• असामान्य भिन्न: इनमें अंश > हर होता है। उदाहरण: 10/2, 7/6, 8/7 आदि। इसलिए इसका मान > 1 होता है।
• मिश्रित भिन्न: जब एक असामान्य भिन्न को एक पूर्णांक और एक सही भिन्न के रूप में लिखा जाता है, तो इसे मिश्रित भिन्न कहा जाता है। उदाहरण: 7/3 को 2 1/3 = 2(1/3) के रूप में लिखा जा सकता है।

11. दशमलव संख्या

एक दशमलव संख्या वह संख्या होती है जिसमें दशमलव बिंदु होता है। उदाहरण: 1.5, 3.22, 829.234

• जब हम किसी संख्या को किसी अन्य संख्या से विभाजित करते हैं, तो हमें या तो समाप्ति दशमलव भिन्न प्राप्त होती है या गैर-समाप्ति दशमलव भिन्न।
• समाप्ति दशमलव भिन्न: वे संख्याएँ होती हैं जिनमें दशमलव बिंदु के बाद निश्चित या सीमित संख्या के अंक होते हैं।
• गैर-समाप्ति दशमलव भिन्न: दशमलव के बाद अंकों की उपस्थिति के आधार पर इसे निम्नलिखित प्रकारों में वर्गीकृत किया जा सकता है:
  • शुद्ध पुनरावर्ती दशमलव: एक दशमलव जिसमें दशमलव बिंदु के बाद सभी अंक पुनरावृत्त होते हैं, इसे शुद्ध पुनरावर्ती दशमलव कहते हैं। उदाहरण: 0.333...।
  • मिश्रित पुनरावर्ती दशमलव: एक दशमलव जिसमें कुछ अंक पुनरावृत्त नहीं होते और कुछ पुनरावृत्त होते हैं, इसे मिश्रित पुनरावर्ती दशमलव कहते हैं। उदाहरण: 0.1666...।
  • गैर-पुनरावर्ती दशमलव: एक दशमलव संख्या जिसमें अंक किसी पैटर्न में पुनरावृत्त नहीं होते हैं, इसे गैर-समाप्ति गैर-पुनरावर्ती दशमलव कहा जाता है और इसे अव्यक्तीय संख्या कहा जाता है।

पुनरावर्ती भिन्न को दशमलव में परिवर्तित करना:

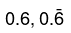
सभी आवर्ती दशमलवों को भिन्नों में परिवर्तित किया जा सकता है। कुछ सामान्य प्रकार हो सकते हैं: 0.33….., 0.1232323…, 5.33…., 14.23636363…. आदि।

(a) शुद्ध आवर्ती से भिन्नों में

फंडा 1: यदि कोई संख्या 0. ababab……. के रूप में है, तो आवर्ती अंकों को उस संख्या के अनुसार 9 से विभाजित करें जितने आवर्ती अंक हैं। उदाहरण: 0.363636... = 36/99 = 4/11

(b) मिश्रित आवर्ती से भिन्नों में

फंडा 2: यदि N = 0. abcbcbc…. तो N = abc - a/990 = आवर्ती और गैर आवर्ती अंक - गैर आवर्ती अंक / जितने 9's आवर्ती अंकों के हैं उसके बाद उतने 0's गैर आवर्ती अंकों के। उदाहरण: 0.25757... = 257 - 2/990 = 255/990 = 17/66

फंडा 3: यदि N = a. bcbc…. तो N = a + 0. bcbc…. का उपयोग करें। फंडा 1 के अनुसार आगे बढ़ें। उदाहरण: 5.3636… = 5 + 0.3636… = 5 + 36/99 = 59/11

12. संख्या रेखा का सिद्धांत

संख्या रेखा एक सीधी रेखा है जो दोनों दिशाओं में अनंत तक फैली हुई है, जिसमें बाईं ओर नकारात्मक अनंत और दाईं ओर सकारात्मक अनंत है।

• संख्या रेखा पर किसी भी दो बिंदुओं के बीच की दूरी को उच्चतम मान से निम्नतम मान को घटाकर प्राप्त किया जाता है।
• एक अन्य तरीका यह है कि छोटे संख्या से शुरू करें और देखें कि बड़े संख्या तक पहुँचने के लिए कितना जोड़ना है। उदाहरण: 7 और –4 के बीच की दूरी 7 – (–4) = 11 है।

भाज्यता

• जैसा कि नाम से स्पष्ट है, भाज्यता परीक्षण या विभाजन नियम गणित में किसी संख्या को बिना वास्तविक विभाजन विधि के द्वारा यह जांचने में सहायता करते हैं कि क्या एक संख्या दूसरे संख्या द्वारा विभाज्य है।
• एक संख्या x को दूसरी संख्या y द्वारा तब भाज्य माना जाता है जब x को y से बिना किसी शेषफल के विभाजित किया जा सके।
• सामान्यतः, जब एक पूर्णांक 𝐼 को एक प्राकृतिक संख्या 𝑁 से विभाजित किया जाता है, तो 𝑄 (कोटिएंट) और 𝑅 (शेषफल) की एक अनोखी जोड़ी होती है। इसे इस प्रकार व्यक्त किया जा सकता है: 𝐼 = 𝑄𝑁 + 𝑅
• किसी भी पूर्णांक 𝐼 और किसी भी प्राकृतिक संख्या 𝑁 के लिए, 𝑄 और 𝑅 की एक अनोखी जोड़ी होती है ताकि 𝐼 = 𝑄𝑁 + 𝑅 हो, जहाँ 𝑄 एक पूर्णांक है, 𝑁 एक प्राकृतिक संख्या (या शून्य) है, और 0 ≤ 𝑅 < 𝑁="" (जिसका="" अर्थ="" है="" कि="" शेषफल="" 𝑁="" से="" कम="" होना="" चाहिए)।="" यदि="" शेषफल="" 𝑅="" शून्य="" है,="" तो="" हम="" कहते="" हैं="" कि="" 𝐼,="" 𝑁="" से="" भाज्य="" />

नोट: जब हम किसी नकारात्मक संख्या को प्राकृतिक संख्या N से विभाजित करते हैं, तो शेषफल हमेशा गैर-नकारात्मक रहता है। उदाहरण के लिए, जब हम –32 को 7 से विभाजित करते हैं, तो शेषफल वास्तव में 3 होता है, न कि –4, जो हैरान करने वाला हो सकता है। यह इसलिए है क्योंकि शेषफल हमेशा गैर-नकारात्मक होता है। इसलिए, जब हम –32 को 7 से विभाजित करते हैं, तो कोटिएंट –5 है और शेषफल 3 है।

भाग करने के प्रमेय

भाग्यता के नियम

1. 1 का भाग्यता नियम

• हर संख्या 1 से भाग दिया जा सकता है। 1 के लिए भाग्यता नियम में कोई शर्त नहीं है। किसी भी संख्या को 1 से भाग देने पर वही संख्या प्राप्त होती है, चाहे संख्या कितनी भी बड़ी हो। उदाहरण: 3 को 1 से भाग दिया जा सकता है और 3000 को भी 1 से पूरी तरह से भाग दिया जा सकता है।

2. 2 का भाग्यता नियम

• यदि कोई संख्या सम है या उस संख्या का अंतिम अंक सम संख्या है यानी 2, 4, 6, 8 जिसमें 0 भी शामिल है, तो यह हमेशा 2 से पूरी तरह से भाग्य है। उदाहरण: 508 एक सम संख्या है और 2 से भाग दिया जा सकता है लेकिन 509 नहीं। 508 की 2 से भाग्यता की जांच करने की प्रक्रिया इस प्रकार है: ⇒ संख्या 508 पर विचार करें ⇒ केवल अंतिम अंक 8 लें और उसे 2 से भाग दें ⇒ यदि अंतिम अंक 8, 2 से भाग जाता है, तो संख्या 508 भी 2 से भाग जाती है।

3. 3 के लिए भाग्यता नियम

• 3 के लिए भाग्यता नियम यह कहता है कि कोई संख्या तभी पूरी तरह से 3 से भाग्य होगी जब उसके अंकों का योग 3 से भाग्य हो। उदाहरण: एक संख्या पर विचार करें, 308। यह जांचने के लिए कि क्या 308, 3 से भाग्य है या नहीं, अंकों का योग लें (यानी 3 + 0 + 8 = 11)। अब जांचें कि क्या योग 3 से भाग्य है। यदि योग 3 का गुणांक है, तो मूल संख्या भी 3 से भाग्य है। यहाँ, चूंकि 11, 3 से भाग्य नहीं है, 308 भी 3 से भाग्य नहीं है। इसी तरह, 516 पूरी तरह से 3 से भाग्य है क्योंकि इसके अंकों का योग यानी 5 + 1 + 6 = 12, 3 का गुणांक है।

4. 4 का भाग्यता नियम

यदि संख्या के अंतिम दो अंक 4 से विभाज्य हैं, तो वह संख्या 4 का गुणज है और पूरी तरह से 4 से विभाज्य है।

• उदाहरण: संख्या 2308 लें। अंतिम दो अंकों पर विचार करें, अर्थात् 08। चूंकि 08, 4 से विभाज्य है, इसलिए मूल संख्या 2308 भी 4 से विभाज्य है।

5. 5 का विभाज्यता नियम

• संख्याएँ, जो 0 या 5 पर समाप्त होती हैं, हमेशा 5 से विभाज्य होती हैं।
• उदाहरण: 10, 10000, 10000005, 595, 396524850, आदि।

6. 6 का विभाज्यता नियम

• संख्याएँ जो 2 और 3 दोनों से विभाज्य हैं, वे 6 से भी विभाज्य होती हैं। अर्थात्, यदि दी गई संख्या का अंतिम अंक सम है और उसके अंकों का योग 3 का गुणज है, तो दी गई संख्या 6 का गुणज भी है।
• उदाहरण: 630, यह संख्या 2 से विभाज्य है क्योंकि अंतिम अंक 0 है। अंकों का योग 6 + 3 + 0 = 9 है, जो 3 से भी विभाज्य है। इसलिए, 630, 6 से विभाज्य है।

7. 7 के लिए विभाज्यता नियम

7 से विभाज्यता का नियम थोड़ा जटिल है जिसे निम्नलिखित चरणों द्वारा समझा जा सकता है:

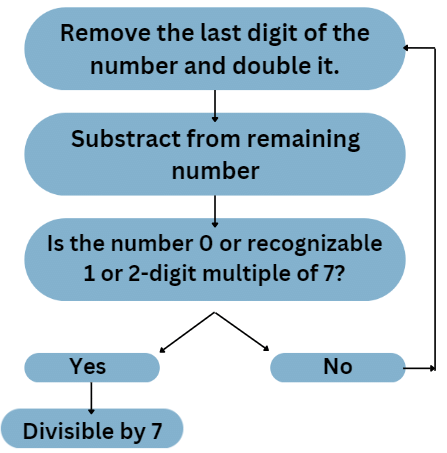
उदाहरण: क्या 1073, 7 से विभाज्य है?

• उपरोक्त नियम से 3 को संख्या से हटा दें और इसे दोगुना करें, जो 6 बनता है। शेष संख्या 107 हो जाती है, तो 107 - 6 = 101। एक और बार प्रक्रिया को दोहराते हैं, हमें 1 x 2 = 2 मिलता है। शेष संख्या 10 - 2 = 8। चूंकि 8, 7 से विभाज्य नहीं है, इसलिए संख्या 1073, 7 से विभाज्य नहीं है।

8. 8 का विभाज्यता नियम

• यदि किसी संख्या के अंतिम तीन अंक 8 से विभाज्य हैं, तो वह संख्या पूरी तरह से 8 से विभाज्य है।
• उदाहरण: संख्या 24344 लें। अंतिम तीन अंकों पर विचार करें, अर्थात् 344। चूंकि 344, 8 से विभाज्य है, इसलिए मूल संख्या 24344 भी 8 से विभाज्य है।

9. 9 का विभाज्यता नियम

9 का विभाजन नियम

• 9 के लिए विभाजन का नियम 3 के लिए विभाजन नियम के समान है। अर्थात, यदि किसी संख्या के अंकों का योग 9 से विभाज्य है, तो वह संख्या भी 9 से विभाज्य है।
• उदाहरण: 78532 पर विचार करें, इसके अंकों का योग (7 + 8 + 5 + 3 + 2) 25 है, जो 9 से विभाज्य नहीं है, इसलिए 78532 भी 9 से विभाज्य नहीं है।

10 का विभाजन नियम

• 10 के लिए विभाजन का नियम कहता है कि कोई भी संख्या जिसकी अंतिम अंक 0 हो, वह 10 से विभाज्य है।
• उदाहरण: 10, 20, 30, 1000, 5000, 60000, आदि।

11 का विभाजन नियम

यदि किसी संख्या के वैकल्पिक अंकों के योग का अंतर 11 से विभाज्य है, तो वह संख्या पूर्ण रूप से 11 से विभाज्य है।

जैसे कि 2143 संख्या की जांच करने के लिए, नीचे की प्रक्रिया का पालन करें:

• वैकल्पिक अंकों को समूहित करें, अर्थात, विषम स्थानों पर अंकों को एक साथ और सम स्थानों पर अंकों को एक साथ रखें। यहाँ 24 और 13 दो समूह हैं।
• प्रत्येक समूह के अंकों का योग लें, अर्थात 2 + 4 = 6 और 1 + 3 = 4।
• योगों का अंतर निकालें; 6 - 4 = 2।
• यदि अंतर 11 से विभाज्य है, तो मूल संख्या भी 11 से विभाज्य होगी। यहाँ 2 अंतर है जो 11 से विभाज्य नहीं है। इसलिए, 2143 11 से विभाज्य नहीं है।

12 का विभाजन नियम

• यदि संख्या 3 और 4 दोनों से विभाज्य है, तो वह संख्या 12 से भी पूरी तरह से विभाज्य है।
• उदाहरण: 5864 ⇒ अंकों का योग = 5 + 8 + 6 + 4 = 23 (3 का गुणांक नहीं है) ⇒ अंतिम दो अंक = 64 (4 से विभाज्य) ⇒ दी गई संख्या 5846 4 से विभाज्य है लेकिन 3 से नहीं; इस प्रकार, यह 12 से विभाज्य नहीं है।

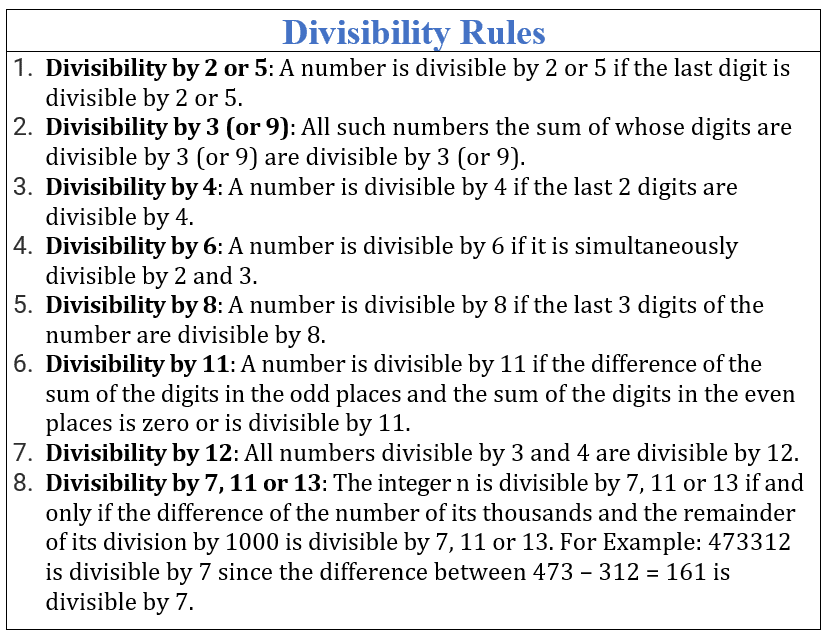
13 का विभाजन नियम

किसी दिए गए संख्या के लिए, यह जाँचने के लिए कि क्या यह 13 से विभाज्य है, हमें संख्या के अंतिम अंक का चार गुना शेष संख्या में जोड़ना होता है और इस प्रक्रिया को तब तक दोहराना होता है जब तक हमें एक दो अंकों की संख्या न मिले। अब जाँच करें कि वह दो अंकों की संख्या 13 से विभाज्य है या नहीं। यदि यह विभाज्य है, तो दी गई संख्या 13 से विभाज्य है।

• उदाहरण: 2795 ⇒ 279 (5 x 4) ⇒ 279 (20) ⇒ 299 ⇒ 29 (9 x 4) = 29 36 = 65। संख्या 65 13 से विभाज्य है, 13 x 5 = 65।

संख्याओं के गुण

• प्रत्येक संख्या की पाँचवीं शक्ति में उसका इकाई अंक उसी प्रकार होता है जैसे उसकी पहली शक्ति में होता है। इसलिए, जो मानक विधि अपनाई जा सकती है, वह है दी गई शक्ति को 4 से विभाजित करना, शेष शक्ति को खोजना और उस संख्या में इकाई अंक की जाँच करना। यह शॉर्टकट इसलिए लागू किया जा सकता है क्योंकि आपको हमेशा वही इकाई अंक मिलेगा।
• किसी संख्या के फैक्टोरियल के अंत में शून्य की संख्या की गणना करने के लिए, आपको संख्या को 5 से विभाजित करना चाहिए, प्राप्त भाग को फिर से 5 से विभाजित करना चाहिए और इसी तरह तब तक करना चाहिए जब तक अंतिम भाग 5 से छोटा न हो जाए। सभी भागों का योग 5 की संख्या है, जो दी गई संख्या में शून्य की संख्या बन जाती है।
• किसी संख्या की डिजिटल रूट वह है जो अंकों का योग है, बार-बार, जब तक यह एक अंकीय संख्या नहीं बन जाती। उदाहरण के लिए, 87984 की डिजिटल रूट होगी 8 + 7 + 9 + 8 + 4 ⇒ 36 = 3 + 6 ⇒ 9।
• जब यूलेर संख्या का सिद्धांत लागू होता है और भाजक और भाज्य सह-प्राइम होते हैं, तो शेष प्रश्न बहुत आसान हो जाते हैं।
• तीन लगातार प्राकृतिक संख्याओं का उत्पाद 6 से विभाज्य होता है। उदाहरण के लिए, मान लीजिए n, n + 1, और n + 2 तीन लगातार प्राकृतिक संख्याएँ हैं और P(n) उनका उत्पाद है। तब, P(n) = n(n + 1)(n + 2)।
• हमारे पास, P(1) = 1×2×3 = 6, जो 3 और 6 से विभाज्य है। P(2) = 2×3×4 = 24, जो 3, 8 और 6 से विभाज्य है। P(3) = 3×4×5 = 60, जो 3 और 6 से विभाज्य है। P(4) = 4×5×6 = 120, जो 3, 8 और 6 से विभाज्य है। इसलिए, P(n) सभी n ∈ N के लिए 3 और 6 से विभाज्य है।
• तीन लगातार प्राकृतिक संख्याओं का उत्पाद, जिसमें से पहली संख्या सम होती है, 24 से विभाज्य होता है।
• एक दो-अंकीय संख्या और उसकी अंकों को उलटकर बनाई गई संख्या का योग 11 से विभाज्य होता है।
• xn - yn = (x + y) (xn-1 - xn-2.y ... yn-1) जब n सम हो। इसलिए, जब n सम हो, xn - yn x + y से विभाज्य होता है। उदाहरण: 72 - 32 = 40, जो 10 से विभाज्य है, जो (7 + 3) है।
• xn - yn = (x - y) (xn-1 xn-2.y ... yn-1) दोनों विषम और सम n के लिए। इसलिए, xn - yn x - y से विभाज्य होता है। उदाहरण: 94 - 24 = 6545, जो 7 से विभाज्य है, जो (9 – 2) है।

संख्या का पूर्णांक मान

संख्याओं का मापांक किसी संख्या का मापांक उस संख्या का अभ्युत्तम मान होता है, या हम कह सकते हैं कि यह संख्या की मूल से दूरी है। किसी संख्या का अभ्युत्तम मान इस प्रकार परिभाषित किया गया है: |a| = a, यदि a ≥ 0 = - a, यदि a ≤ 0 |a| को मापांक (MODULUS) के रूप में पढ़ा जाता है।
उदाहरण: |79| = 79 और | -45| = - (-45) = 45। इसके अलावा, | x - 3 | = x - 3, यदि x ≥ 3 = 3 - x, यदि x < />।

हल किए गए उदाहरण

उदाहरण 1: N = (18n² + 9n + 8)/n; जहाँ N पूर्णांक है। N के कितने पूर्णांक समाधान संभव हैं?

दी गई अभिव्यक्ति को इस प्रकार तोड़ा जा सकता है: 18n²/n + 9n/n + 8/n। इससे हमें प्राप्त होता है: 18n + 9 + 8/n।

• अब हम देख सकते हैं कि ‘n’ का कोई भी मान हो, 18n + 9 हमेशा एक पूर्णांक मान देगा। इसलिए, यह अब 8/n पर निर्भर करता है केवल ⇒ n का कोई भी पूर्णांक मान हो सकता है, जो 8 का गुणांक है।
• जो पूर्णांक इस शर्त को पूरा करेंगे वे हैं ±1, ±2, ±4, ±8। इसलिए, कुल मिलाकर, n 8 मान ले सकता है।

उदाहरण 2: N = 960। N के कुल गुणांक ज्ञात करें।

• संयुक्त संख्या के गुणांक: यदि D एक संयुक्त संख्या है जो इस रूप में है D = a^p × b^q × c^r, जहाँ a, b, c प्राथमिक हैं, तो D के गुणांक की संख्या, जिसे n द्वारा दर्शाया गया है, इस प्रकार दी गई है: n = (p + 1)(q + 1)(r + 1)।
• इसी प्रकार, 960 को प्राथमिक गुणांकों में विभाजित करने के बाद: 2⁶ × 3¹ × 5¹, हम कुल गुणांकों की संख्या इस प्रकार ज्ञात कर सकते हैं: (6 + 1)(1 + 1)(1 + 1) = 28।

उदाहरण 3: निम्नलिखित अभिव्यक्ति का इकाई अंक ज्ञात करें: (123)³⁴ × (876)⁴⁵⁶ × (45)⁸⁶.

जब भी एक सम इकाई अंक संख्या और एक 5 वाले इकाई अंक संख्या मौजूद होती है, तो वे हमेशा इकाई अंक में 0 देंगे, चाहे अन्य कोई संख्या मौजूद हो या न हो।

• जब भी एक सम इकाई अंक संख्या और एक 5 वाले इकाई अंक संख्या मौजूद होती है, तो वे हमेशा इकाई अंक में 0 देंगे, चाहे अन्य कोई संख्या मौजूद हो या न हो।

उदाहरण 4. पहले 100 प्राकृतिक संख्याओं के गुणनफल के अंत में शून्य की संख्या क्या होगी?

उदाहरण 5. संख्या 2347$98 में $ के स्थान पर कौन सा अक्षर होना चाहिए, ताकि यह 9 का गुणज बन जाए?

• जैसा कि आप जानते हैं कि यदि सभी अंकों का योग 9 से विभाज्य है, तो संख्या 9 से विभाज्य होती है। अब दिए गए अंकों का योग है 2 + 3 + 4 + 7 + 9 + 8 = 33 $। अब 33 के बाद का अगला 9 का गुणज सोचें, यानी 36। इसका मतलब है कि आपको इसमें 3 जोड़ना है। $ का मान 3 है।

उदाहरण 6. एक पार्टी में 20 लोग उपस्थित हैं। यदि उनमें से प्रत्येक अन्य सभी व्यक्तियों के साथ हाथ मिलाता है, तो कुल मिलाकर कितनी बार हाथ मिलाए जाएंगे?

• 20 व्यक्तियों में, पहला व्यक्ति 19 व्यक्तियों के साथ हाथ मिलाएगा। दूसरा व्यक्ति 18 व्यक्तियों के साथ हाथ मिलाएगा (क्योंकि उसने पहले व्यक्ति के साथ पहले ही हाथ मिला लिया है)। तीसरा व्यक्ति 17 व्यक्तियों के साथ हाथ मिलाएगा और इसी तरह। दूसरा अंतिम व्यक्ति केवल एक व्यक्ति के साथ हाथ मिलाएगा। और अंतिम व्यक्ति किसी के साथ हाथ नहीं मिलाएगा (क्योंकि उसने सभी व्यक्तियों के साथ पहले ही हाथ मिला लिया है)। कुल हाथ मिलाने की संख्या जानने के लिए, आपको 1 से 19 तक सभी प्राकृतिक संख्याओं को जोड़ना होगा, यानी ∑ 19। ∑19 = 19 x 20/2 = 190 हाथ मिलाने होंगे।

उदाहरण 7. जब 2354789341 को 11 से विभाजित किया जाता है, तो शेषफल क्या होगा?

विषम स्थान के अंक का योग (O) = 1 3 8 4 3 = 19।

सम स्थान के अंकों का योग (E) = 4 9 7 5 2 = 27।

अंतर (D) = 19 - 27 = - 8

शेषफल = 11 - 8 = 3।

• विषम स्थान के अंक का योग (O) = 1 3 8 4 3 = 19।
• सम स्थान के अंकों का योग (E) = 4 9 7 5 2 = 27।

टिप: जब किसी संख्या को उसके पलटे हुए रूप में जोड़ा जाता है, तो उस संख्या का योग हमेशा 11 से विभाज्य होता है। उदाहरण: 2341 + 1432 = 3773, जो 11 से विभाज्य है।

⇒ कोई भी संख्या यदि 6 बार लगातार लिखी जाए तो वह 7 और 13 से विभाज्य होगी।

उदाहरण 8: यदि 567P55Q 88 से विभाज्य है; P और Q का मान ज्ञात करें। (a) 11 (b) 12 (c) 5 (d) 6 (e) 10

सही उत्तर विकल्प (e) है।

• संख्या 8 से विभाज्य है, इसका अर्थ है कि अंतिम 3 अंकों द्वारा बनाई गई संख्या 8 से विभाज्य होनी चाहिए, जो हैं 55 Q। केवल Q = 2 इस शर्त को पूरा करता है।
• 11 के विभाजन नियम के अनुसार, (2 5 7 5) - (5 P 6) 11 से विभाज्य है। इसलिए 8-P 11 से विभाज्य होना चाहिए।
• यदि P= 8 है, तो ही यह संभव है। इसलिए P = 8 और Q = 2। अतः, P Q = 10।

उदाहरण 9: यदि पहले 100 प्राकृतिक संख्याओं को एक साथ लिखकर एक बड़ी संख्या बनाई जाए और उसे 8 से विभाजित किया जाए। शेषफल क्या होगा?

(a) 1 (b) 2 (c) 4 (d) 7 (e) ज्ञात नहीं किया जा सकता

सही उत्तर विकल्प (c) है।

• संख्या है 1234…..9899100।
• 8 के विभाजन नियम के अनुसार, हम केवल अंतिम 3 अंकों की जांच करेंगे। यदि 100 को 8 से विभाजित किया जाए, तो शेषफल 4 होगा।

उदाहरण 10: जब 4444……..44 बार को 7 से विभाजित किया जाएगा तो शेषफल क्या होगा? (a) 1 (b) 2 (c) 5 (d) 6 (e) 0

सही उत्तर विकल्प (b) है।

• यदि 4 को 7 से विभाजित किया जाए, तो शेषफल 4 होगा।
• यदि 44 को 7 से विभाजित किया जाए, तो शेषफल 2 होगा।
• यदि 444 को 7 से विभाजित किया जाए, तो शेषफल 3 होगा।
• इस तरह जांच करने पर हमें पता चलता है कि 444444 7 से बिल्कुल विभाज्य है।
• तो यदि हम छह 4 लें, तो यह 7 से बिल्कुल विभाज्य है।
• इसी तरह, बारह 4 भी 7 से बिल्कुल विभाज्य है और 42 4 भी 7 से बिल्कुल विभाज्य होंगे।
• तो 44 में से शेष दो 4, शेषफल 2 देंगे।

सह-प्राइम या तुलनात्मक रूप से प्राइम संख्याएँ

दो या दो से अधिक संख्याएँ जो कोई सामान्य गुणांक साझा नहीं करती हैं, उन्हें सह-प्राइम या तुलनात्मक रूप से प्राइम कहा जाता है। दूसरे शब्दों में, उनका सबसे बड़ा सामान्य गुणांक 1 होता है।

यदि दो संख्याएँ m और n तुलनात्मक रूप से प्राइम हैं, और एक प्राकृतिक संख्या x m और n दोनों के लिए व्यक्तिगत रूप से विभाज्य है, तो x भी mn द्वारा विभाज्य होगा।

मुख्य अवधारणा 1: जब दो संख्याएँ भिन्नों के हर में उपस्थित होती हैं, तब उन्हें सह-प्राइम के रूप में पहचानना महत्वपूर्ण है।

• इस अवधारणा को एक उदाहरण द्वारा सबसे अच्छा समझाया जा सकता है: मान लीजिए M/8 और N/9, जहाँ M 8 से विभाजित नहीं है और N 9 से विभाजित नहीं है। ये संख्याएँ सह-प्राइम हैं, जिसका अर्थ है कि उनके पास 1 के अलावा कोई सामान्य गुणांक नहीं है। जब दो संख्याएँ सह-प्राइम होती हैं, तो परिणाम दशमलव भिन्न होता है, न कि पूर्णांक। इसका कारण यह है कि 8 और 9 सह-प्राइम हैं, और सह-प्राइम संख्याओं द्वारा विभाजित करने पर दशमलव परिणाम एक-दूसरे से मेल नहीं खाते। यह अवधारणा समस्याओं को हल करते समय अत्यधिक महत्वपूर्ण होती है, विशेषकर शब्द समस्याओं में रैखिक समीकरणों के साथ।

उदाहरण: 36 से विभाज्य चार अंकों की संख्याओं का पता लगाएँ जो 25x7y के रूप में हैं।

समाधान: चूंकि 36 दो सह-प्राइम संख्याओं, 4 और 9 का गुणनफल है, संख्या 25x7y को 36 से विभाज्य होने के लिए दोनों 4 और 9 से विभाज्य होना चाहिए।

• 4 से विभाज्यता: 4 से विभाज्यता के लिए, संख्या के अंतिम दो अंक (7y) 4 से विभाज्य होने चाहिए। 7y को 4 से विभाज्य बनाने के लिए संभावित मान y के 2 और 6 हैं। इसलिए, y 2 या 6 हो सकता है।
• 9 से विभाज्यता: 9 से विभाज्यता के लिए, संख्या के अंकों का योग 9 से विभाज्य होना चाहिए। अंकों का योग है 2 5 x 7 y। यदि y=2, तो योग होगा 2 5 x 7 2=16 x। इसके 9 से विभाज्य होने के लिए, 16 x को 9 का गुणज होना चाहिए। x का संभावित मान 2 है (क्योंकि 16 2 = 18, जो 9 से विभाज्य है)। यदि y=6, तो योग होगा 2 5 x 7 6=20 x। इसके 9 से विभाज्य होने के लिए, 20 x को 9 का गुणज होना चाहिए। x का संभावित मान 7 है (क्योंकि 27 9 से विभाज्य है)।

इस प्रकार, संख्याएँ 25272 और 25776, 36 से विभाज्य हैं।

मुख्य अवधारणा 2: यह निर्धारित करने का एक और तरीका कि क्या दो संख्याएँ सह-प्राइम हैं, उनके प्राथमिक गुणांक की जाँच करना है। दो या अधिक संख्याएँ सह-प्राइम होने के लिए, उनके प्राथमिक गुणांक में कोई सामान्य तत्व नहीं होना चाहिए।

उदाहरण के लिए, यदि A और B सह-प्राथमिक हैं, और A = 2ⁿ 3^m है, तो B के गुणनखंडों में 2 या 3 शामिल नहीं होने चाहिए। इसके बजाय, यह 5, 7, 11 आदि जैसे अन्य प्राथमिक संख्याओं से बना होगा, लेकिन इसमें 2 या 3 गुणनखंड के रूप में नहीं हो सकते।

हमेशा ध्यान में रखें

• संख्या 1 न तो प्राथमिक है और न ही समुच्चय।
• 2 एकमात्र सम संख्या है जो प्राथमिक है।
• (xⁿ yⁿ) (x y) द्वारा विभाज्य है, जब n एक विषम संख्या है।
• (xⁿ - yⁿ) (x y) द्वारा विभाज्य है, जब n एक सम संख्या है।
• (xⁿ - yⁿ) (x - y) द्वारा विभाज्य है, जब n एक विषम या सम संख्या है।
• 5 लगातार पूर्ण संख्याओं का योग हमेशा 5 द्वारा विभाज्य होगा।
• दो संख्याओं का अंतर (xy) - (yx) हमेशा 9 द्वारा विभाज्य होगा।
• एक विषम संख्या का वर्ग 8 द्वारा विभाजित करने पर हमेशा 1 शेष देता है।
• प्रत्येक वर्ग संख्या 3 का गुणांक या 3 के गुणांक से 1 अधिक होती है।
• प्रत्येक वर्ग संख्या 4 का गुणांक या 4 के गुणांक से 1 अधिक होती है।
• यदि एक वर्ग संख्या 9 पर समाप्त होती है, तो पूर्ववर्ती अंक सम होता है।
• यदि m और n दो पूर्णांक हैं, तो (m n)! m! n! द्वारा विभाज्य है।
• (a)ⁿ / (a - 1) शेष छोड़ता है।
• n लगातार संख्याओं का गुणन हमेशा n! द्वारा विभाज्य होता है।

उदाहरण 1: यदि ‘X’ एक सम संख्या है; Y एक विषम संख्या है, तो निम्नलिखित में से कौन सा सम है? (a) X² Y (b) X Y² (c) X² Y² (d) X² Y² (e) इनमें से कोई नहीं

सही उत्तर विकल्प (d) है।

• चूंकि X सम है, X² सम है। Y विषम है, Y² विषम है।
• इसलिए विकल्प (1), (2), (3) सम विषम = विषम हैं।
• विकल्प (4) है (सम) (विषम) = सम।

उदाहरण 2: 0.343434.... और 0.2343434…… के बीच का अंतर भिन्न रूप में क्या है?

• (a) 6/55
• (b) 6/11
• (c) 9/55
• (d) 9/13
• (e) 5/11

सही उत्तर विकल्प (a) है। 0.343434..... = 34/99 और 0.23434.... = 234 - 2/990 = 232/990 ∴ अंतर = 34/99 - 232/990 = 108/990 = 6/55

उदाहरण 3: निम्नलिखित संख्याओं में से कितनी कम से कम 3 विभिन्न प्राइम नंबर द्वारा विभाज्य हैं: 231, 750, 288 और 1372?

• (a) 0
• (b) 1
• (c) 2
• (d) 3
• (e) 4

• 231 = 3 × 7 × 11 (3 प्राइम फैक्टर)
• 750 = 2 × 3 × 5³ (3 प्राइम फैक्टर)
• 288 = 2⁵ × 3² (केवल 2 प्राइम फैक्टर)
• 1372 = 2² × 7³ (केवल 2 प्राइम फैक्टर)
• इसलिए, केवल 231 और 750 में 3 प्राइम फैक्टर हैं।

उदाहरण 4: n³ - 6n² + 11n - 6 (जहां n एक पूर्ण संख्या है) हमेशा किससे विभाज्य है?

• (a) 4
• (b) 5
• (c) 6
• (d) 8
• (e) 12

• n³ - 6n² + 11n - 6 = (n - 1)(n - 2)(n - 3)।
• तीन लगातार संख्याओं का गुणनफल हमेशा 3! = 6 से विभाज्य होता है। (या) n = 0, 1, 2, 3 लेकर देखें, यह हमेशा 6 से विभाज्य है।

उदाहरण 5: यदि 351 × 352 × 353 × ... × 356 को 360 से विभाजित किया जाए, तो शेषफल क्या होगा?

• (a) 0
• (b) 1
• (c) 2
• (d) 3
• (e) 359

• चूंकि दिया गया 6 लगातार संख्याओं का गुणनफल है, यह हमेशा 6! = 720 से विभाज्य होता है।
• यह 360 से भी विभाज्य है। इसलिए, शेषफल 0 होगा।

HCF और LCM की अवधारणाएँ
सर्वाधिक सामान्य गुणांक (HCF)

सर्वाधिक समान गुणांक (HCF) और न्यूनतम समापवर्त्य (LCM) के अवधारणाएँ

• समान गुणांक: यदि दो संख्याएँ A और B किसी संख्या X द्वारा पूरी तरह विभाजित होती हैं, तो X A और B का समान भाजक या गुणांक है।
• सर्वाधिक समान गुणांक: यह दो या अधिक संख्याओं का सर्वोच्च गुणांक है जो विचाराधीन हैं। इसे GCF या GCD (सर्वाधिक समान गुणांक या सर्वाधिक समान भाजक) भी कहा जाता है। उदाहरण: 4 और 8 का HCF = 4, 125 और 200 का HCF = 25।

दी गई संख्याओं का HCF खोजने की प्रक्रिया:

• 1. दी गई संख्याओं को उनके मूल गुणांकों में तोड़ें।
• 2. HCF सभी संख्याओं में समान मूल गुणांकों का गुणनफल होगा।

आइए कुछ हल किए गए उदाहरणों की मदद से HCF खोजने की प्रक्रिया सीखते हैं।

प्रश्न: 96, 36 और 18 का HCF खोजें।

हल: पहले प्रत्येक संख्या को उनके मूल गुणांकों में तोड़ें। 96 = 2 x 3 x 2 x 2 x 2 x 2 36 = 2 x 3 x 2 x 3 18 = 2 x 3 x 3 इन संख्याओं के सभी समान गुणांकों को लें और उनका गुणन करें। इसलिए, 96, 36 और 18 का HCF उन सभी संख्याओं में समान गुणांकों का सबसे बड़ा गुणनफल है, अर्थात्, 2 x 3 = 6। दूसरे शब्दों में, 6 वह सबसे बड़ा पूर्णांक है, जो 96, 36 और 18 को बिना किसी शेष के विभाजित कर सकता है।

प्रश्न: 42 और 70 का HCF खोजें।

हल: 42 = 3 x 2 x 7 70 = 5 x 2 x 7 इसलिए, HCF = 2 x 7 = 14।

प्रश्न: 144, 630 और 756 का HCF खोजें।

हल: 144 = 24 x 32 630 = 2 x 32 x 5 x 7 756 = 22 x 33 x 7 इसलिए, 144, 630, 756 का HCF = 2 x 32 = 18।

महत्वपूर्ण:

• दो अभाज्य संख्याओं का HCF हमेशा 1 होता है।
• सह-प्राइम संख्याओं का HCF हमेशा 1 होता है।

HCF खोजने की शॉर्टकट विधि

आइए उदाहरणों का उपयोग करके संख्याओं के सेट का HCF (उच्चतम सामान्य गुणांक) खोजने का एक तेज़ तरीका सीखें।

उदाहरण 1: 39, 78, और 195 का HCF खोजें।

हल: चरण-दर-चरण विधि पर ध्यान दें:

• संख्याओं के बीच के अंतर पर ध्यान दें। किसी भी दो संख्याओं के बीच का अंतर लें। HCF को इन अंतरों का गुणांक होना चाहिए। अंतरे हैं: 78−39=39, 195−39=156, 195−78=117। इसलिए, HCF को 39, 156, और 117 को विभाजित करना चाहिए।
• सबसे छोटे अंतर (39) से शुरू करें। HCF को 39 का गुणांक होना चाहिए। 39 के गुणांक हैं: 1, 3, 13, और 39।
• चेक करें कि क्या सबसे बड़ा गुणांक (39) सभी संख्याओं को विभाजित करता है। क्या 39, 78 को विभाजित करता है? हाँ। क्या 39, 195 को विभाजित करता है? हाँ। इसलिए, 39, 78, और 195 का HCF 39 है।

उदाहरण 2: 39, 78, और 182 का HCF खोजें।

• संख्याओं के बीच के अंतरों को खोजें। 78−39=39, 182−39=143, 182−78=104।
• 39 के गुणांक (1, 3, 13, 39) की जाँच करें। क्या 39, 182 को विभाजित करता है? नहीं।
• अगले सबसे बड़े गुणांक, 13 को आजमाएं। क्या 13, 39 को विभाजित करता है? हाँ। क्या 13, 182 को विभाजित करता है? हाँ। इसलिए, 39, 78, और 182 का HCF 13 है।

यह विधि क्यों काम करती है?

• जब हम दो संख्याओं के बीच का अंतर खोजते हैं, तो उन संख्याओं का HCF उस अंतर का गुणांक होना चाहिए। इसका कारण यह है कि केवल वे संख्याएँ जो दोनों संख्याओं को विभाजित करती हैं, वे उनके अंतर को भी विभाजित करेंगी।
• सबसे छोटे अंतर से शुरू करके और इसके गुणांकों की जांच करके, हम बिना सभी संख्याओं के लिए लंबे विभाजन का उपयोग किए बिना जल्दी से HCF खोज सकते हैं।
• यह विधि समय बचाती है और HCF खोजना सरल बनाती है!

दो या अधिक संख्याओं का Least Common Multiple (LCM) वह सबसे छोटी संख्या है जो सभी को पूर्ण रूप से विभाजित करती है। दूसरे शब्दों में, यह दी गई संख्याओं के सभी अभाज्य गुणकों की उच्चतम शक्तियों का गुणनफल है।

दिए गए संख्याओं का LCM (Lowest Common Multiple) खोजने के लिए:

• LCM सभी गुणकों की उच्चतम शक्ति का गुणनफल होगा जो दिए गए संख्याओं में होते हैं।

चलो कुछ हल किए गए उदाहरण लेते हैं।

प्रश्न: 96, 36 और 18 का LCM खोजें।

हल:

पहले, प्रत्येक संख्या को उनके प्राइम फैक्टर्स में विभाजित करें:

• 96 = 2 x 2 x 2 x 2 x 2 x 3 = 2⁵ x 3¹
• 36 = 2 x 2 x 3 x 3 = 2² x 3²
• 18 = 2 x 3 x 3 = 2¹ x 3²

इसलिए, 96, 36 और 18 का LCM सभी प्राइम फैक्टर्स की उच्चतम शक्तियों का गुणनफल है, अर्थात्:

• 2⁵ x 3² = 32 x 9 = 288।

यानी, 288 सबसे छोटी पूर्णांक है, जो 96, 36 और 18 द्वारा बिना किसी शेष के विभाज्य है।

प्रश्न: 42 और 70 का LCM खोजें।

हल:

• 42 = 3 x 2 x 7
• 70 = 5 x 2 x 7

इसलिए, LCM है:

• 2 x 3 x 5 x 7 = 210।

प्राइम फैक्टराइजेशन की विधि के अलावा, दिए गए संख्याओं का LCM खोजने की एक और विधि है, जिसे लॉन्ग डिवीजन विधि कहा जाता है। यह विधि तीन या उससे अधिक संख्याओं के लिए LCM जल्दी प्राप्त करने में सहायक है।

डिवीजन विधि द्वारा LCM

संख्याओं को लिखें, उन्हें कॉमा द्वारा अलग करें। फिर उन्हें क्रम में प्राइम फैक्टर्स द्वारा विभाजित करें (जैसे, 2, 3, 5, 7, आदि) एक बार में। फिर, प्रत्येक विभाजन के बाद, प्रत्येक संख्या के पूर्ण विभाजित भाग (क्वोटिएंट) को उसके नीचे लिखें। जिन संख्याओं का विभाजन नहीं हुआ है, उन्हें वैसा ही छोड़ दें। यह प्रक्रिया तब तक जारी रखें जब तक प्रत्येक कॉलम में प्राइम फैक्टर्स क्वोटिएंट के रूप में न हों। सभी प्राइम फैक्टर्स (डिविजर्स और क्वोटिएंट्स) का गुणनफल LCM होगा।

प्रश्न: 8, 12, 15 और 21 का LCM ज्ञात करें।

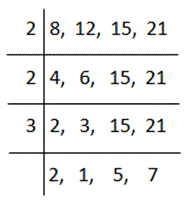
इस प्रकार, LCM है 2 × 2 × 2 × 3 × 5 × 7 = 840।

• A, B और C का HCF सबसे बड़ा भाजक है जो A, B और C को सटीक रूप से विभाजित कर सकता है।
• A, B और C का LCM सबसे छोटा भाज्य है जो A, B और C द्वारा सटीक रूप से विभाजित किया जा सकता है।

दो संख्याओं और उनके HCF और LCM के बीच एक बहुत महत्वपूर्ण संबंध है, जो नीचे दिया गया है। इस संबंध पर आधारित कई समस्याएँ विभिन्न प्रतियोगी परीक्षाओं में आई हैं।

उदाहरण: दो संख्याओं का LCM और HCF क्रमशः 2079 और 27 है। यदि इनमें से एक संख्या 189 है, तो दूसरी संख्या ज्ञात करें।

समाधान: दूसरी संख्या होगी =

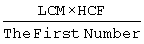
इस प्रकार, आवश्यक संख्या =

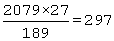
उदाहरण: दो संख्याएँ 3: 5 के अनुपात में हैं और उनका LCM 1500 है। संख्याओं का HCF ज्ञात करें।

समाधान: मान लीजिए दो संख्याएँ 3X और 5X हैं। इस प्रकार उनका HCF = X है। उपरोक्त दिए गए सूत्र का उपयोग करते हुए, हमें LCM = 3 × 5 × X = 15X मिलता है। या, 15X = 1500 => X = 100। इसलिए, संख्याओं का HCF 100 है।

भिन्नों का HCF और LCM

हम निम्नलिखित प्रत्यक्ष सूत्र का उपयोग कर सकते हैं।

भिन्नों का HCF =

इसी प्रकार, भिन्नों का LCM =

उदाहरण: दो भिन्नों 6/9, 12/15 का HCF और LCM ज्ञात करें।

समाधान: अंश 6 और 12 हैं, उनका HCF = 6 और LCM = 12 है। हर 9 और 15 का LCM = 45 और HCF = 3 है। इस प्रकार, आवश्यक HCF = और LCM = 12/3 = 4 है।

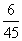
उदाहरण: एक आदमी 51 किमी और 85 किमी को सटीक संख्या में मिनटों में चलने की अधिकतम दर क्या है?

समाधान: यह ज्ञात करने के लिए कि आदमी 51 किमी और 85 किमी को सटीक संख्या में मिनटों में चलने की अधिकतम दर क्या है, हमें 51 और 85 का सबसे बड़ा सामान्य भाजक ज्ञात करना होगा। यह समस्या 51 किमी और 85 किमी की दूरी का HCF (Highest Common Factor) पूछ रही है।

चरण-दर-चरण प्रक्रिया:

1. 51 और 85 का HCF ज्ञात करें:

• 51 के प्राथमिक गुणांक हैं: 51 = 3 × 17
• 85 के प्राथमिक गुणांक हैं: 85 = 5 × 17

51 और 85 के बीच सामान्य गुणांक 17 है।

2. परिणाम: सबसे बड़ी संभव गति जिस पर व्यक्ति एक निश्चित संख्या में मिनटों में चल सकता है, वह 17 किमी प्रति मिनट है, क्योंकि 17 वह सबसे बड़ा संख्या है जो 51 और 85 दोनों को ठीक से विभाजित करता है।

इसलिए, सबसे बड़ी संभव गति 17 किलोमीटर प्रति मिनट है।

शेषफल

• हम जानते हैं कि जब एक संख्या M को दूसरी संख्या N से विभाजित किया जाता है, और यदि M > N है, तो शेषफल की गणना N के अधिकतम संभावित गुणांक को M से घटाकर की जाती है।
• इस प्रक्रिया में घटाने के बाद जो अधिशेष भाग बचता है, उसे शेषफल कहा जाता है, N का अधिकतम गुणांक को भाज्य (Quotient) कहा जाता है, और M और N को क्रमशः भाजक (Dividend) और भाजक (Divisor) कहा जाता है।
• हमारे पास उनके बीच निम्नलिखित संबंध है: भाजक = भाज्य × भाजक + शेषफल

शेषफल पर महत्वपूर्ण बिंदु

• शेषफल हमेशा भाजक से कम होता है।
• यदि शेषफल 0 है, तो भाजक को भाजक का गुणांक कहा जाता है।
• यदि भाजक भाजक से कम है, तो शेषफल स्वयं भाजक होता है।

उदाहरण: 5 को 6 से विभाजित करने पर, शेषफल केवल 5 है।

• शेषफल को हमेशा इसके वास्तविक रूप में गणना की जानी चाहिए। अर्थात्, इसे सबसे सरल रूप में नहीं घटाया जाना चाहिए।

उदाहरण: जब 4 को 6 से विभाजित किया जाता है, तो शेषफल 4 है न कि 2।

शेषफल प्रमेय

अवशिष्ट प्रमेय हमें एक संख्या द्वारा भाग देने पर अवशिष्ट (remainder) ज्ञात करने में मदद करता है, बिना पूरे गुणनफल की गणना किए। आइए इसे 17 x 23 को 12 से विभाजित करने के उदाहरण से समझते हैं।

चरण-दर-चरण व्याख्या:

• संख्याओं को फिर से लिखें: हम संख्याओं 17 और 23 को इस तरह व्यक्त कर सकते हैं कि उसमें 12 शामिल हो: 17 = 12 × 1 + 5 और 23 = 12 × 1 + 11। इसलिए, हम इस अभिव्यक्ति को फिर से लिख सकते हैं: 17 x 23 = (12 × 1 + 5) x (12 × 1 + 11)
• अभिव्यक्ति का विस्तार करें: वितरण गुण (distributive property) का उपयोग करते हुए, अभिव्यक्ति का विस्तार करें: (12 × 1 + 5)(12 × 1 + 11) = 12 × 12 + 12 × 11 + 5 × 12 + 5 × 11
• शब्दों की पहचान करें:
  • 12 × 12 (12 से विभाज्य है, इसलिए इसका अवशिष्ट 0 है)
  • 12 × 11 (12 से विभाज्य)
  • 5 × 12 (12 से विभाज्य)
  • अंतिम शब्द: 5 × 11
• अंतिम शब्द पर ध्यान दें: 12 से विभाजित करते समय केवल 5 × 11 अवशिष्ट को प्रभावित करता है। 5 × 11 = 55।
• अवशिष्ट ज्ञात करें: अब, हमें 55 को 12 से विभाजित करने पर अवशिष्ट ज्ञात करना है: 55 / 12 = 4, शेष 7।

इस प्रकार, 17 x 23 को 12 से विभाजित करने पर अवशिष्ट 7 है।

अवशिष्ट प्रमेय अवशिष्ट ज्ञात करने की प्रक्रिया को सरल बनाता है, केवल उन प्रासंगिक शब्दों पर ध्यान केंद्रित करके जो विभाजक के संदर्भ में संख्याओं को फिर से लिखने के बाद होते हैं। हमारे उदाहरण में, हमें अवशिष्ट ज्ञात करने के लिए केवल अंतिम शब्द 5×11 पर विचार करने की आवश्यकता थी।

नकारात्मक शेष का सिद्धांत

गणित में, शेष हमेशा गैर-नकारात्मक पूर्णांक होते हैं। हालांकि, हम कई प्रश्नों को आसानी से और कम गणना में हल करने के लिए नकारात्मक पूर्णांकों के सिद्धांत का उपयोग कर सकते हैं।

इसे समझने के लिए हम एक उदाहरण लेते हैं:

हमें पता है कि जब 15 को 4 से विभाजित किया जाता है, तो प्राप्त शेष 3 होता है क्योंकि 15, 4 का निकटतम गुणांक 12 से 3 अधिक है। यहां हम 15 की तुलना 12 (4 का सबसे बड़ा गुणांक जो 15 के बराबर या उससे कम है) से कर रहे हैं और पाएंगे कि 15, 12 से 3 अधिक है। इसलिए अतिरिक्त भाग 3 है, जो शेष है। यदि हम 12 की बजाय 15 की तुलना 16 (4 का एक और गुणांक जो 15 के करीब है) से करें, तो हम कह सकते हैं कि 15, 16 से 1 कम है। या 15 में 4 से विभाज्य होने के लिए 1 की कमी है। इस कमी वाले संख्या को नकारात्मक शेष कहा जाता है। अर्थात्, हम कह सकते हैं कि जब 15 को 4 से विभाजित किया जाता है, तो शेष -1 है।

नकारात्मक शेष से संबंधित सकारात्मक शेष में परिवर्तन और इसके विपरीत

• यदि N को 5 से विभाजित करने पर प्राप्त शेष -2 है, तो सकारात्मक शेष 5 - 2 = 3 होगा।
• इसी प्रकार, यदि 7 से विभाजित करते समय प्राप्त सकारात्मक शेष 4 है, तो नकारात्मक शेष 4 - 7 = -3 होगा।

हम नकारात्मक शेष के उपयोग को समझने के लिए कुछ उदाहरणों में इस सिद्धांत का उपयोग करेंगे।

नोट: किसी भी दो या अधिक संख्याओं का गुणन, योग और घटाव किसी प्राकृतिक संख्या से विभाजित करने पर वही शेष प्राप्त होता है जैसे कि उनके शेषों का गुणन, योग और घटाव।

आइए इसे एक उदाहरण के साथ समझते हैं: मान लीजिए एक संख्या N =। अब हम यह पता करते हैं कि जब N को 5 से विभाजित किया जाता है, तो शेषफल क्या होता है। एक तरीका यह है कि हम पहले N का मान निकालते हैं = अर्थात्, जो 197 के बराबर है। और फिर इस संख्या को 5 से विभाजित करके शेषफल प्राप्त करते हैं = 2।

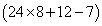
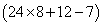
दूसरा तरीका यह है कि हम N में दिए गए प्रत्येक संख्या का शेषफल निकालते हैं, जब इसे 5 से विभाजित किया जाता है, और फिर इन शेषफलों के साथ संबंधित गणितीय ऑपरेटर का उपयोग करते हैं।

• जब 24 को 5 से विभाजित किया जाता है, तो शेषफल = 4
• जब 8 को 5 से विभाजित किया जाता है, तो शेषफल = 3
• जब 12 को 5 से विभाजित किया जाता है, तो शेषफल = 2
• जब 7 को 5 से विभाजित किया जाता है, तो शेषफल = 2

संख्याओं को उनके संबंधित शेषफलों के साथ प्रतिस्थापित करते हैं, हम पाते हैं, चूंकि 12, 5 से अधिक है, हमने 12 को फिर से 5 से विभाजित किया ताकि अंतिम शेषफल = 2 प्राप्त हो सके।

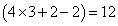
नोट: दूसरा तरीका दिए गए उदाहरण के लिए कठिन या अनावश्यक लग सकता है। लेकिन समझने के उद्देश्य से विस्तृत व्याख्यान दिए गए हैं, हम देखेंगे कि इस दूसरे तरीके को लागू करके हम उन्नत समस्याओं को कैसे हल कर सकते हैं।

ऊपर दिए गए समस्या में सकारात्मक शेषफल और नकारात्मक शेषफल के सिद्धांत को एक साथ लागू करते हुए:

• जब 24 को 5 से विभाजित किया जाता है, तो शेषफल = -1
• जब 8 को 5 से विभाजित किया जाता है, तो शेषफल = -2
• जब 12 को 5 से विभाजित किया जाता है, तो शेषफल = 2
• जब 7 को 5 से विभाजित किया जाता है, तो शेषफल = 2

संख्याओं को उनके संबंधित शेषफलों के साथ प्रतिस्थापित करते हैं, हम पाते हैं, इस प्रकार अंतिम शेषफल = 2 है।

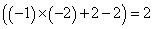
प्रश्न: 123 × 124 × 125 को 9 से विभाजित करने पर शेषफल क्या है?

समाधान: 123 को 9 से विभाजित करने पर प्राप्त शेषफल = -3
124 को 9 से विभाजित करने पर प्राप्त शेषफल = -2
123 को 9 से विभाजित करने पर प्राप्त शेषफल = -1
अंतिम शेषफल = (-3)(-2)(-1) = -6। आवश्यक सकारात्मक शेषफल = 9-6 = 3।

प्रश्न: 1! 2! 3! …. 100! को 5 से विभाजित करने पर शेषफल क्या है।

समाधान: ध्यान दें कि श्रृंखला 5! से आगे हर संख्या 5 के द्वारा विभाजित है, अर्थात् प्रत्येक मामले में शेषफल 0 है। इसलिए आवश्यक शेषफल केवल पहले 4 संख्याओं को विभाजित करके प्राप्त किया जाएगा।

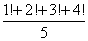
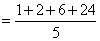
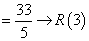
चक्रवृत्तता

1. अंक 0, 1, 5 और 6:

जब हम इन अंकों के व्यवहार का अवलोकन करते हैं, तो ये सभी किसी भी शक्ति पर उठाने पर संख्या के समान ही इकाई अंक रखते हैं, अर्थात् 0ⁿ = 0, 1ⁿ = 1, 5ⁿ = 5, 6ⁿ = 6।

• 5² = 25: इकाई अंक 5, संख्या स्वयं।
• 16¹ = 1: इकाई अंक 1, संख्या स्वयं।
• 04⁰ = 0: इकाई अंक 0, संख्या स्वयं।
• 63³ = 216: इकाई अंक 6, संख्या स्वयं।

आइए इस सिद्धांत को निम्नलिखित उदाहरण पर लागू करें।उदाहरण: निम्नलिखित संख्याओं का इकाई अंक खोजें:

• 185563 उत्तर = 5
• 52716987 उत्तर = 7
• 115625369 उत्तर = 9
• 6190654789321 उत्तर = 1
• 0 उत्तर = 0

2. अंक 4 और 9:

इन दोनों संख्याओं का चक्रवृत्तता केवल दो विभिन्न अंकों के रूप में है।

• 4² = 16: इकाई अंक 6।
• 4³ = 64: इकाई अंक 4।
• 4⁴ = 256: इकाई अंक 6।
• 4⁵ = 1024: इकाई अंक 4।
• 9² = 81: इकाई अंक 1।
• 9³ = 729: इकाई अंक 9।

यह देखा जा सकता है कि इकाई अंकों 6 और 4 का दोहराव विषम-सम क्रम में हो रहा है। इसलिए, 4 की चक्रवृत्तता 2 है। 9 के साथ भी यही स्थिति है। इसे निम्नलिखित रूप में सामान्यीकृत किया जा सकता है:

उत्तर: 189562589743 = 9 (क्योंकि घात विषम है)
279698745832 = 1 (क्योंकि घात सम है)
154258741369 = 4 (क्योंकि घात विषम है)
19465478932 = 6 (क्योंकि घात सम है)

3. अंक 2, 3, 7 और 8:

ये अंक 4 विभिन्न अंकों के घात चक्र का पालन करते हैं। 21 = 2, 22 = 4, 23 = 8 और 24 = 16 के बाद यह दोहराना शुरू होता है। इसलिए, 2 का चक्र 4 विभिन्न अंकों 2, 4, 8, 6 का है। 31 = 3, 32 = 9, 33 = 27 और 34 = 81 के बाद यह दोहराना शुरू होता है। इसलिए, 3 का चक्र 4 विभिन्न अंकों 3, 9, 7, 1 का है। 7 और 8 समान तर्क का पालन करते हैं। इसलिए ये चार अंक अर्थात् 2, 3, 7 और 8 के पास चार चरणों का एकक अंक चक्र है।

चक्रता तालिका

उपरोक्त चर्चा किए गए विचारों का सारांश निम्नलिखित तालिका में दिया गया है।

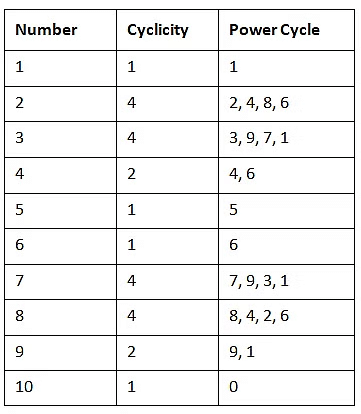
शून्य दो और पाँच के संयोग द्वारा बनते हैं। इसलिए, शून्य की संख्या उन जोड़ों की संख्या पर निर्भर करेगी जो 2 और 5 के बीच बन सकते हैं। उपरोक्त गुणनफल में, चार 2 और तीन 5 हैं। इसलिए, हम केवल तीन (2 × 5) के जोड़ बना सकेंगे। इस प्रकार, गुणनफल में 3 शून्य होंगे।

• इसलिए, शून्य की संख्या उन जोड़ों की संख्या पर निर्भर करेगी जो 2 और 5 के बीच बन सकते हैं।
• उपरोक्त गुणनफल में, चार 2 और तीन 5 हैं। इसलिए, हम केवल तीन (2 × 5) के जोड़ बना सकेंगे।

2. फैक्टोरियल मान में शून्य की संख्या पता करना

• विधि 1: मान लीजिए कि आपको 6! में शून्य की संख्या पता करनी है। 6! = 6 × 5 × 4 × 3 × 2 × 1 = (3 × 2) × (5) × (2 × 2) × (3) × (2) × (1)। 5 की संख्या गिनने से उत्तर मिल जाएगा।
• विधि 2: 6! में शून्य की संख्या पता करने के लिए हम उपयोग करते हैं। इसलिए पहले टर्म के बाद सभी विभाजनों में दशमलव होते हैं जिन्हें हम नजरअंदाज करते हैं, इसलिए हमें उत्तर 1 मिलता है।

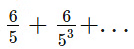
प्रश्न: 12 × 15 × 5 × 24 × 13 × 17 (क) 0 (ख) 1 (ग) 2 (घ) 3 उत्तर: (ग)

हल: 22∗3∗3∗5∗5∗23∗3∗13∗17 = इसलिए (5*2) के जोड़ 2 हैं, इसलिए हमारे पास 2 शून्य हैं।

3. एक विशेष अर्थ

• जब हम 45!, 46!, 47!, 48!, 49! का हल कर रहे हैं। हर मामले में शून्य की संख्या 10 के बराबर होगी। यह समझना मुश्किल नहीं है कि इन फैक्ट्रियल्स में 5 की संख्या 10 के बराबर है। 50! पर शून्य की संख्या केवल बदल जाएगी (यह 12 हो जाएगी)। वास्तव में, यह सभी फैक्ट्रियल मानों के लिए सच होगा जो 5 के दो लगातार उत्पादों के बीच आते हैं।
• इस प्रकार, 50!, 51!, 52!, 53! और 54! में 12 शून्य होंगे (क्योंकि इनमें सभी में 12 पाँच हैं)। इसी तरह, 55!, 56!, 57!, 58! और 59! में प्रत्येक में 13 शून्य होंगे। जबकि 49! में 10 शून्य हैं, 50! में सीधे 12 शून्य हैं। इसका मतलब है कि ऐसा कोई फैक्ट्रियल मान नहीं है जो 11 शून्य देगा। यह इस कारण होता है कि 50! प्राप्त करने के लिए हम 49! के मान को 50 से गुणा करते हैं। जब आप ऐसा करते हैं, तो उत्पाद में दो 5 का योगदान होता है। इसलिए, शून्य की संख्या दो से बढ़ जाती है।
• नोट: 124! पर आपको 24 से 28 शून्य मिलेंगे। 125! पर आपको 25 से 31 शून्य मिलेंगे। (शून्य में 3 का उछाल।)

• उदाहरण: n! में 13 शून्य हैं। n के उच्चतम और न्यूनतम मान क्या हैं? (क) 57 और 58 (ख) 59 और 55 (ग) 59 और 6 (घ) 79 और 55 उत्तर: (ख)

समाधान: 55 पर हमें 13 शून्य मिलते हैं, क्योंकि हमें पता है कि 50! में 12 शून्य हैं, इसलिए 54! तक हमें 12 शून्य मिलेंगे। इसलिए 55 से 59! तक 13 शून्य होंगे।

आधार प्रणाली

• 1. दशमलव संख्या प्रणाली (आधार- 10)
• 2. द्विआधारी संख्या प्रणाली (आधार- 2)
• 3. अष्टाधारी संख्या प्रणाली (आधार- 8)
• 4. षटाधारी संख्या प्रणाली (आधार- 16)

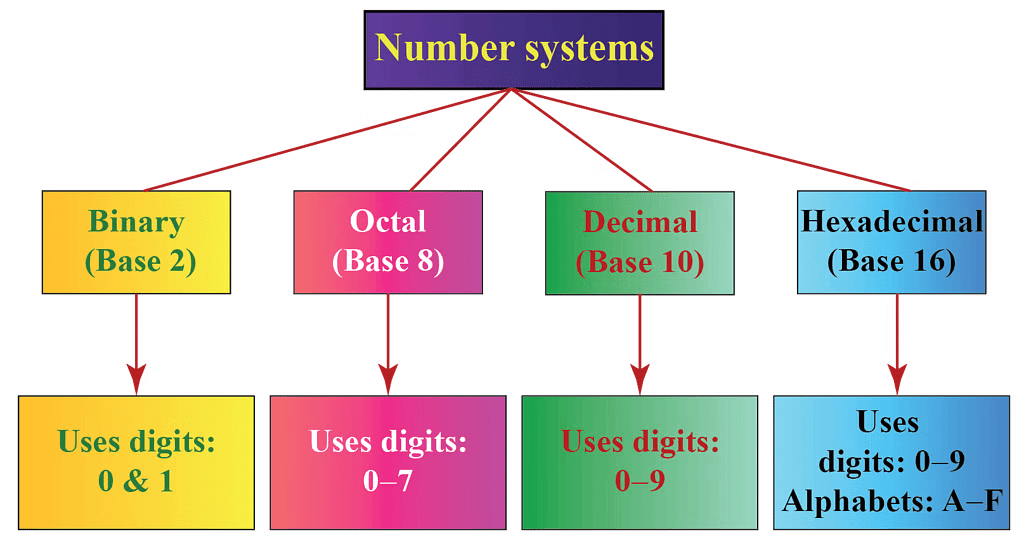
1. दशमलव संख्या प्रणाली (आधार- 10) दशमलव संख्या प्रणाली, जिसका आधार 10 है, में अंक 0 से 9 तक होते हैं। दशमलव बिंदु के बाईं ओर स्थित स्थान 10 की शक्तियों का प्रतिनिधित्व करते हैं, जो इकाइयों, दहाई, सैकड़ों आदि को इंगित करते हैं। उदाहरण: 3567.89 इस उदाहरण में, अंक 3 हजारों के स्थान पर है (10³), अंक 5 सैकड़ों के स्थान पर है (10²), अंक 6 दहाई के स्थान पर है (10¹), अंक 7 इकाइयों के स्थान पर है (10⁰ या 1), अंक 8 दशमलव के स्थान पर है और अंक 9 शतांश के स्थान पर है।

2. द्विआधारी संख्या प्रणाली (आधार- 2) द्विआधारी, या आधार-2, में केवल दो अंक होते हैं, 0 और 1। द्विआधारी संख्याएँ, जैसे कि 110101, इन दो अंकों के संयोजनों से बनी होती हैं। उदाहरण: 110101 सबसे दाएं अंक 2⁰ है, अगला 2¹ है, फिर 2² है, और इसी प्रकार। द्विआधारी संख्या 110101 दशमलव प्रणाली में (1 * 2⁵) (1 * 2⁴) (0 * 2³) (1 * 2²) (0 * 2¹) (1 * 2⁰) = 53 के बराबर है।

3. अष्टाधारी संख्या प्रणाली (आधार- 8) अष्टाधारी, जिसका आधार 8 है और अंक 0 से 7 तक होते हैं, का उपयोग कंप्यूटिंग में किया जाता है। अष्टाधारी को दशमलव में परिवर्तित करने की प्रक्रिया मानक दशमलव परिवर्तनों के समान होती है। उदाहरण: 745 उदाहरण में 745, सबसे दाएं अंक 8⁰ है, अगला 8¹ है, और सबसे बाएं अंक 8² है। इसे दशमलव में परिवर्तित करते समय, अष्टाधारी संख्या 745 (7 * 8²) (4 * 8¹) (5 * 8⁰) = 485 के बराबर होती है।

हेक्साडेसिमल (Hexadecimal) संख्या प्रणाली में आधार 16 का उपयोग होता है, जो संख्याओं को 0 से 9 तक दर्शाता है, और फिर A से F का उपयोग 10 से 15 के मानों के लिए किया जाता है। यह प्रणाली आमतौर पर कंप्यूटिंग में उपयोग की जाती है। उदाहरण: 1A3F। उदाहरण 1A3F में, यह (1 * 163) (10 * 162) (3 * 161) (15 * 160) = 6719 के बराबर है, जो दशमलव प्रणाली में है।

प्रश्न 1: 55552345 66665678 का अंतिम अंक क्या है? (a) 1 (b) 3 (c) 5 (d) 7
उत्तर: (a)

क्योंकि अंतिम अंक केवल अंतिम अंकों पर निर्भर करता है, इसलिए केवल अंतिम अंकों के लिए शक्तियों पर विचार करें, अर्थात् 52345 65678। जैसे कि हम जानते हैं, 5 की कोई भी शक्ति केवल 5 से समाप्त होती है और 6 की कोई भी शक्ति केवल 6 से समाप्त होती है। इसलिए 52345 65678 का अंतिम अंक = 5 6 = 11 = 1। इसलिए, विकल्प (A) सही उत्तर है।

प्रश्न 2: यदि एक दो अंकों के नंबर में, यूनिट स्थान पर अंक z है और टेन्स स्थान पर अंक 8 है, तो नंबर क्या है? (a) 80z z (b) 80 z (c) 8z 8 (d) 80z 1
उत्तर: (b)

यूनिट स्थान पर अंक = z
टेन्स स्थान पर अंक = 8
दो अंकों का नंबर = (10×8) (1×z) = 80 z

प्रश्न 3: 60! में कितने ट्रेलिंग ज़ीरो (अंक के अंत में ज़ीरो) हैं? (a) 14 (b) 12 (c) 10 (d) 8
उत्तर: (a)

• शुरू में, किसी संख्या के दशमलव प्रतिनिधित्व में ट्रेलिंग ज़ीरो की संख्या = उस संख्या को विभाजित करने वाली 10 की सबसे बड़ी शक्ति। उदाहरण के लिए, 3600 = 36 * 10², 45000 = 45 * 10³।
• इस प्रश्न के लिए, हमें पहले यह देखना होगा कि सबसे छोटा फैक्टोरियल जो एक ज़ीरो के साथ समाप्त होता है, वह क्या है।
• 1! = 1
  2! = 2
  3! = 6
  4! = 24
  5! = 120
• अब, 5! एक ज़ीरो के साथ समाप्त होता है क्योंकि जब हम 1 * 2 * 3 * 4 * 5 की गणना करते हैं, तो हमें 10 का गुणनफल मिलता है। 10, 2 * 5 है, इसलिए हमें 10 का एक गुणांक हर बार मिलता है जब हम फैक्टोरियल में 2 और 5 पाते हैं।
• इसलिए, 5! में 1 ज़ीरो है। 10! में 2 ज़ीरो हैं। 15! में 3 ज़ीरो हैं। 20! में 4 ज़ीरो हैं, और इसी तरह।
• एक अतिरिक्त ज़ीरो तब बनता है जब 2 और 5 मिलते हैं। हर सम संख्या एक 2 देती है, जबकि हर पाँचवीं संख्या हमें एक 5 देती है।
• अब, यहाँ महत्वपूर्ण बिंदु यह है कि चूंकि हर सम संख्या फैक्टोरियल में कम से कम एक 2 का योगदान देती है, 2 की संख्या 5 से बहुत अधिक होती है। इसलिए, किसी संख्या को विभाजित करने वाली 10 की सबसे बड़ी शक्ति खोजने के लिए, हमें केवल उस संख्या को विभाजित करने वाले 5 की सबसे बड़ी शक्ति की गणना करनी होगी।
• अब, हर 5 का गुणांक फैक्टोरियल में एक ज़ीरो जोड़ेगा। 1 * 2 * 3 *.......59 * 60 में बारह 5 के गुणांक हैं। इसलिए, ऐसा लगता है कि 60! 12 ज़ीरो के साथ समाप्त होगा।
• लेकिन हमें यहाँ एक और समायोजन करना होगा। 25 = 5², इसलिए 25 अकेले दो 5 का योगदान देगा, और इसलिए प्रणाली में दो ज़ीरो जोड़ेगा। इसी तरह, 25 का हर गुणांक एक अतिरिक्त ज़ीरो योगदान करेगा।
• इसलिए, 20! में 4 ज़ीरो हैं, 25! में 6 ज़ीरो हैं। 60! में [60/5] ज़ीरो जोड़े जाएंगे जो गुणांक के कारण हैं और अतिरिक्त [60/25] 25 और 50 की उपस्थिति के कारण। {हम [60/25] का केवल पूर्णांक भाग रखते हैं क्योंकि दशमलव भाग का कोई मूल्य नहीं है}।
• इसलिए, 60! अंत में 12 + 2 ज़ीरो = 14 ज़ीरो के साथ समाप्त होगा।

सामान्यीकरण करते हुए, यदि हम n! में 3 की सबसे बड़ी शक्ति खोजने के लिए चाहते हैं, तो यह कुछ नहीं है। n! में 7 की सबसे बड़ी शक्ति है। यदि हम किसी सम composite संख्या की बात कर रहे हैं, तो हमें इसे उसके घटक प्राइम्स में तोड़कर उस संख्या को विभाजित करने वाली सबसे बड़ी शक्ति की गणना करनी होगी।

उदाहरण के लिए, यदि हम n! में 15 के सबसे बड़े गुणांक को खोजना चाहते हैं, तो यह n! में 3 और 5 की सबसे बड़ी शक्तियों द्वारा प्रेरित होगा। ट्रेलिंग ज़ीरो के मामले की तरह, हम देख सकते हैं कि किसी भी फैक्टोरियल में निश्चित रूप से 3 की संख्या 5 से अधिक होगी। इसलिए, n! में 15 का सबसे बड़ा गुणांक बस [n/5] [n/25] [n/125] [n/625]............ है।

प्रश्न 4: (a) 42 (b) 53 (c) 1055 (d) इनमें से कोई नहीं के गुणनफल के अंत में ज़ीरो की संख्या?
उत्तर: (a)

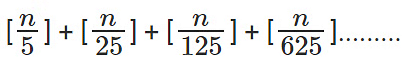
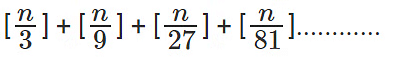
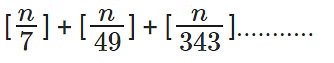
222111 × 35 53 के अंत में शून्य की संख्या 53 है। (7!)6!×(10!)5! के अंत में शून्य की संख्या 960 है। 4242×2525 के अंत में शून्य की संख्या 42 है। अतः पूरे अभिव्यक्ति के अंत में शून्य की संख्या 42 है।

प्रश्न 5: 100 ≤ n ≤ 200 के बीच कितने सम पूर्णांक n ऐसे हैं जो न तो सात से विभाजित होते हैं और न ही नौ से?

• (a) 40
• (b) 37
• (c) 39
• (d) 38

उत्तर: (c)

100 और 200 के बीच, दोनों शामिल हैं, कुल 51 सम संख्या हैं। 7 से विभाजित 7 सम संख्या हैं और 9 से विभाजित 6 संख्या हैं और 1 संख्या दोनों से विभाजित है। इसलिए कुल संख्या = 51 - (7 + 6 - 1) = 39। एक और तरीका है जिससे हम उत्तर प्राप्त कर सकते हैं। चूंकि हमें सम संख्या खोजनी हैं, 100 और 200 के बीच 14, 18 और 126 से विभाजित संख्या पर विचार करें। ये क्रमशः 7, 6 और 1 हैं।

प्रश्न 6: कितने सकारात्मक पूर्णांक (a, b) के जोड़े हैं जिनके लिए a ≤ b और ab = 42017?

• (a) 2018
• (b) 2019
• (c) 2017
• (d) 2020

उत्तर: (c)

ab = 42017 = 24034। गुणकों की कुल संख्या = 4035। इन 4035 गुणकों में से, हम दो संख्या a, b चुन सकते हैं ऐसा कि a