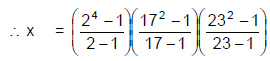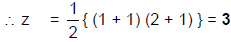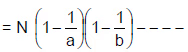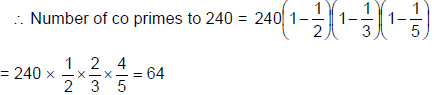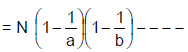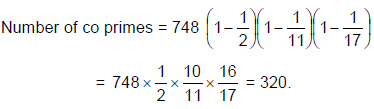चक्रीयता और गुणांक: संख्या प्रणाली | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download
चक्रीयता
- कभी-कभी ऐसे प्रश्न होते हैं जिनमें छात्रों से संख्या के घात में आने पर इकाइयों के अंक को खोजने के लिए कहा जाता है।
- यदि कोई आपसे 33 का इकाई अंक खोजने के लिए कहता है, तो आप इसे आसानी से निकाल सकते हैं, इसी तरह आप 35 के लिए भी निकाल सकते हैं, लेकिन यदि कोई आपसे 17399 का इकाई अंक पूछता है, तो इसे आसानी से निकालना कठिन होगा।
- लेकिन यह बहुत सरल है यदि हम समझें कि एक गुणनफल का इकाई अंक उस अंक के इकाई स्थान पर मौजूद अंक द्वारा निर्धारित होता है, चाहे अंकों की संख्या कितनी भी हो।
उदाहरण: 5 × 5 का परिणाम 5 पर समाप्त होता है और 625 × 625 भी 5 पर समाप्त होता है। - अब आइए देखते हैं कि एक संख्या जब अपने आप में घात में आती है तो वह कौन-से पैटर्न उत्पन्न करती है। विभिन्न संख्याओं के अंतिम अंकों को देखें।
तालिका: विभिन्न घातकों के लिए किसी संख्या का इकाई अंक दिखाना
इसलिए, किसी दिए गए संख्या के किसी भी घात का इकाई अंक निकालने के लिए, हमें निम्नलिखित चरणों का पालन करना होगा:
- चरण 1: दिए गए संख्या के घात को 4 से विभाजित करें और शेषफल की गणना करें।
- चरण 2: संख्या का इकाई अंक उसी रूप में होगा जैसे कि शेषफल की गणना की गई शक्ति में संख्या का इकाई अंक।
- चरण 3: यदि शेषफल शून्य है, तो इकाई अंक N4 के इकाई अंक के समान होगा।
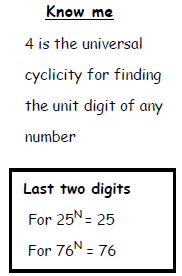
उदाहरण 1: (173)99 का अंतिम अंक ज्ञात करें।
- हम देखते हैं कि घातांक 99 है। जब 99 को 4 से विभाजित करते हैं, तो हमें 24 प्रश्नफल और 3 शेषफल मिलता है।
- अब, ये 24 जोड़े 4 के प्रत्येक के कोई प्रभाव नहीं डालते हैं। इसलिए, (173)99 ≈ (173)3
- अब, इकाई स्थान पर संख्या 33 = 27 है। इसलिए अंतिम अंक 7 है।
गुणनखंड
- गुणनखंड वह संख्या होती है जो किसी अन्य संख्या को पूरी तरह से विभाजित करती है।
उदाहरण: 24 के गुणनखंड हैं: 1, 2, 3, 4, 6, 8, 12, 24।
➢ गुणनखंडों की संख्या
- यदि हमारे पास संख्या N = pa × qb × rc है, जहाँ p, q, और r अभाज्य संख्याएँ हैं और a, b, और c प्रत्येक अभाज्य संख्या की संख्या है, तो n के गुणनखंडों की संख्या (a + 1)(b + 1)(c + 1) द्वारा ज्ञात की जाती है।
उदाहरण: 24 × 32 के गुणनखंडों की संख्या ज्ञात करें।
गुणनखंडों की संख्या = (4 + 1) (2 + 1) = (5)(3) = 15
फंडा: सभी पूर्ण वर्गों के गुणनखंडों की संख्या विषम होती है और अन्य संख्याओं के गुणनखंडों की संख्या सम होती है।
➢ किसी संख्या को दो गुणनखंडों के रूप में व्यक्त करने के तरीके
- जब किसी संख्या के गुणनखंडों की संख्या सम होती है, तो इसे दो संख्याओं के गुणनफल के रूप में व्यक्त किया जा सकता है।
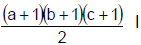
- लेकिन यदि किसी संख्या के गुणनखंडों की संख्या विषम होती है, तो इसे दो भिन्न संख्याओं के गुणनफल के रूप में व्यक्त किया जा सकता है
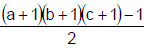 और इसे दो संख्याओं (भिन्न या समान) के गुणनफल के रूप में भी व्यक्त किया जा सकता है।
और इसे दो संख्याओं (भिन्न या समान) के गुणनफल के रूप में भी व्यक्त किया जा सकता है। 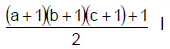
उदाहरण:
(i) 148 को 371 × 22 के रूप में व्यक्त किया जा सकता है। {इसलिए 148 के मामले में (p + 1)(q + 1)(r + 1) 6 के बराबर है, जो सम है।}
तो, दो कारकों का गुणनफल 6/2 या 3 तरीकों से किया जा सकता है।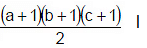
(ii) 144 को (24 . 32) के रूप में व्यक्त किया जा सकता है। {इसलिए 144 के मामले में (p + 1) (q + 1) (r + 1) 15 के बराबर है जो कि विषम है} इसे दो भिन्न संख्याओं के गुणनफल के रूप में लिखा जा सकता है, अर्थात्, 7 तरीकों से 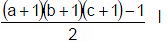
➢ किसी संख्या के गुणक का योग
- यदि कोई संख्या N को इस रूप में लिखा गया है: N = ap.bq.cr, जहाँ a, b और c अभाज्य संख्याएँ हैं और p, q और r सकारात्मक पूर्णांक हैं, तो इस संख्या के सभी गुणकों का योग निम्नलिखित सूत्र द्वारा दिया जाता है:
- गुणकों का योग =
➢ N के सह-प्रधान संख्याएँ
- N के सह-प्रधान संख्याएँ, जो N से कम हैं
फैक्टोरियल
- फैक्टोरियल किसी भी धनात्मक पूर्णांक के लिए परिभाषित किया जाता है। इसे
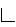 या ! द्वारा दर्शाया जाता है। इस प्रकार “फैक्टोरियल n” को n! या के रूप में लिखा जाता है
या ! द्वारा दर्शाया जाता है। इस प्रकार “फैक्टोरियल n” को n! या के रूप में लिखा जाता है 
- n! को 1 से n तक के सभी पूर्णांकों के गुणनफल के रूप में परिभाषित किया जाता है।
- इस प्रकार n! = 1.2.3. …. n. (n! = n(n – 1)!)
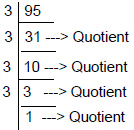
उदाहरण 2: 3 की वह सबसे बड़ी घात ज्ञात कीजिए जो 95! को बिना कोई शेष छोड़े विभाजित कर सके।
- पहले विस्तृत विवरण देखें और फिर समस्या को हल करने की सरल विधि देखें।
- जब हम 95! को उसके पूर्ण रूप में लिखते हैं, तो हमें 95 × 94 × 93 ….. × 3 × 2 × 1 प्राप्त होता है।
- जब हम 95! को 3 की घात से विभाजित करते हैं, तो हमें अंश में ये 95 संख्याएँ मिलती हैं। हर में सभी 3 होंगे। अंश में 95 संख्याओं में 3 के 31 गुणक हैं जो 3, 6, 9….90, 93 हैं। इनमें से प्रत्येक गुणन के अनुरूप हम हर में 3 प्राप्त कर सकते हैं जो अंश को बिना कोई शेष छोड़े पूरी तरह से विभाजित कर देगा, यानी 3 31 निश्चित रूप से 95! को विभाजित कर सकता है।
- इसके अलावा, 9 के प्रत्येक गुणक, यानी 9, 18, 27, आदि में ऊपर दिए गए 3 को रद्द करने के बाद भी एक और 3 बचेगा। इसलिए अंश में 9 के प्रत्येक गुणक के लिए, हमारे पास हर में एक अतिरिक्त 3 है। 95 में 9 के 10 गुणक हैं, यानी 9, 18….81, 90. इसलिए हम हर में 10 और 3 ले सकते हैं।
- इसी प्रकार, 3 के प्रत्येक गुणज के लिए हम हर में एक अतिरिक्त 3 ले सकते हैं।
- चूँकि 91 में 27 के तीन गुणज हैं (वे 27, 54 और 81 हैं), इसलिए हर में तीन और 3 हो सकते हैं।
- इसके बाद, 3 4 के प्रत्येक गुणज, यानी 81 के अनुरूप हम हर में एक और 3 रख सकते हैं। चूँकि 95 में 81 का एक गुणज है, इसलिए हम हर में एक अतिरिक्त 3 रख सकते हैं।
- अतः हर में 3 की कुल संख्या 31 + 10 + 3 + 1 है, अर्थात 45। अतः 3 45, 3 की सबसे बड़ी घात है जो 95! को बिना कोई शेष छोड़े विभाजित कर सकती है।
इसी तरह एक सरल तरीके से भी किया जा सकता है, जो नीचे समझाया गया है:
- 95 को 3 से विभाजित करने पर हमें 31 का भागफल मिलता है। इस 31 को फिर 3 से विभाजित करने पर हमें 10 का भागफल मिलता है। इस 10 को 3 से विभाजित करने पर हमें 3 का भागफल मिलता है। इस भागफल 3 को एक बार फिर 3 से विभाजित करने पर हमें 1 का भागफल मिलता है। चूंकि हम भागफल को 3 से और नहीं विभाजित कर सकते, हम यहाँ रुक जाते हैं। सभी भागफलों को जोड़ें, अर्थात् 31, 10, 3, 1 जो 45 देते हैं, जो कि 3 की सबसे बड़ी शक्ति है।
- चूंकि हम भागफल को 3 से और नहीं विभाजित कर सकते, हम यहाँ रुक जाते हैं। सभी भागफलों को जोड़ें, अर्थात् 31, 10, 3, 1 जो 45 देते हैं, जो कि 3 की सबसे बड़ी शक्ति है।
- सभी भागफलों को जोड़ें 31, 10, 3, 1, जो 45 देते हैं। {ध्यान दें कि इस प्रकार की विभाजन जहां एक चरण का भागफल अगले चरण में भागफल के रूप में लिया जाता है, इसे “सफल विभाजन” कहा जाता है। सामान्यतः, सफल विभाजन में भाजक समान नहीं होना चाहिए (जैसा कि यहाँ है)। यहाँ, संख्या 95 को लगातार 3 से विभाजित किया जा रहा है।}
टिप्पणी:
- यह विधि केवल तभी लागू होती है जब वह संख्या जिसकी सबसे बड़ी शक्ति ज्ञात की जानी है, एक प्राइम संख्या हो। यदि संख्या प्राइम संख्या नहीं है, तो हमें संख्या को सापेक्ष प्राइम के गुणनफल के रूप में लिखना होगा, प्रत्येक कारक की सबसे बड़ी शक्ति को अलग से ज्ञात करना होगा, और इन सभी सापेक्ष कारकों में से सबसे छोटी सबसे बड़ी शक्ति ही आवश्यक सबसे बड़ी शक्ति देगी।
- यह विधि केवल तभी लागू होती है जब वह संख्या जिसकी सबसे बड़ी शक्ति ज्ञात की जानी है, एक प्राइम संख्या हो।
उदाहरण 3: 200 को विभाजित करने वाली 12 की सबसे बड़ी शक्ति ज्ञात करें!
- यहाँ हम क्रमिक विभाजन विधि लागू नहीं कर सकते क्योंकि 12 एक अभाज्य संख्या नहीं है। 12 को अभाज्य गुणनखंडों के समूह में विभाजित करें।
- हम जानते हैं कि 12 को 3 × 4 के रूप में लिखा जा सकता है। इसलिए, हम 3 की सबसे बड़ी शक्ति का पता लगाएंगे जो 200! को विभाजित कर सकती है और 4 की सबसे बड़ी शक्ति जो 200! को विभाजित कर सकती है और दोनों में से कम को 12 की सबसे बड़ी शक्ति के रूप में लेंगे जो 200! को विभाजित कर सकती है।
- 4 की उच्चतम घात ज्ञात करने के लिए, चूँकि 4 स्वयं एक अभाज्य संख्या नहीं है, इसलिए हम क्रमिक विभाजन विधि को सीधे लागू नहीं कर सकते। हमें सबसे पहले 2 की उच्चतम घात ज्ञात करनी होगी जो 200 को विभाजित कर सके!
- चूँकि दो 2 को साथ लेने पर 4 प्राप्त होगा, 2 की आधी घात 4 की सबसे बड़ी घात देगी जो 200 को विभाजित कर सकती है! हम पाते हैं कि 197 2 की सबसे बड़ी घात है जो 200 को विभाजित कर सकती है! इस आंकड़े का आधा - 98 - 4 की सबसे बड़ी घात होगी जो 200 को विभाजित कर सकती है!
- चूँकि 3 और 4 की सबसे बड़ी घात जो 200! को विभाजित कर सकती है, क्रमशः 97 और 98 हैं, इसलिए दोनों में से छोटी घात, अर्थात् 97, 12 की सबसे बड़ी घात होगी जो 200! को बिना कोई शेष छोड़े विभाजित कर सकती है।
उदाहरण 4: 234 × 334 × 434 का अंतिम अंक क्या है?
- दिया गया = (24) 34
- यदि n सम है तो 4n का अंतिम अंक 6 होगा।
- उत्तर 6 है
उदाहरण 5: (270)270 का सबसे दाएं गैर-शून्य अंक क्या है?
- अभीष्ट उत्तर 7 270 का अंतिम अंक है ।
- 7 घात का अंतिम अंक प्रत्येक 4 के बाद दोहराया जाता है।
- अतः 7 270 का अंतिम अंक 7 2 = 9 का अंतिम अंक होगा ।
उदाहरण 6: 1296 के कितने गुणक हैं?
- 1296 = 4 × 324
- 1296 = 4 × 4 × 81
- 1296 = 24 × 34
- गुणांक की संख्या = (4 + 1) (4 + 1) = 25।
उदाहरण 7: यदि x, 3128 के सभी गुणनखंडों का योग है और y, x के गुणनखंडों की संख्या है तथा z, दो संख्याओं के गुणनफल के रूप में 'y' लिखने के तरीकों की संख्या है, तो z =?
- 3128 = 4 × 782
- 3128 = 4 × 2 × 391
- 3128 = 2 3 × 17 × 23
- एक्स = 15 × (17 + 1) (23 + 1)
- एक्स = 3 × 5 × 9 × 2 × 8 × 3
- एक्स = 2 4 × 3 4 × 5
- ∴ y = (4 + 1) (4 + 1) (1 + 1)
- वाई = 2 × 5 2
उदाहरण 8: 240 के लिए कितने सह-प्राइम हैं, जो 240 से कम हैं?
- 240 = 16 × 15
- 240 = 2 4 × 3 × 5
- N के सह अभाज्य संख्याओं की संख्या, जो N से कम हैं
- यदि N = a p × b q × - - - - (a, b, - - - - अभाज्य संख्याएँ हैं)
उदाहरण 9: 748 के सभी सह-प्राइम का योग क्या है? जो N से कम हैं?
- 748 = 4 × 187
748 = 2 2 × 11 × 17- N के सह अभाज्य संख्याओं की संख्या, जो N से कम हैं
- N के सभी सह अभाज्य संख्याओं का योग जो N से कम हैं, N/2 है (N के सभी सह अभाज्य संख्याओं की संख्या जो N से कम हैं।
- योग = 748/2 * 320 = 119680
उदाहरण 10: 5544 को 2 सह-प्राइम के गुणन के रूप में कितने तरीकों से लिखा जा सकता है?
- यदि N = a p × b q × - - - -, जहाँ a, b, - - - - अभाज्य संख्याएँ हैं
- N को दो सह अभाज्य संख्याओं के गुणनफल के रूप में 2 n-1 तरीकों से लिखा जा सकता है, जहाँ n, N के अभाज्य गुणनखंडों की संख्या है।
- ∴ 5544 = 11 × 504
= 11 × 9 × 56
= 11 × 9 × 8 × 7
= 2 3 × 3 2 × 7 × 11
N को सह-अभाज्य संख्याओं के गुणनफल के रूप में लिखने के तरीकों की संख्या = 2 n-1
- ∴ उत्तर = 2 4-1 = 2 3 = 8. (क्योंकि, 2, 3, 7 और 11 चार अलग-अलग अभाज्य गुणनखंड हैं)।
➢ घातांक के अंतिम दो अंकों को दस सेकंड में गुणा करना
- अपने दिमाग में संख्याओं को गुणा करने के लिए इस ट्रिक और शॉर्टकट विधि का पालन करें। यह उन लोगों के लिए बहुत बड़ा लाभ हो सकता है जो CAT परीक्षा या किसी अन्य MBA प्रवेश परीक्षा की तैयारी कर रहे हैं।
- इस वीडियो में इस्तेमाल की गई ट्रिक्स सरल और सीधी हैं। शॉर्टकट सीखने के बाद आपको इस तरह के सवाल हल करने के लिए कागज़ और कलम की ज़रूरत नहीं पड़ेगी।
- किसी संख्या का अंतिम अंक: a n
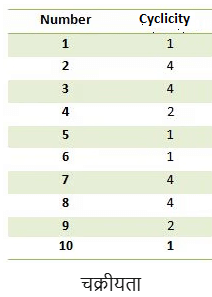
अंतिम अंक जानने के लिए अपनाई जाने वाली सरल तरकीब यह है कि दी गई संख्या के अंतिम अंक की चक्रीयता को याद रखें। घातांकीय घात लागू होने पर 1 से 9 तक प्रत्येक अंक एक पैटर्न का अनुसरण करते हैं। यहाँ एक तालिका दी गई है जो इस प्रकार के प्रश्नों को हल करने में उपयोगी होगी।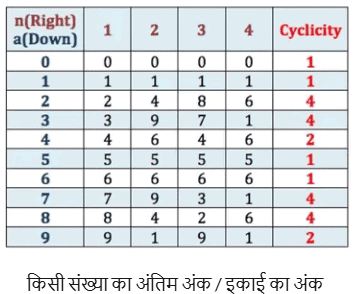
|
142 videos|172 docs|185 tests
|
FAQs on चक्रीयता और गुणांक: संख्या प्रणाली - Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA
| 1. चक्रीयता क्या है और यह संख्या प्रणाली में कैसे महत्वपूर्ण है? |  |
| 2. गुणांक क्या होता है और इसे कैसे निर्धारित किया जाता है? |  |
| 3. संख्या प्रणाली में चक्रीयता और गुणांक का उपयोग कैसे किया जाता है? |  |
| 4. क्या चक्रीयता और गुणांक के बीच कोई संबंध है? |  |
| 5. क्या चक्रीयता और गुणांक का अध्ययन केवल उच्च स्तर की गणितीय समस्याओं के लिए ही है? |  |