परिचय: सरलता और अनुमानितता | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download
परिचय
- विभिन्न प्रतियोगी परीक्षाओं के मात्रात्मक योग्यता अनुभाग में सरलीकरण, संख्या श्रृंखला, क्रमचय और संयोजन, द्विघात समीकरण, डेटा व्याख्या, डेटा विश्लेषण और अन्य विविध प्रश्न शामिल होते हैं।
- पेपर में लगभग 10 से 12 प्रश्न होते हैं जो प्रतिशत और औसत, अनुपात और समानुपात, साझेदारी, लाभ और हानि, साधारण और चक्रवृद्धि ब्याज की गणना आदि जैसे विषयों से संबंधित होते हैं।
यहाँ "सरलीकरण और अनुमान" पर प्रश्न हल करने में आपकी मदद के लिए एक संक्षिप्त अध्ययन गाइड है।
सरलीकरण के मूल नियम
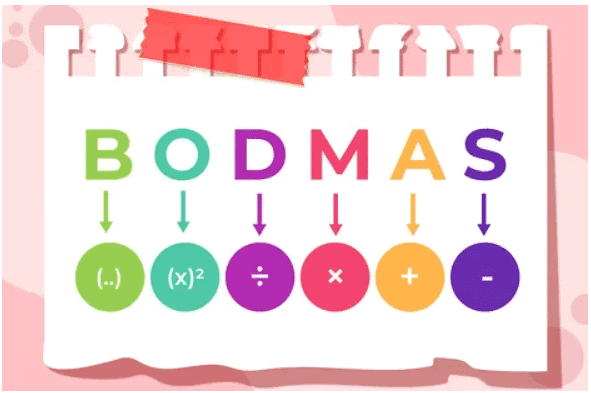
BODMAS नियम
- यह एक दिए गए गणितीय अभिव्यक्ति में सही क्रम को परिभाषित करता है जिसमें संचालन किए जाने चाहिए ताकि सही मान प्राप्त किया जा सके। इसका मतलब है कि एक अभिव्यक्ति को सरल बनाने के लिए निम्नलिखित क्रम का पालन किया जाना चाहिए -
- यह एक दिए गए गणितीय अभिव्यक्ति में सही क्रम को परिभाषित करता है जिसमें संचालन किए जाने चाहिए ताकि सही मान प्राप्त किया जा सके।
B = कोष्ठक (Bracket),
O = क्रम (Order) (शक्ति, वर्गमूल, आदि),
D = भाग (Division)
M = गुणा
A = जोड़
S = घटाव
- इसलिए, सरलन प्रश्नों को सही तरीके से हल करने के लिए, आपको सबसे पहले कोष्ठकों के संचालन को लागू करना होगा।
- इसके अलावा, कोष्ठकों को हल करते समय, क्रम - (), {} और [] - का सख्ती से पालन किया जाना चाहिए।
- इसके बाद, आपको घातांक (जैसे कि शक्तियाँ, जड़ें आदि) का मूल्यांकन करना चाहिए।
- अगला, आपको भाग और गुणा करना चाहिए, बाएं से दाएं काम करते हुए। (भाग और गुणा समान स्तर पर होते हैं और बाएं से दाएं किए जाते हैं।)
- अंततः, आपको जोड़ और घटाव करना चाहिए, बाएं से दाएं काम करते हुए। (जोड़ और घटाव समान स्तर पर होते हैं और बाएं से दाएं किए जाते हैं।)
उदाहरण 1: हल करें 12 22 ÷ 11 × (18 ÷ 3)^2 - 10
हल:
= 12 22 ÷ 11 × 6^2 - 10 (पहले कोष्ठक)
= 12 22 ÷ 11 × 36 - 10 (घातांक)
= 12 2 × 36 - 10 = 12 + 72 - 10 (भाग और गुणा, बाएं से दाएं)
= 84 - 10 = 74 (जोड़ और घटाव, बाएं से दाएं)
उदाहरण 2: हल करें 4 + 10 - 3 × 6 / 3 + 4
हल:
= 4 + 10 - 18/3 + 4 = 4 + 10 - 6 + 4 (भाग और गुणा, बाएं से दाएं)
= 14 - 6 + 4 = 8 + 4 = 12 (जोड़ और घटाव, बाएं से दाएं)

वास्तविक संख्या का माप हल करना
- माप (या परम मान) x का हमेशा या तो सकारात्मक या शून्य होता है, लेकिन कभी नकारात्मक नहीं होता।
- किसी भी वास्तविक संख्या x के लिए, x का परम मान या माप को |x| से दर्शाया जाता है और इसे इस प्रकार परिभाषित किया जाता है:
|x| = x {यदि x ≥ 0} और − x {यदि x < 0}
उदाहरण: हल करें |8|
समाधान: |8| = |-8| = 8
अनुमान लगाने के लिए सुझाव
दशमलव संख्याओं को निकटतम संख्या में परिवर्तित करना
- ऐसे प्रश्नों को हल करने के लिए, पहले दशमलव को निकटतम मान में परिवर्तित करें।
- फिर नए प्राप्त मानों का उपयोग करके दिए गए समीकरण को सरल बनाएं।
उदाहरण 1: हल करें 4433.764 - 2211.993 - 1133.667 3377.442
समाधान: यहाँ,
4433.764 = 4434
2211.993 = 2212
1133.667 = 1134
3377.442 = 3377
अब सरल बनाएं, 4434 - 2212 - 1134 + 3377 = 4466
उदाहरण 2: हल करें 530 x 20.3% 225 x 16.8%
समाधान:
यहाँ, 20.3% 20% हो जाता है और 16.8% 17% हो जाता है।
अब, सरल बनाएं 530 x 20% + 225 x 17%
= 106 + 38.25 = 144.25
वर्गमूल का अनुमान
- वर्गमूल को सरल बनाने के लिए, आप निम्नलिखित चरणों का पालन कर सकते हैं:
- वर्गमूल चिन्ह के अंदर संख्या को गुणा करें।
- यदि कोई गुणांक दो बार आता है, तो दोनों को काट दें और गुणांक को एक बार वर्गमूल चिन्ह के बाएं लिखें।
- यदि गुणांक तीन बार आता है, तो दो गुणांक को काट दें और गुणांक को चिन्ह के बाहर लिखें, और तीसरे गुणांक को चिन्ह के अंदर छोड़ दें।
- नोट: यदि कोई गुणांक 4, 6, 8, आदि बार आता है, तो इसे क्रमशः 2, 3, और 4 जोड़ियों के रूप में गिना जाता है।
- साइन के बाहर के संख्याओं को गुणा करें।
- साइन के अंदर बची संख्या को गुणा करें।
- भिन्न के वर्गमूल को सरल बनाने के लिए, अंश को सरल करें और हर को सरल करें।
नोट: यह जांचें कि बाहर की संख्या के वर्ग का गुणनफल भीतर की संख्या के बराबर होना चाहिए जो वर्गमूल के अंदर है।
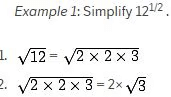

निम्नलिखित कुछ हल किए गए उदाहरण हैं जो आपको आगामी परीक्षाओं की तैयारी में मदद करेंगे:
प्रश्न 1. एक व्यक्ति के पास एक-रुपए, पांच-रुपए, और दस-रुपए के नोटों में Rs. 480 हैं। प्रत्येक संप्रदाय के नोटों की संख्या समान है। उसके पास कुल कितने नोट हैं?
A. 45
B. 60
C. 75
D. 90
उत्तर: विकल्प D
व्याख्या:
मान लीजिए कि प्रत्येक संप्रदाय के नोटों की संख्या x है।
तो, x + 5x + 10x = 480
⇒ 16x = 480
इसलिए, x = 30.
इसलिए, कुल नोटों की संख्या = 3x = 90.
प्रश्न 2. दो परीक्षा कक्ष हैं A और B। यदि 10 छात्र A से B में भेजे जाएं, तो प्रत्येक कक्ष में छात्रों की संख्या समान हो जाती है। यदि 20 उम्मीदवार B से A में भेजे जाएं, तो A में छात्रों की संख्या B की संख्या का दो गुना है। कक्ष A में छात्रों की संख्या है:
A. 20
B. 80
C. 100
D. 200
उत्तर: विकल्प C
मान लीजिए कि कक्ष A और B में छात्रों की संख्या क्रमशः x और y है।
तो, x - 10 = y और x - y = 20 .... (i)
और x + 20 = 2(y - 20)
⇒ x - 2y = -60 .... (ii)
(i) और (ii) को हल करने पर हमें मिलता है: x = 100, y = 80.
इसलिए, आवश्यक उत्तर A = 100.
प्रश्न 3. 10 कुर्सियों की कीमत 4 मेजों की कीमत के बराबर है। 15 कुर्सियों और 2 मेजों की कुल कीमत Rs. 4000 है। 12 कुर्सियों और 3 मेजों की कुल कीमत क्या होगी?
A. Rs. 3500
B. Rs. 3750
C. Rs. 3840
D. Rs. 3900
उत्तर: विकल्प D
मान लीजिए कि एक कुर्सी की कीमत Rs. x और एक मेज की कीमत Rs. y है।
तो, 10x = 4y या y = 5/2 x.
इसलिए, 15x + 2y = 4000
⇒ 15x 2*(5/2)x = 4000
⇒ 20x = 4000
इसलिए, x = 200.
तो, y = (5/2) * 200 = 500।
इस प्रकार, 12 कुर्सियों और 3 मेजों की लागत = 12x + 3y
= रुपये (2400 + 1500)
= रुपये 3900.
प्रश्न 4. यदि a - b = 3 और a2 - b2 = 29, तो ab का मान ज्ञात करें।
A. 10
B. 12
C. 15
D. 18
उत्तर: विकल्प A
2ab = (a2 - b2) - (a - b)2
= 29 - 9 = 20
⇒ ab = 10.
प्रश्न 5. 2 साड़ी और 4 शर्ट की कीमत रुपये 1600 है। उसी धन से कोई 1 साड़ी और 6 शर्ट खरीद सकता है। यदि कोई 12 शर्ट खरीदना चाहता है, तो उसे कितना भुगतान करना होगा?
A. रुपये 1200
B. रुपये 2400
C. रुपये 4800
D. निर्धारित नहीं किया जा सकता
E. इनमें से कोई नहीं
उत्तर: विकल्प B
स्पष्टीकरण:
माना एक साड़ी और एक शर्ट का मूल्य क्रमशः x रुपये और y रुपये है।
तब, 2x + 4y = 1600 .... (i)
और x + 6y = 1600 .... (ii)
समीकरण (i) को 2 से भाग देने पर हमें निम्न समीकरण प्राप्त होता है।
⇒ x + 2y = 800. --- (iii)
अब (ii) में से (iii) घटाएँ
x + 6y = 1600 (-)
x + 2y = 800
----------------
4y = 800
----------------
इसलिए, y = 200.
अब (iii) में y का मान लागू करें
⇒ एक्स + 2 एक्स 200 = 800
⇒ एक्स + 400 = 800
इसलिए x = 400
(i) और (ii) को हल करने पर हमें x = 400, y = 200 प्राप्त होता है।
अतः 12 शर्ट का मूल्य = रु. (12 x 200) = रु. 2400.
उदाहरण 6: 64 × 99
हल: ⇒ चरण 1: 64 – 1 = 63
⇒ चरण 2: 64 का पूरक = 100 – 64 = 36
उत्तर: 6336।
उदाहरण 7: 678 × 999 = ?
हल :
⇒ चरण 1: 678 – 1 = 677
⇒ चरण 2: 678 का पूरक = 1000 – 678 = 322
उत्तर: 677322।
उदाहरण 8: 78 × 999 = ?
समाधान 8: 78 को 078 के रूप में लें और सामान्य तरीके से हल करें।
⇒ स्टेप 1: 078 – 1 = 077
⇒ स्टेप 2: 078 का कॉम्प्लिमेंट = 1000 – 078 = 922
उत्तर: 77922
उदाहरण 9: संख्या 988 का वर्ग?
समाधान 9: 988 के लिए निकटतम सबसे अच्छा = 1000.988, 100 से 12 कम है
⇒स्टेप 1: 988 से 12 घटाएं = 988 – 12 = 976.
⇒ स्टेप 2: 12 का वर्ग = 144 (अंक की संख्या आधार में शून्यों की संख्या के बराबर होनी चाहिए)
उत्तर: 976144
उदाहरण 10: संख्या 102 का वर्ग?
समाधान: 102 के लिए निकटतम सबसे अच्छा = 100.102, 100 से 2 अधिक है
⇒ स्टेप 1: 102 में 2 जोड़ें = 102 + 2 = 104.
⇒ स्टेप 2: 2 का वर्ग = 04 (अंक की संख्या आधार में शून्यों की संख्या के बराबर होनी चाहिए)
उत्तर: 10404.
|
142 videos|172 docs|185 tests
|
FAQs on परिचय: सरलता और अनुमानितता - Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA
| 1. सरलता और अनुमानितता का अर्थ क्या है? |  |
| 2. सरलता और अनुमानितता का जीवन में क्या महत्व है? |  |
| 3. कैसे हम अपनी सोच में सरलता और अनुमानितता ला सकते हैं? |  |
| 4. सरलता और अनुमानितता का उपयोग किस प्रकार की समस्याओं को हल करने में किया जा सकता है? |  |
| 5. क्या सरलता और अनुमानितता एक दूसरे से जुड़े हुए हैं? |  |
















