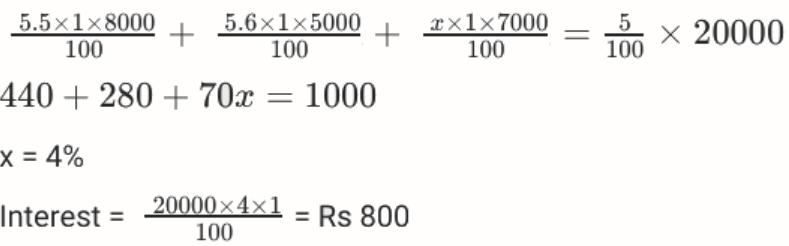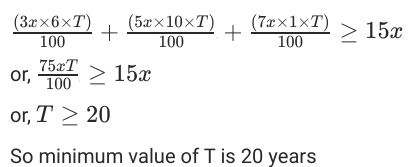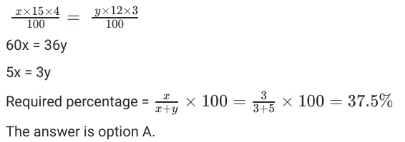बुनियादी अवधारणाएँ: साधारण ब्याज और चक्रवृद्धि ब्याज | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download
| Table of contents |

|
| ब्याज दरें क्या हैं? |

|
| संजीवनी ब्याज |

|
| संयोजित ब्याज पर हल किए गए उदाहरण |

|
| मूल्य का मूल्यह्रास |

|
| जनसंख्या आधारित प्रश्न |

|
ब्याज दरें क्या हैं?
- ब्याज दरें बहुत शक्तिशाली और आकर्षक गणितीय अवधारणाएँ हैं। हमारा बैंकिंग और वित्त क्षेत्र ब्याज दरों के आसपास घूमता है। इन दरों में एक छोटा सा परिवर्तन अर्थव्यवस्था पर विशाल और आश्चर्यजनक प्रभाव डाल सकता है। लेकिन क्यों?
- इस क्यों का कारण जानने से पहले, चलिए जानते हैं कि ब्याज और ये ब्याज दरें क्या हैं?
ब्याज वह राशि है जो उधारदाता उधारकर्ता से मुख्य ऋण राशि पर चार्ज करता है। यह मूलतः पैसे को किराए पर लेने की लागत है। और, जिस दर पर ब्याज मुख्य राशि पर चार्ज किया जाता है, उसे ब्याज दर कहा जाता है।
जिस दर पर ब्याज चार्ज किया जाता है, वह दो कारकों पर निर्भर करती है:
- पैसे का मूल्य समय के साथ समान नहीं रहता। यह समय के साथ बदलता है। आज ₹ 100 की कुल संपत्ति कल समान नहीं होगी। उदाहरण के लिए, यदि वर्तमान में ₹ 100 के नोट से 5 पेन खरीदे जा सकते हैं, तो भविष्य में शायद उसी ₹ 100 के नोट से केवल 4 पेन खरीदे जा सकें। इसके पीछे का कारण है महंगाई या कीमतों में वृद्धि। इसलिए, ब्याज दर में महंगाई का यह कारक शामिल होता है।
- उधारकर्ता की विश्वसनीयता, यदि उधारकर्ता के पक्ष में अधिक जोखिम और चूक की संभावना है, तो अधिक ब्याज लिया जाएगा। और, यदि उधारकर्ता की भुगतान विफलता की संभावना कम है, तो ब्याज की दर कम होगी।
चूंकि ब्याज दर में परिवर्तन का बाजार में श्रृंखलाबद्ध प्रभाव होता है, इसलिए यह बाजार, वित्त, और अर्थव्यवस्था के अध्ययन में बहुत महत्वपूर्ण है। और इसी कारण से, यह MBA कार्यक्रमों के पाठ्यक्रम का एक अभिन्न हिस्सा बनाता है।
ब्याज दरों के प्रकार
ब्याज के दो प्रकार होते हैं:
- सरल ब्याज
- संयुक्त ब्याज

सरल ब्याज
सरल ब्याज वह ब्याज है जो मूल राशि पर पूरे समय के लिए, एक निश्चित ब्याज दर का उपयोग करके, गणना की जाती है।
- सरल ब्याज, एक बार क्रेडिट होने के बाद, अपने आप पर ब्याज नहीं कमाता। यह समय के साथ स्थिर रहता है।
- सरल ब्याज की गणना करने का सूत्र है:
SI = {(P x R x T)/ 100}
जहां,
- P = प्रधान राशि (मूल ऋण)
- R = ब्याज की दर (जिस पर ऋण लिया जाता है)
- T = समय अवधि (जिस अवधि के लिए पैसा उधार लिया जाता है)
तो, यदि P राशि को ब्याज की दर R पर T वर्षों के लिए उधार लिया जाता है, तो उधारदाता को चुकाने के लिए राशि होगी A = P + S.I,
जहां S.I = सरल ब्याज है
और A वह राशि है जो T वर्षों के अंत में चुकाई जानी है, और यह प्रधान और ब्याज की दर का योग है।
उपरोक्त सूत्र के अनुप्रयोग को समझने के लिए एक साधारण उदाहरण पर विचार करें:
उदाहरण: ₹68000 पर 20% प्रति वर्ष के लिए 2 वर्षों का सरल ब्याज निकालें।
- यहां, P = ₹68000
- R = 20%
- T = 2 वर्ष
- S.I = (68000 x 20 x 2)/100 = ₹13600
सरल ब्याज पर आधारित उपयोगी परिणाम
नीचे दी गई तालिका में साधारण ब्याज पर कुछ उपयोगी परिणाम और उनके अनुप्रयोग दिखाए गए हैं:


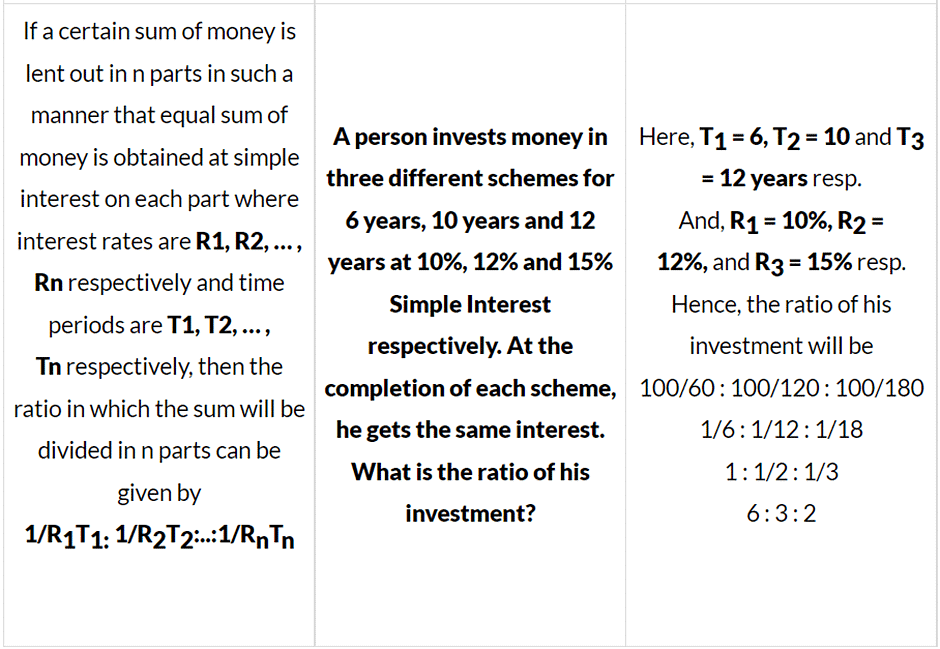
साधारण ब्याज पर हल किए गए उदाहरण
प्रश्न 1: नीतु के पास ₹20,000 की प्रारंभिक पूंजी है। इसमें से, वह बैंक A में 5.5% पर ₹8,000, बैंक B में 5.6% पर ₹5,000 और शेष राशि बैंक C में x% पर निवेश करती है, प्रत्येक दर साधारण ब्याज प्रति वर्ष है। इन निवेशों से उनकी संयुक्त वार्षिक ब्याज आय प्रारंभिक पूंजी का 5% के बराबर है। यदि उसने अपनी पूरी प्रारंभिक पूंजी केवल बैंक C में निवेश की होती, तो उसकी वार्षिक ब्याज आय, रुपये में, होती:
a. 700
b. 800
c. 900
d. 1000
हल: विकल्प 'b' सही है।
विवरण: यह दिया गया है
प्रश्न 2: श्री पिंटो अपनी पूंजी का एक-पांचवां हिस्सा 6% पर, एक-तीसवां हिस्सा 10% पर और शेष 1% पर निवेश करते हैं, प्रत्येक दर साधारण ब्याज प्रति वर्ष है। फिर, इन निवेशों से प्राप्त संचयी ब्याज आय का उनके प्रारंभिक पूंजी के बराबर या उससे अधिक होने के लिए आवश्यक न्यूनतम वर्षों की संख्या ____________ है।
हल: मान लीजिए कि कुल निवेश 15x है और आवश्यक वर्षों की संख्या T वर्ष है
प्रश्न 3: एलेक्स ने अपनी बचत को दो भागों में निवेश किया। पहले भाग पर 15% प्रति वर्ष के लिए 4 वर्षों में अर्जित साधारण ब्याज दूसरे भाग पर 12% प्रति वर्ष के लिए 3 वर्षों में अर्जित साधारण ब्याज के बराबर है। फिर, पहले भाग में निवेशित उसकी बचत का प्रतिशत है:
a. 37.5%
b. 62.5%
c. 60%
d. 40%
हल: विकल्प 'b' सही है।
विवरण: मान लीजिए कि पहले भाग में निवेशित बचत 'x' और दूसरे भाग में 'y' है। यह दिया गया है,
यह दिया गया है,
संजीवनी ब्याज
- संजीवनी ब्याज आमतौर पर बैंकिंग प्रणाली और अर्थशास्त्र में प्रयुक्त होने वाला ब्याज का सबसे सामान्य प्रकार है। इस प्रकार के ब्याज में मूलधन के साथ-साथ एक समय अवधि के पूरा होने के बाद उस पर और ब्याज अर्जित होता है।
- मान लीजिए कि राशि P को एक खाते में जमा किया गया है या उसे उधारकर्ता को उधार दिया गया है जो R% प्रति वर्ष की दर पर संजीवनी ब्याज देता है। फिर n वर्षों के बाद, जमा या ऋण इस प्रकार बढ़ेगा: P(1 + R/100)n
- उदाहरण के लिए, यदि 100 रुपये को 3 वर्षों के लिए 6% प्रति वर्ष की ब्याज दर पर बचत बैंक खाते में जमा किया जाता है।
- तब, एक वर्ष के बाद ₹100 का कुल बढ़कर ₹106 हो जाएगा। चूंकि संजीवनी ब्याज में, ब्याज स्वयं ब्याज अर्जित करता है, इसलिए दूसरे वर्ष के लिए ब्याज ₹106 पर गणना की जाएगी, जबकि साधारण ब्याज में ब्याज केवल ₹100 पर ही गणना की जाती है।
- इस प्रकार, तीसरे वर्ष के अंत के बाद कुल राशि ₹100(1.06)3 = ₹119.1016 हो जाएगी।
संजीवनी ब्याज किस्तें मान लीजिए कि एक व्यक्ति बैंक से r% पर ऋण लेता है और n वर्षों में समान किस्तों में ऋण चुकाने पर सहमति व्यक्त करता है। तब प्रत्येक किस्त का मूल्य इस प्रकार दिया गया है:
पी = एक्स/ (1 + आर/100) एन ………एक्स/ (1 + आर/100) 2 + एक्स/ (1 + आर/100)
उदाहरण: कोई व्यक्ति हाउस बिल्डिंग सोसाइटी से ₹55000 में या इस शर्त पर फ्लैट खरीद सकता है कि उसे ₹4275 नकद अग्रिम भुगतान के रूप में और शेष राशि तीन बराबर किस्तों में देनी होगी। सोसाइटी अर्ध-वार्षिक रूप से संयोजित 16% प्रति वर्ष की दर से ब्याज लेती है। यदि फ्लैट किस्त योजना के तहत खरीदा गया है, तो प्रत्येक किस्त का मूल्य ज्ञात करें।
हल: फ्लैट की कीमत ₹55000 है। अब, यदि व्यक्ति या तो ₹55000 देकर या किश्तों में फ्लैट खरीद सकता है।
चूँकि फ्लैट किश्तों में खरीदा गया था, इसलिए ऋण राशि = ₹55000 - 4275 (डाउन पेमेंट) = ₹50725।यहाँ r = 16%, 3 बराबर किस्तों में अर्धवार्षिक रूप से संयोजित।
मान लीजिए x किस्त की राशि है।तो, ₹50725 = x/ (1 + 16/200) 3 + x/ (1 + 16/200) 2 + x/ (1 + 16/200)
₹50725 = x (1/1.2591 + 1/1.1664 + 1/1.08)
₹50725 = x (0.79421 + 0.85722 + 0.9259)
₹50725 = x (2.577)
₹50725/2.5777 = xx = ₹19683
महत्वपूर्ण सूत्र
- जब ब्याज वार्षिक रूप से संयोजित होता है:
राशि = P (1 + R/100) n - जब ब्याज अर्धवार्षिक रूप से संयोजित होता है:
राशि = P (1 + (R/2)/100) 2n - जब ब्याज त्रैमासिक रूप से संयोजित होता है:
राशि = P (1 + (R/4)/100) 4n - जब अलग-अलग वर्षों के लिए दरें अलग-अलग हों, जैसे कि 1 वर्ष, 2 वर्ष और 3 वर्ष के लिए क्रमशः R 1 %, R 2 % और R 3
%। तब, राशि = P (1 + R 1 /100) (1 + R 2 /100) (1 + R 3 /100) - n वर्ष बाद देय ₹ x का वर्तमान मूल्य इस प्रकार है:
वर्तमान मूल्य = x/ (1 + R/100) n - यदि कोई निश्चित राशि n वर्षों में “ x ” गुना हो जाती है , तो चक्रवृद्धि ब्याज की दर R = 100(x 1/n – 1) होगी
- यदि कोई धनराशि P, T वर्षों के बाद चक्रवृद्धि ब्याज पर A 1 हो जाती है और वही धनराशि (T + 1) वर्षों के बाद चक्रवृद्धि ब्याज पर A 2
हो जाती है, तो R = (A 2 – A 1 )/ A 1 x 100
संयोजित ब्याज पर हल किए गए उदाहरण
उदाहरण 1: एक व्यक्ति ₹5000 का निवेश 3 वर्षों के लिए 5% प्रति वर्ष चक्रवृद्धि ब्याज पर करता है। हर वर्ष के अंत में अर्जित ब्याज पर 20% की दर से आयकर काटा जाता है। तीसरे वर्ष के अंत में राशि ज्ञात करें।
हल: यहाँ, P = ₹5000, T = 3 वर्ष, r = 5%। इसलिए,
पहले वर्ष के अंत में ब्याज = 5000 (1 + 0.05) – 5000 = ₹250अब आयकर अर्जित ब्याज पर 20% है, इसलिए आयकर काटने के बाद शेष ब्याज = (1 – 0.2) * 250 = ₹200
पहले वर्ष के अंत में कुल राशि = ₹5000 + 200 = ₹5200दूसरे वर्ष के अंत में ब्याज = 5200 (1 + 0.05) – 5200 = ₹260.
आयकर के बाद ब्याज = 0.8 * ₹260 = ₹208.
दूसरे वर्ष के अंत में कुल राशि = ₹5200 + 208 = ₹5408तीसरे वर्ष के अंत में ब्याज = ₹5408 (1.05) – 5408 = ₹270.4
आयकर के बाद ब्याज = 0.8 * ₹270.4 = ₹216.32
तीसरे वर्ष के अंत में कुल राशि = ₹5408 + 216.32 = ₹5624.32
उदाहरण 2: ₹12000 की एक राशि चक्रवृद्धि ब्याज पर 5 वर्षों में दो गुनी हो जाती है। 20 वर्षों के बाद यह कितनी हो जाएगी?
हल: मूलधन, P = 12000 रुपये;
ब्याज दर = r%;
वर्षों की संख्या, n = 5;
राशि, A = रुपये (2 × 12000) = 24000 रुपये
प्रश्न के अनुसार,
24000 = 12000 × (1 + r/100)5
⇒ (1 + r/100)5 = 2 ...(i)
अगले भाग के लिए,
मूलधन, P = 12000 रुपये;
ब्याज की दर = r%;
वर्षों की संख्या, n = 20;
राशि = x रुपये
प्रश्न के अनुसार,
x = 12000 × (1 + r/100) 20
⇒ x = 12000 × (1 + r/100) 5 × 4
⇒ x = 12000 × [(1 + r/100) 5 ] 4
⇒ x = 12000 × 2 4 ...[(i) से]
⇒ x = 192000
∴ 20 वर्ष बाद यह 1,92,000 रुपये हो जाएगाशॉर्टकट ट्रिक
12000 5 साल में दोगुना हो जाता है = 12000 × 2 = 24000
अन्य 5 साल बाद = 24000 × 2 = 48000
अन्य 5 साल बाद = 48000 × 2 = 96000
अन्य 5 साल बाद = 48000 × = 1,92,000
∴ 20 साल बाद योग होगा = 192000
उदाहरण 3: जॉन ने एक बैंक से 2,10,000 रुपये उधार लिए, जिन पर 10% वार्षिक ब्याज दर है, जो वार्षिक रूप से संचित होता है। ऋण को दो समान किस्तों में चुकाया गया, पहली एक वर्ष बाद और दूसरी एक वर्ष बाद। पहली किस्त ब्याज का एक वर्ष और मूलधन का एक भाग थी, जबकि दूसरी शेष मूलधन और उस पर देय ब्याज था। फिर प्रत्येक किस्त कितनी रुपये है? _________?
हल: हमें किश्तों और देय राशि की तुलना या तो उधार लेने के समय या पूरे ऋण के चुकाए जाने के समय करनी होगी।
आइए सभी मानों को उस समय सीमा में लाएं जिसमें सभी बकाया चुका दिए जाएं, यानी 2 साल के अंत तक।
जॉन ने बैंक से 10% प्रति वर्ष की दर से 2,10,000 रुपये उधार लिए।
2 साल के अंत तक यह ऋण 2,10,000*1.1*1.1 = 2,54,100 रुपये हो जाएगा।
माना कि हर साल किस्त के रूप में भुगतान की जाने वाली राशि x रुपये है।
जॉन पहली किस्त का भुगतान बाकी साल के अंत तक करेगा।
इसलिए, हमें पहले वर्ष के अंत से दूसरे वर्ष के अंत तक इस राशि पर ब्याज की गणना करनी होगी।
दूसरी किस्त का भुगतान होते ही ऋण चुक जाएगा। =
> 1.1x + x = 2,54,100
1,21,000.
इसलिए, 121000 सही उत्तर है.
उदाहरण 4: गोपाल ने अंकित से 8% वार्षिक ब्याज पर X रुपये उधार लिए। फिर उसने अपनी ओर से Y रुपये जोड़कर Ishan को 10% वार्षिक ब्याज पर X + Y रुपये उधार दिए। वर्ष के अंत में, अंकित के बकाया चुकाने के बाद, गोपाल के पास जो शुद्ध ब्याज बचता है, वह अंकित को मिले ब्याज के समान है। दूसरी ओर, यदि गोपाल ने Ishan को 10% पर X + 2Y रुपये उधार दिए होते, तो उसे जो शुद्ध ब्याज मिलता, वह 150 रुपये बढ़ जाता। यदि सभी ब्याज वार्षिक रूप से संचित होते हैं, तो X + Y का मान ज्ञात करें।
हल: यदि उधार ली गई राशि रु. (X+Y) है तो इशान द्वारा गोपाल को दिया गया ब्याज = 100 ∗ 10 (X+Y) = 0.1(X+Y)
गोपाल ने अंकित से भी 8% प्रति वर्ष की दर से रु. X उधार लिए।
इसलिए, उसे अंकित को उधार ली गई राशि पर ब्याज राशि के रूप में 0.08X रुपये वापस करना होगा।
इसलिए, गोपाल द्वारा रखा गया ब्याज = 0.1(X+Y) - 0.08X = 0.02X + 0.1Y ... (1)
यह दिया गया है कि गोपाल द्वारा रखा गया शुद्ध ब्याज अंकित को प्राप्त ब्याज के समान है।
इसलिए, 0.08X = 0.02X + 0.1Y ⇒ X = (5/3)Y 0 ... (2)
यदि उधार ली गई राशि रु. (X+2Y)
= 100 ∗ 10 (X+2Y) 0.1X+0.2Y
इस स्थिति में गोपाल द्वारा रखा गया ब्याज = 0.1X+0.2Y - 0.08X = 0.02X + 0.2Y ... (3)
यह दिया गया है कि गोपाल द्वारा रखा गया ब्याज दूसरे मामले में 150 रुपये बढ़ गया।
⇒ (0.02X + 0.2Y) - (0.02X + 0.1Y) = 150 Y
= 1500 रुपये
समीकरण (2) में Y का मान प्रतिस्थापित करके, हम कह सकते हैं कि
X = 2500 रुपये इसलिए, (X+Y) = 4000 रुपये
मूल्य का मूल्यह्रास
किसी मशीन या अन्य वस्तु का मूल्य जो कि घिसने और टूटने के अधीन है, समय के साथ घटता है। इस कमी को मूल्यह्रास कहा जाता है।
यदि A0 किसी निश्चित समय पर मूल्य है और r% प्रति वर्ष मूल्यह्रास की दर है, तो t वर्षों के अंत में मूल्य A1 होगा:
A 1 = A 0 (1 - r/100) t.
उदाहरण 1: लैपटॉप का मूल्य प्रति वर्ष 30% की दर से मूल्यह्रास होता है। यदि लैपटॉप का वर्तमान मूल्य रु. 40000 है। तो लैपटॉप का मूल्य दो वर्षों बाद क्या होगा?
a. रु. 28000
b. रु. 16000
c. रु. 24400
d. रु. 19600
हल: विकल्प 'घ' सही है।
व्याख्या: यहाँ प्रारंभिक मूल्य रु. 40000 दिया गया है, ब्याज की दर 30% प्रति वर्ष है, और समय अवधि 2 वर्ष है। तो, अंतिम मूल्य, A1 = 40000 x (1 – 70/100)² ⇒ 40000 x (0.30)² ⇒ 19600.
उदाहरण 2: 100000 रुपए की लागत से निर्मित एक आवासीय फ्लैट का मूल्य 10% प्रति वर्ष की दर से कम हो रहा है। निर्माण के 3 वर्ष बाद इसका मूल्य क्या होगा?
हल: जनसंख्या की वार्षिक वृद्धि दर = 5%
हमारे पास है: V 0 (प्रारंभिक मूल्य) = 100000 रुपये,
R= मूल्यह्रास की दर = 10% प्रति वर्ष,
n = 3 वर्ष।
इसलिए: 3 वर्ष बाद का मूल्य होगा,
V = 100000 x (1 - 10/100) 3
V = 100000 x (9/10 x 9/10 x 9/10)
V = 72900 रुपये
जनसंख्या आधारित प्रश्न
यह देखा गया है कि किसी विशेष क्षेत्र/राष्ट्र/आदि की जनसंख्या अपने पिछले मूल्य के सापेक्ष लगातार बढ़ती या घटती है,
अर्थात् यह पैसे के लिए चक्रवृद्धि ब्याज की तरह बढ़ती या घटती है।
इसलिए, हम जनसंख्या की गणना के लिए तुलनीय सूत्रों का उपयोग करते हैं।
- P1 = वृद्धि/गिरावट के बाद की अंतिम जनसंख्या
- P0 = प्रारंभिक जनसंख्या या वर्तमान जनसंख्या
- r% = जिस दर पर वृद्धि या गिरावट हो रही है
जब जनसंख्या बढ़ती है,
P1= P0(1 + r/100)n
जब जनसंख्या घटती है,
P1= P0(1 - r/100)n
उदाहरण 1: एक नगर की जनसंख्या 125000 है। यह वार्षिक 2% की दर से बढ़ रही है। 3 वर्षों के बाद इसकी जनसंख्या क्या होगी?
हल: वर्तमान जनसंख्या (P0) = 125000
वृद्धि की दर (R) = 2%
अवधि (n) = 3 वर्ष
∴ 3 वर्षों के बाद जनसंख्या = P1
P1 = 125000(1 + 2/100)3
= 125000(102/100 × 102/100 × 102/100)
P1 = 132651
उदाहरण 2: जनसंख्या की वार्षिक वृद्धि की दर 5% है। यदि किसी शहर की वर्तमान जनसंख्या 140000 है, तो तीन वर्षों के बाद उस शहर की जनसंख्या लगभग कितनी होगी?
a. 153000
b. 164000
c. 162000
d. 134000
हल: विकल्प 'c' सही है
व्याख्या: जनसंख्या की वार्षिक वृद्धि दर = 5%
एक शहर की वर्तमान जनसंख्या = 140000
प्रयुक्त सूत्र: शहर की जनसंख्या = P(1+r/100)
प्रश्न के अनुसार तीन वर्ष बाद शहर की जनसंख्या = P(1+r/100)
=140000(1+5/100) 3
= 140000(105/100) 3
= (140000 × 21/20 × 21/20 × 21/20)
= (1296540/8)
= 162067.5 ∼ 162000
तीन वर्ष बाद आवश्यक जनसंख्या 162000 है
उदाहरण 3: शहर की जनसंख्या 8% की दर से बढ़ रही है। यदि शहर की वर्तमान जनसंख्या 100000 है, तो 2 वर्षों के बाद जनसंख्या क्या होगी?
a. 115540
b. 126440
c. 116640
d. 126640
हल: विकल्प 'c' सही है
व्याख्या: मूलधन, P = 10000
दर, R = 8%
समय, n = 2 वर्ष
A = 100000 * (1 + 8/100)2
A= 100000 × (108/100) × (108/100)
A = 116640
2 वर्षों बाद जनसंख्या 116640 होगी।
|
142 videos|172 docs|185 tests
|
FAQs on बुनियादी अवधारणाएँ: साधारण ब्याज और चक्रवृद्धि ब्याज - Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA
| 1. साधारण ब्याज और चक्रवृद्धि ब्याज में क्या अंतर है? |  |
| 2. साधारण ब्याज की गणना कैसे की जाती है? |  |
| 3. चक्रवृद्धि ब्याज की गणना कैसे की जाती है? |  |
| 4. क्या चक्रवृद्धि ब्याज हमेशा साधारण ब्याज से अधिक होता है? |  |
| 5. साधारण और चक्रवृद्धि ब्याज का उपयोग कहाँ होता है? |  |