रुचियाँ: हल किए गए उदाहरण | Quantitative Aptitude/संख्यात्मक योग्यता - Bank Exams PDF Download
चलिए, सरल ब्याज और चक्रवृद्धि ब्याज पर हल किए गए प्रश्नों और उत्तरों में जाने से पहले बुनियादी सूत्रों पर नजर डालते हैं।
सभी ब्याज के सूत्र निम्नलिखित चर का उपयोग करते हैं: P = प्रारंभिक राशि; r = वार्षिक ब्याज दर; t = वर्षों की संख्या।
1) सरल ब्याज

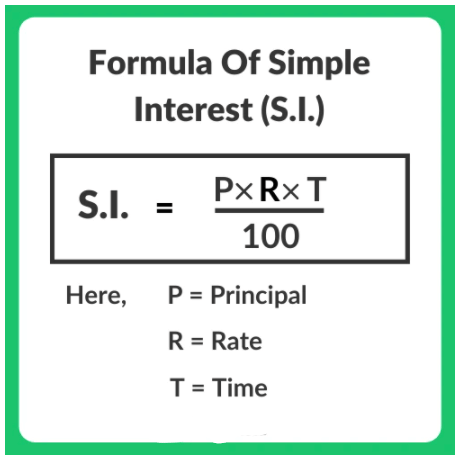
2) चक्रवृद्धि ब्याज

हल किए गए प्रश्न
प्रश्न 1: एक पिता ने अपनी दो बेटियों के बीच 35 लाख रुपये का वसीयतनामा छोड़ा, जिनकी उम्र 8.5 और 16 वर्ष है, ताकि जब वे 21 वर्ष की हों, तो उन्हें समान राशि मिले। 35 लाख रुपये की राशि को 10% वार्षिक सरल ब्याज पर निवेश करने के लिए कहा गया है। वसीयतनामे के समय बड़ी बेटी को कितनी राशि मिली? (1) 17.5 लाख (2) 21 लाख (3) 15 लाख (4) 20 लाख उत्तर: विकल्प 2
व्याख्या: मान लीजिए कि वसीयतनामे के समय बड़ी बेटी को मिली राशि Rs.x है। इसलिए, छोटी बेटी को मिली राशि (3,500,000 - x) होगी। बड़ी बेटी की राशि पर ब्याज (21 - 16) = 5 वर्षों के लिए 10% वार्षिक सरल ब्याज पर मिलता है।
छोटी बेटी की राशि पर ब्याज (21 - 8.5) = 12.5 वर्षों के लिए 10% वार्षिक सरल ब्याज पर मिलता है। चूंकि जब दोनों बेटियाँ 21 वर्ष की होंगी तब उन्हें मिली राशि समान होगी, => x = 2,100,000 = 21 लाख।
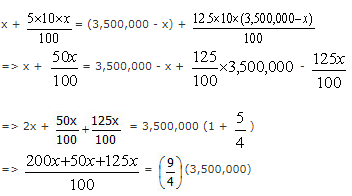
प्रश्न 2: यदि 1500 रुपये को 20% वार्षिक चक्रवृद्धि ब्याज पर तीन वर्षों के लिए निवेश किया जाए, तो यह कितने रुपये बनेगा? (1) 2400 (2) 2592 (3) 2678 (4) 2540 उत्तर: विकल्प 2
व्याख्या: चक्रवृद्धि ब्याज का सामान्य तरीका इस प्रकार है: A = .
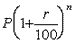
इस सूत्र में, A उस अवधि के अंत में राशि है जिसमें निवेश किया गया है, P वह राशि है जो निवेशित है, r ब्याज की दर है % p.a और n वह वर्षों की संख्या है जिसके लिए मूलधन निवेशित है। इस मामले में, यह A = होगा।
चक्रवृद्धि ब्याज में, ब्याज पर ब्याज दिया जाता है। पहले वर्ष में, ब्याज केवल मूलधन पर दिया जाता है। यह सरल ब्याज के समान है। हालांकि, दूसरे वर्ष से चीजें बदल जाती हैं। दूसरे वर्ष में, आप मूलधन पर और ब्याज पर ब्याज देते हैं। इसलिए, चक्रवृद्धि ब्याज में दूसरे वर्ष के अंत में राशि इस प्रकार की जा सकती है: 1 * मूलधन + 2 * मूलधन पर सरल ब्याज + 1 * ब्याज पर ब्याज।
इसी तरह, यदि आप चक्रवृद्धि ब्याज में तीन वर्षों के अंत में राशि ज्ञात करना चाहते हैं, तो निम्नलिखित विधि का उपयोग करें: 1 * मूलधन + 3 * मूलधन पर सरल ब्याज + 3 * ब्याज पर ब्याज + 1 * ब्याज पर ब्याज पर ब्याज।
आइए देखें कि यह हमारे उदाहरण में कैसे काम करता है। मूलधन 1500 रुपये है। ब्याज की दर 20% है। इसलिए, मूलधन पर सरल ब्याज 20% का 1500 = 300 रुपये है। ब्याज पर ब्याज = 20% ब्याज का 300 रुपये पर = 60 रुपये। ब्याज पर ब्याज पर ब्याज = 20% का 60 रुपये पर = 12 रुपये। अब, सभी को जोड़ें। तीन वर्षों के अंत में राशि = 1 * मूलधन + 3 * मूलधन पर सरल ब्याज + 3 * ब्याज पर ब्याज + 1 * ब्याज पर ब्याज पर ब्याज = 1500 + 3 * 300 + 3 * 60 + 1 * 12 = 1500 + 900 + 180 + 12 = 2592। यदि आपने सूत्र का उपयोग किया होता, तो आपको वही उत्तर मिलता। हालांकि, इस मामले में गणना करना सूत्र के उपयोग की तुलना में कहीं अधिक आसान था। चार और पांच वर्षों के लिए समान विधि का प्रयास करें और 1-2-1, 1-3-3-1, 1-4-6-4-1 आदि विधि को याद रखें, जिसका आप परीक्षा में आराम से उपयोग कर सकते हैं।
प्रश्न 3: यदि एक राशि दो वर्षों के लिए एक ऐसी योजना में निवेशित की जाती है जहाँ ब्याज वार्षिक रूप से संयुक्त होता है और वह राशि 144/121 गुना बढ़ जाती है, तो यदि उसी ब्याज दर पर सरल ब्याज विधि का उपयोग करते हुए निवेशित किया जाए, तो उसी राशि को तीन गुना होने में कितना समय लगेगा? (1) 9 वर्ष (2) 22 वर्ष (3) 18 वर्ष (4) 33 वर्ष उत्तर: विकल्प 2
व्याख्या: राशि 2 वर्षों में 144/121 गुना बढ़ जाती है। यदि P मूलधन है, तो यह दो वर्षों में P*(144/121) हो जाएगा जब इसे संयुक्त ब्याज में निवेशित किया जाता है। संयुक्त ब्याज में, यदि एक राशि को दो वर्षों के लिए निवेशित किया जाता है, तो राशि का पता निम्नलिखित सूत्र से लगाया जाता है: 144/121 P। यदि r = 100/11% है, तो सरल ब्याज में राशि को तीन गुना होने में लगने वाला समय इस प्रकार निकाला जाता है: मान लें कि P मूलधन है। इसलिए, यदि मूलधन तीन गुना हो जाता है = 3P, तो शेष 2P सरल ब्याज के कारण आया है। सरल ब्याज = Pnr/100, जहाँ P सरल ब्याज है, r ब्याज की दर है और ‘n’ वह संख्या है जिसमें मूलधन निवेशित था। इसलिए, 2P = 2 = n/11 या n = 22 वर्ष।
प्रश्न 4: तीन वर्ष पहले एक शहर की जनसंख्या 3600 थी। वर्तमान में यह 4800 है। यदि जनसंख्या की वृद्धि की दर वर्षों में स्थिर रही है और यह वार्षिक रूप से संयुक्त होती रही है, तो तीन वर्ष बाद जनसंख्या क्या होगी? (1) 6000 (2) 6400 (3) 7200 (4) 9600 उत्तर: विकल्प 2
व्याख्या: जनसंख्या 3 वर्षों में 3600 से 4800 हो गई। यह 3600 पर 1200 की वृद्धि है। इसलिए, तीन वर्षों में वृद्धि की दर 1200/3600 = 1/3 रही है। अगले तीन वर्षों में वृद्धि की दर भी समान होगी। इसलिए, जनसंख्या 4800 से 4800*1/3 = 1600 द्वारा बढ़ेगी। इसलिए, तीन वर्ष बाद जनसंख्या 4800 + 1600 = 6400 होगी।
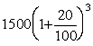

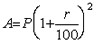
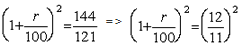
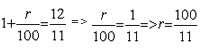
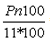
प्रश्न 5: एक व्यक्ति 5000 रुपये 3 वर्षों के लिए 5% वार्षिक चक्रवृद्धि ब्याज पर निवेश करता है। अर्जित ब्याज पर 20% आयकर प्रत्येक वर्ष के अंत में काटा जाता है। तीसरे वर्ष के अंत में राशि ज्ञात करें। (1) 5624.32 (2) 5630.50 (3) 5788.125 (4) 5627.20 उत्तर: विकल्प 1
व्याख्या: 5% ब्याज की दर है। ब्याज राशि का 20% कर के रूप में भुगतान किया जाता है। इसलिए ब्याज राशि का 80% बचता है। इसलिए, यदि हम ब्याज की दर को 5% का 80% मानते हैं = 4% प्रति वर्ष, तो हमें वही मान मिलेगा। चक्रवृद्धि ब्याज के लिए 3 वर्षों में अर्जित ब्याज = 3 * मूलधन पर साधारण ब्याज + 3 * साधारण ब्याज पर ब्याज + 1 * ब्याज पर ब्याज = 3 * (200) + 3 * (8) + 1 * 0.32 = 600 + 24 + 0.32 = 624.32। तीन वर्षों के अंत में राशि = 5000 + 624.32 = 5624.32।
प्रश्न 6: एक निश्चित राशि पर 12% प्रति वर्ष के लिए दो वर्षों में चक्रवृद्धि ब्याज और साधारण ब्याज के बीच का अंतर 90 रुपये है। तीन वर्षों के अंत में राशि का मूल्य क्या होगा? (1) 9000 (2) 6250 (3) 8530.80 (4) 8780.80 उत्तर: विकल्प 4
व्याख्या: दो वर्षों में साधारण ब्याज और चक्रवृद्धि ब्याज के बीच का अंतर पहले वर्ष के ब्याज पर ब्याज के कारण होता है जब ब्याज चक्रवृद्धि ब्याज के रूप में गणना किया जाता है, तो ब्याज वार्षिक रूप से चक्रित होता है। इसलिए, 12% साधारण ब्याज = 90 => साधारण ब्याज = 90/0.12 = 750। चूंकि एक वर्ष के लिए साधारण ब्याज = 750 @ 12% प्रति वर्ष है, तो मूलधन = 750/0.12 = 6250 रुपये। यदि मूलधन 6250 है, तो तीन वर्षों के अंत में शेष राशि = 6250 + 3(6250 का साधारण ब्याज) + 3(साधारण ब्याज पर ब्याज) + 1(ब्याज पर ब्याज) = 6250 + 3(750) + 3(90) + 1(10.80) = 8780.80।
प्रश्न 7: विजय ने ₹50,000 का निवेश किया, जिसका कुछ हिस्सा 10% पर और कुछ हिस्सा 15% पर लगाया। एक वर्ष के बाद उसकी कुल आय ₹7000 थी। उसने 10% की दर पर कितना निवेश किया? (1) ₹40,000 (2) ₹10,000 (3) ₹12,000 (4) ₹20,000 उत्तर: विकल्प 2
व्याख्या: इस समस्या को हल करने का सबसे अच्छा तरीका मिश्रण और अलिगेशन के सिद्धांत का उपयोग करना है। विजय ने ₹50,000 के निवेश पर ₹7000 की कुल आय अर्जित की। इसलिए, उसकी औसत वापसी की दर = 7000/50000 * 100। अलिगेशन के नियम के अनुसार, यदि किसी उत्पाद का मूल्य 10 (सस्ता) है और दूसरे का 15 (महंगा) है, और यदि दोनों को इस प्रकार मिलाया गया है कि मिश्रण का औसत मूल्य 14 (औसत मूल्य) है, तो दोनों उत्पादों का अनुपात इस प्रकार होगा। सस्ते उत्पाद का अनुपात: महंगे उत्पाद का अनुपात (महंगे उत्पाद का मूल्य - औसत मूल्य) : (औसत मूल्य - सस्ते उत्पाद का मूल्य)। हमारे उदाहरण में, सस्ता उत्पाद 10% पर किया गया निवेश है, महंगा उत्पाद 15% पर किया गया निवेश है और औसत मूल्य 14% की औसत वापसी है। इसलिए, 10% ब्याज पर निवेश की गई राशि = 1/5 * 50,000 = ₹10,000।
प्रश्न 8: एक निश्चित राशि जो 8% प्रति वर्ष साधारण ब्याज पर कुछ वर्षों के लिए निवेश की जाती है, वह ₹180 में बढ़ जाती है। वही राशि यदि 4% प्रति वर्ष साधारण ब्याज पर उसी संख्या के वर्षों के लिए निवेश की जाती है, तो वह केवल ₹120 में बढ़ जाती है। राशि कितने वर्षों के लिए निवेश की गई थी? (1) 25 वर्ष (2) 40 वर्ष (3) 33 वर्ष और 4 महीने (4) निर्धारित नहीं किया जा सकता उत्तर: विकल्प 1
व्याख्या: उपलब्ध जानकारी से हमें पता है कि, प्रधान 8% प्रति वर्ष ब्याज पर n वर्षों के लिए = 180 …….. (1) प्रधान 4% प्रति वर्ष ब्याज पर n वर्षों के लिए = 120 ……… (2) समीकरण (2) को समीकरण (1) से घटाने पर, हमें मिलता है 4% प्रति वर्ष ब्याज पर n वर्षों के लिए = ₹60। अब, हम इस मान को समीकरण (2) में प्रतिस्थापित कर सकते हैं, यानी प्रधान 60 = 120 = प्रधान = ₹60। हमें पता है कि साधारण ब्याज = pnr/100, जहाँ p प्रधान है, n वर्षों की संख्या है और r ब्याज की दर है। समीकरण (2) में, p = ₹60, r = 4% प्रति वर्ष और साधारण ब्याज = ₹60। इसलिए, 60 = (60*n*4)/100 => n = 100/4 = 25 वर्ष।
प्रश्न 9: यदि एक राशि को 12.5% प्रति वर्ष साधारण ब्याज पर निवेशित किया जाता है, तो यह राशि Rs.1250 से बढ़कर Rs.10,000 होने में कितना समय लेगी? (1) 8 वर्ष (2) 64 वर्ष (3) 72 वर्ष (4) 56 वर्ष उत्तर: विकल्प 4 व्याख्या:
- साधारण ब्याज का सूत्र है SI = (pnr/100), जहाँ p = मूलधन, n = वर्षों की संख्या, r = वार्षिक ब्याज दर।
- इस मामले में, Rs. 1250 का मूल्य Rs.10,000 हो गया है। इसलिए, अर्जित ब्याज = 10,000 – 1250 = 8750।
- 8750 = [(1250 x n x 12.5)/100] => n = 700 / 12.5 = 56 वर्ष।
प्रश्न 10: Rs. 5887 को श्याम और राम के बीच इस प्रकार विभाजित किया गया है कि 9 वर्षों के अंत में श्याम का हिस्सा राम के 11 वर्षों के अंत में हिस्से के बराबर है, जिसे 5% की वार्षिक दर पर चक्रवृद्धि ब्याज पर लगाया गया। श्याम का हिस्सा ज्ञात करें। (1) 2088 (2) 2000 (3) 3087 (4) इनमें से कोई नहीं उत्तर: विकल्प 3 व्याख्या:
- श्याम का हिस्सा * (1 + 0.05)9 = राम का हिस्सा * (1 + 0.05)11
- श्याम का हिस्सा / राम का हिस्सा = (1 + 0.05)11 / (1 + 0.05)9 = (1 + 0.05)2 = 441/400
- इसलिए श्याम का हिस्सा = (441/841) * 5887 = 3087।
प्रश्न 11: आज का प्रश्न साधारण और चक्रवृद्धि ब्याज के विषय से है। शॉन ने अपनी बचत का आधा हिस्सा एक बांड में निवेश किया, जिसने 2 वर्षों के लिए साधारण ब्याज दिया और उसे ब्याज के रूप में Rs.550 प्राप्त हुए। उसने शेष राशि को एक बांड में निवेश किया जिसने चक्रवृद्धि ब्याज दिया, ब्याज वार्षिक रूप से चक्रित होता है, उसी 2 वर्षों के लिए एक ही ब्याज दर पर और उसे ब्याज के रूप में Rs.605 प्राप्त हुए। इन दोनों बांडों में निवेश करने से पहले उसकी कुल बचत का मूल्य क्या था? (1) Rs.5500 (2) Rs.11000 (3) Rs.22000 (4) Rs.2750 उत्तर: विकल्प 4
व्याख्या: शैन ने अपने संयोजित ब्याज वाले बांड पर अतिरिक्त राशि (Rs.605 - Rs.550) Rs.55 प्राप्त की, क्योंकि पहले वर्ष में प्राप्त ब्याज ने दूसरे वर्ष में भी ब्याज अर्जित किया। संयोजित ब्याज बांड पर अर्जित अतिरिक्त ब्याज = Rs.55 पहले वर्ष का ब्याज = 550/2 = Rs.275 इसलिए, ब्याज की दर = 55/275 * 100 = 20% प्रति वर्ष। 20% ब्याज का अर्थ है कि शैन ने बांड में निवेश की गई राशि का 20% ब्याज के रूप में प्राप्त किया। यदि उसके एक बांड में निवेश का 20% = Rs.275 है, तो उसके प्रत्येक बांड में कुल निवेश = 275/20 * 100 = 1375 है। चूंकि उसने दोनों बांड में समान राशि का निवेश किया, इसलिए उसके कुल बचत का योग = 2*1375 = Rs.2750।
प्रश्न 12: Rs.100 5 वर्षों में वार्षिक संयोजित ब्याज पर दोगुना हो जाता है। एक और Rs.200 संयोजित ब्याज प्राप्त करने में और कितने वर्ष लगेंगे? (1) 10 वर्ष (2) 5 वर्ष (3) 7.5 वर्ष (4) 15 वर्ष (5) 8 वर्ष उत्तर: विकल्प 2
व्याख्या: Rs.100 का संयोजित ब्याज 5 वर्षों में Rs.200 हो जाता है। राशि फिर से 5 वर्षों में दोगुनी होगी। अर्थात्, राशि अगले 5 वर्षों में Rs.400 हो जाएगी। इसलिए, एक और Rs.200 ब्याज कमाने के लिए, इसे और 5 वर्ष लगेंगे।
प्रश्न 13: वर्ष 2004 की शुरुआत में, एक व्यक्ति ने एक बैंक में कुछ राशि का निवेश किया। वर्ष 2007 की शुरुआत में, संचित ब्याज Rs.10,000 है और वर्ष 2010 की शुरुआत में, संचित ब्याज Rs.25,000 हो जाता है। ब्याज की दर वार्षिक संयोजित है और वार्षिक ब्याज दर निश्चित है। प्रधान राशि _____ है: (1) Rs.16,000 (2) Rs.18,000 (3) Rs.20,000 (4) Rs.25,000 (5) उपरोक्त में से कोई नहीं उत्तर: विकल्प 3 व्याख्या:
2004 की शुरुआत से 2007 की शुरुआत तक (3 वर्षों के लिए) ब्याज = ₹10,000
2004 की शुरुआत से 2010 की शुरुआत तक (6 वर्षों के लिए) ब्याज = ₹25,000
परिवर्तनीय निर्धारित: मान लें कि प्रधान राशि = x और वार्षिक ब्याज दर = 100r%
जब एक राशि को संवृद्धि ब्याज में निवेश किया जाता है, तो राशि की गणना करने का सूत्र निम्नलिखित है:
जहाँ A राशि है, P प्रधान राशि है, r वार्षिक ब्याज दर % में है और n वर्षों की संख्या है। हमने x को प्रधान राशि और 100r% को ब्याज दर के रूप में निर्धारित किया है।
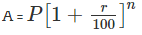
∴ 3 वर्षों के लिए राशि A3 = x(1 + r)3 = x 10000 (राशि = प्रधान + ब्याज)
और 6 वर्षों के लिए राशि A6 = x(1 + r)6 = x 25000
अधिकांश मान लें, (1 + r)3 = a
तब, x(1 + r)3 = xa = x 10000 ..... (1)
और x(1 + r)6 = xa2 = x 25000 ..... (2)
दोनों समीकरणों को हल करें ताकि x मिल सके:
- x(a – 1) = 10000 ..... (1)
- x(a2 – 1) = 25000 ..... (2)
दोनों समीकरणों में x के पदों को एक तरफ लाते हुए, हम दो समीकरणों को इस प्रकार पुनः लिख सकते हैं:
- x(a – 1) = 10000
- x(a2 – 1) = 25000
इसलिए समीकरण (2) को इस प्रकार व्यक्त किया जा सकता है:
x(a2 – 1) = x(a - 1)(a + 1) = 25000
हम जानते हैं कि समीकरण (1) से x(a – 1) = 10000
समीकरण (2) में x(a – 1) = 10000 को प्रतिस्थापित करें।
∴ x(a - 1)(a + 1) = 10000(a + 1) = 25000
या, (a + 1) = 25000/10000 = 2.5
यदि a + 1 = 2.5, तो a – 1 = (a + 1 – 2) = 2.5 – 2 = 0.5
समीकरण (1) से हमें ज्ञात है कि x(a – 1) = 10000
हमने गणना की है (a – 1) = 0.5
इसलिए, x = 10000/0.5 = 20000।
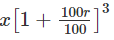
|
30 videos|172 docs|185 tests
|




















