महत्वपूर्ण सूत्र और सुझाव: समय और कार्य | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download

प्रश्नों और महत्वपूर्ण सूत्रों पर आगे बढ़ने से पहले, उम्मीदवारों के लिए यह आवश्यक है कि वे इस संकल्पना और परीक्षा में पूछे जा सकने वाले प्रश्नों के प्रकार को अच्छे से समझ लें।

समय और कार्य की संकल्पना इस बात के इर्द-गिर्द घूमती है कि किसी व्यक्ति या लोगों के समूह को एक कार्य पूरा करने में कितना समय लगता है, साथ ही उनके कार्य की प्रभावशीलता भी। यह समझने में मदद करती है कि प्रत्येक व्यक्ति कार्य के समग्र पूर्णता में कितनी कुशलता से योगदान देता है।

नीचे समय और कार्य विषय के संदर्भ में परीक्षा में पूछे जा सकने वाले मूल प्रश्नों के प्रकार दिए गए हैं:

• व्यक्ति की कुशलता की गणना करना।
• व्यक्ति द्वारा एक विशिष्ट कार्य पूरा करने के लिए आवश्यक समय निर्धारित करना।
• किसी समूह द्वारा एक विशेष कार्य को खत्म करने के लिए आवश्यक समय का अनुमान लगाना।
• दी गई समय अवधि में एक व्यक्ति द्वारा किए गए कार्य की मात्रा का मूल्यांकन करना।
• निर्धारित समय सीमा के भीतर एक समूह द्वारा किए गए संयुक्त कार्य का मूल्यांकन करना।

उपयोग किए गए सूत्र

सूत्रों का ज्ञान प्रश्न का सामना करते ही आपको समाधान से तुरंत जोड़ सकता है। इसलिए, किसी भी संख्यात्मक क्षमता विषय के लिए सूत्रों से अवगत होना समाधान प्रक्रिया और संबंधित गणनाओं को सरल बनाता है।

प्रश्नों को हल करने से पहले, यह महत्वपूर्ण है कि आप इस विषय की मूल संकल्पना, मानक सूत्रों, और उसी के लिए प्रश्नों के प्रकार से भलीभांति परिचित हों।

• कार्य किया गया = समय लिया × कार्य की दर
• कार्य की दर = 1 / समय लिया
• समय लिया = 1 / कार्य की दर
• यदि A एक कार्य को n दिनों में कर सकता है, तो A द्वारा 1 दिन में किया गया कार्य = 1/n। यदि A एक दिन में 1/n कार्य करता है, तो A कार्य को n दिनों में पूरा कर सकता है।
• कुल कार्य किया गया = दिनों की संख्या × कुशलता
• कुशलता और समय एक-दूसरे के विपरीत अनुपात में होते हैं।
• A एक विशेष कार्य को ‘a’ घंटों में करता है और B उसी कार्य को ‘b’ घंटों में करता है, तो मिलकर उन्हें कार्य पूरा करने में:
• A एक विशेष कार्य को ‘a’ घंटों में करता है जबकि B उसी कार्य को ‘b’ घंटों में करता है, फिर मिलकर उन्हें कार्य पूरा करने में घंटों का समय लगेगा।
• x:y उन पुरुषों की संख्या का अनुपात है जो एक कार्य को पूरा करने के लिए आवश्यक हैं, तो कार्य को पूरा करने में उनके द्वारा लिए गए समय का अनुपात y:x होगा।
• यदि M1 पुरुष W1 कार्य को D1 दिनों में T1 कार्य घंटों/दिन में कर सकते हैं और M2 पुरुष W2 कार्य को D2 दिनों में T2 कार्य घंटों/दिन में कर सकते हैं, तो:

समय और कार्य सूत्र- मजदूरी के आधार पर

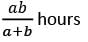
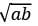
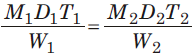
1) कुल वेतन = कुल दिनों की संख्या × किसी व्यक्ति के दैनिक वेतन का वेतन

2) वेतन काम की मात्रा के साथ सीधे अनुपात में होता है और

3) वेतन उस संख्या के साथ सीधे अनुपात में होता है जितने घंटे प्रत्येक व्यक्ति एक दिन में काम करता है।

4) वेतन उस समय के साथ विलोम अनुपात में होता है जो कर्मचारी द्वारा खर्च किया गया है।

5) यदि A और B क्रमशः x और y दिनों में कोई कार्य पूरा कर सकते हैं, तो उनका वेतन y:x अनुपात में दिया जाएगा। इसलिए, A और B का वेतन होगा

कुल वेतन y/(x + y) = A का वेतन।

कुल वेतन x/(x + y) = B का वेतन।

कुछ याद रखने के टिप्स

• A एक विशेष कार्य ‘a’ घंटों में करता है, B वही कार्य ‘b’ घंटों में करता है और C वही कार्य ‘c’ घंटों में करता है, तो वे मिलकर (abc/ab + bc + ca) घंटे लेंगे।
• यदि A एक विशेष कार्य ‘a’ घंटों में करता है और A&B मिलकर वह कार्य ‘t’ घंटों में करते हैं, तो B अकेले उसे (at/a - t) घंटों में करेगा।
• यदि A एक विशेष कार्य ‘a’ घंटों में करता है, B वही कार्य ‘b’ घंटों में करता है और ABC मिलकर वह कार्य ‘t’ घंटों में करते हैं, तो ⇒ C अकेले इसे (abt/ab - at - bt) घंटों में कर सकता है। ⇒ A और C मिलकर इसे (bt/b - t) घंटों में कर सकते हैं। ⇒ B और C मिलकर इसे (at/a - t) घंटों में कर सकते हैं।
• यदि उद्देश्य टैंक भरना है, तो इनलेट पाइप सकारात्मक कार्य करते हैं जबकि आउटलेट पाइप नकारात्मक कार्य करते हैं। यदि उद्देश्य टैंक खाली करना है, तो आउटलेट पाइप सकारात्मक कार्य करते हैं जबकि इनलेट पाइप नकारात्मक कार्य करते हैं।

समय और कार्य की तरकीबें

बुनियादी सूत्रों के अलावा, चलिए समय और कार्य पर आधारित समस्याओं को अधिक तेजी से हल करने के लिए कुछ संक्षिप्त तरिके सीखते हैं।

• A यदि ‘n’ दिनों में कार्य कर सकता है, तो A की कार्यक्षमता “1/n” है।
• यदि व्यक्तियों ने W1 कार्य को D1 दिनों में T1 घंटे प्रति दिन काम करके पूरा किया और M व्यक्तियों ने W2 कार्य को D2 दिनों में T2 घंटे प्रति दिन काम करके पूरा किया, तो उनके बीच का संबंध है।
• यदि A और B प्रत्येक एक काम को days में पूरा कर सकते हैं, तो (A Bone ) का दिन का कार्य-

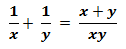
• (A और B) को कार्य पूरा करने के लिए समय –

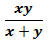
• यदि ‘n’ लोग (दो से अधिक) हैं, तो उनके द्वारा एक दिन में किया गया कार्य समान है जहाँ x1, x2, और x3 उस कार्य को पूरा करने में लगे दिनों को दर्शाते हैं।

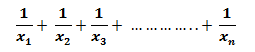
• यदि A को कार्य पूरा करने के लिए (A और B) से अधिक दिन लगते हैं और B को भी उसी कार्य को करने के लिए (A और B) से y दिन अधिक लगते हैं, तो (A और B) उस कार्य को √xy दिनों में पूरा करते हैं।
• यदि A और B एक कार्य को x दिनों में पूरा कर सकते हैं और A इसे अकेले y दिनों में कर सकता है, तो B को कार्य पूरा करने के लिए कितने दिन चाहिए-

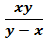
• यदि A और B एक कार्य को x दिनों में पूरा कर सकते हैं, B और C वही कार्य y दिनों में पूरा कर सकते हैं, और A और C इसे z दिनों में पूरा कर सकते हैं, तो A, B, और C मिलकर उस कार्य को पूरा करने में-

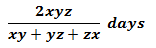
• यदि A एक कार्य को days में पूरा कर सकता है और B इसे A की तुलना में जल्दी कर सकता है, तो B उस कार्य को days में पूरा करेगा।

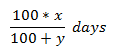
आइए समय और कार्य पर कुछ प्रश्नों को हल करें।

हल किए गए प्रश्न: समय और कार्य

प्रश्न 1: एक बिल्डर अपने एक निर्माण स्थल पर तीन श्रमिकों, आकाश, सुनील और राकेश को नियुक्त करता है। वे क्रमशः 20, 30 और 60 दिनों में एक कार्य पूरा करते हैं। यदि आकाश को हर तीसरे दिन सुनील और राकेश की सहायता मिलती है, तो आकाश को पूरा कार्य करने में कितने दिन लगेंगे?

• 10 दिन
• 15 दिन
• 25 दिन
• 30 दिन
• 45 दिन

समाधान:

उत्तर: (2) 15 दिन

आकाश, सुनील और राकेश द्वारा 1 दिन में किया गया कुल कार्य = {(1/20) + (1/30) + (1/60)} = 1/10

आकाश द्वारा 2 दिन में किया गया कार्य = (1/20) × 2 = 1/10

3 दिनों में किया गया कार्य (सभी तीनों का 1 दिन और आकाश का 2 दिन) = (1/10) + (1/10) = 1/5

इसलिए, 3 दिनों में किया गया कार्य = 1/5

कार्य पूरा करने में लगने वाला समय = 5×3 = 15 दिन

प्रश्न 2: एक कार्य को पूरा करने के लिए, समीर को 6 दिन और तानवीर को 8 दिन लगते हैं। समीर और तानवीर ने इस कार्य के लिए 2400 रुपये लिए। जब अमीर ने उन दोनों का साथ दिया, तो कार्य 3 दिनों में पूरा हुआ। अमीर को कितना भुगतान किया गया?

• Rs. 300
• Rs. 400
• Rs. 800
• Rs. 500
• Rs. 100

उत्तर: (1) Rs.300

समीर और तानवीर द्वारा किया गया कुल कार्य = {(1/6) + (1/8)} = 7/24

1 दिन में अमीर द्वारा किया गया कार्य = (1/3) – (7/24) = 1/24

उनमें से प्रत्येक के बीच वितरित राशि = (1/6) : (1/8) : (1/24) = 4:3:1

अमीर को भुगतान की गई राशि = (1/24) × 3 × 2400 = Rs.300

प्रश्न 3: देव ने विद्यालय परियोजना को 20 दिनों में पूरा किया। यदि अरुण देव से 25% अधिक सक्षम है, तो अरुण को वही कार्य पूरा करने में कितने दिन लगेंगे?

• 12 दिन
• 16 दिन

उत्तर: (3) 16 दिन

मान लें कि अरुण को कार्य पूरा करने में लगने वाले दिन x हैं।

अरुण और देव द्वारा लिए गए समय का अनुपात = 125:100 = 5:4

5:4 :: 20:x ⇒ x = {(4×20) / 5} ⇒ x = 16

प्रश्न 4: A को कोई कार्य पूरा करने में लगने वाला समय B द्वारा लगाए गए समय का दो गुना है और C द्वारा लगाए गए समय का तीन गुना है। यदि तीनों मिलकर काम करते हैं, तो उन्हें पूरा कार्य करने में 2 दिन लगते हैं। B अकेले इस कार्य को पूरा करने में कितना समय लगाएगा?

• निर्धारित नहीं किया जा सकता

उत्तर: (2) 6 दिन
A द्वारा लगने वाला समय = x दिन
B द्वारा लगने वाला समय = x/2 दिन
C द्वारा लगने वाला समय = x/3 दिन
⇒ {(1/x) + (2/x) + (3/x) = 1/2 ⇒ 6/x = 1/2 ⇒ x = 12
B द्वारा लगने वाला समय = x/2 = 12/2 = 6 दिन

प्रश्न 5: सोनल और प्रीति ने एक परियोजना पर काम करना शुरू किया और वे इस परियोजना को 30 दिनों में पूरा कर सकते हैं। सोनल ने 16 दिन काम किया और प्रीति ने शेष कार्य को 44 दिनों में पूरा किया। यदि प्रीति अकेले पूरी परियोजना को पूरा करती, तो उसे कितने दिन लगते?

• 55 दिन
• 46 दिन

उत्तर: (5) 60 दिन
मान लें कि सोनल द्वारा 1 दिन में किया गया कार्य x है
मान लें कि प्रीति द्वारा 1 दिन में किया गया कार्य y है
तब, x + y = 1/30 ——— (1)
⇒ 16x + 44y = 1 ——— (2)
समीकरण (1) और (2) को हल करते हैं, x = 1/60, y = 1/60
इस प्रकार, प्रीति पूरी कार्य को 60 दिनों में पूरा कर सकती है।

प्रश्न 6: पंप A को अकेले एक टैंक पानी भरने में 6 घंटे लगते हैं। पंप B को अकेले उसी टैंक को भरने में 8 घंटे लगते हैं। हम तीन पंपों: A, B और एक अन्य पंप C का उपयोग करना चाहते हैं ताकि टैंक को 2 घंटे में भरा जा सके। पंप C की दर क्या होनी चाहिए? पंप C को अकेले टैंक भरने में कितना समय लगेगा?

मान लें कि टैंक की कुल क्षमता C लीटर है।

पंप A की भरने की दर, Fa = C/6 लीटर प्रति घंटा

पंप B की भरने की दर, Fb = C/8 लीटर प्रति घंटा

2 घंटे x [Fa + Fb + Fc] = C => Fc = 5C/24 लीटर प्रति घंटा

मान लेते हैं कि टैंक भरने में केवल पंप C द्वारा लिया गया समय 't' है।

‘t’ घंटे x 5C/24 = C => t = 24/5 = 4.8 घंटे

प्रश्न 7: A अकेले एक कार्य 6 दिनों में कर सकता है और B अकेले 8 दिनों में। A और B ने इसे Rs.3200 में करने का निश्चय किया। C की सहायता से, उन्होंने कार्य 3 दिनों में पूरा किया। C को कितना भुगतान किया जाएगा?

मान लेते हैं कि कार्य का कुल मात्रा W इकाइयाँ हैं।

A की उत्पादकता, Pa = W/6 इकाइयाँ प्रति दिन।

B की उत्पादकता, Pb = W/8 इकाइयाँ प्रति दिन।

3 दिन x [Pa Pb Pc] = W => Pc = W/24 इकाइयाँ प्रति दिन

A, B और C के वेतन का अनुपात = उनकी उत्पादकताओं के अनुपात = (W/6): (W/8): (W/24) = 4: 3: 1।

C को भुगतान की जाने वाली राशि = Rs.3200 x (1/8) = Rs.400

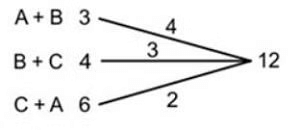
प्रश्न 8: A और B किसी कार्य को 3 दिनों में कर सकते हैं; B और C इसे 4 दिनों में कर सकते हैं और A और C इसे 6 दिनों में कर सकते हैं। A, B और C यदि साथ में काम करते हैं, तो इसे कितने दिनों में समाप्त करेंगे?

3, 4, और 6 का LCM = 12 (कुल कार्य) 2(A B C) की दक्षता = 9 (A B C) की दक्षता = 4.5 समय = 12 / (9/2) = 8/3 दिन

प्रश्न 9: P Q से दो गुना अच्छा है और वे मिलकर एक कार्य 36 दिनों में पूरा करते हैं। P अकेले कार्य पूरा करने में कितने दिन लेगा?

समाधान: दिया गया,

P Q से दो गुना अच्छा है।

⇒ (P का 1 दिन का कार्य) / (Q का 1 दिन का कार्य) = 2 / 1 दिया गया,

⇒ (P Q का 1 दिन का कार्य) = 1/36

⇒ P का 1 दिन का कार्य = (1/36) × (2/3) = 1/54

∴ P अकेले 54 दिनों में कार्य पूरा कर सकता है।

प्रश्न 10: A और B क्रमशः 15 दिनों और 10 दिनों में एक कार्य पूरा कर सकते हैं। उन्हें Rs. 75000 में कार्य पूरा करने का अनुबंध मिला। अनुबंधित राशि में B का हिस्सा (Rs. में) कितना होगा:

समाधान: A और B द्वारा कार्य पूरा करने में लिए गए दिनों का अनुपात = 15 : 10 = 3 : 2

∴ A और B की कार्यक्षमता का अनुपात = 2 : 3 मान लें कि उनका हिस्सा 2x और 3x के अनुपात में है। अब,

2x + 3x = 75000

⇒ 5x = 75000

∴ x = 15000

∴ B का हिस्सा = 3x = 15000 × 3 = 45000 रुपए