त्रिभुज | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download
क्या है एक त्रिकोण?
- एक त्रिकोण तीन भुजाओं वाला एक बहुभुज है।
- त्रिकोणों को दो सामान्य तरीकों से वर्गीकृत किया जाता है: उनकी भुजाओं के आधार पर और उनके कोणों के आधार पर।
त्रिकोण के प्रकार
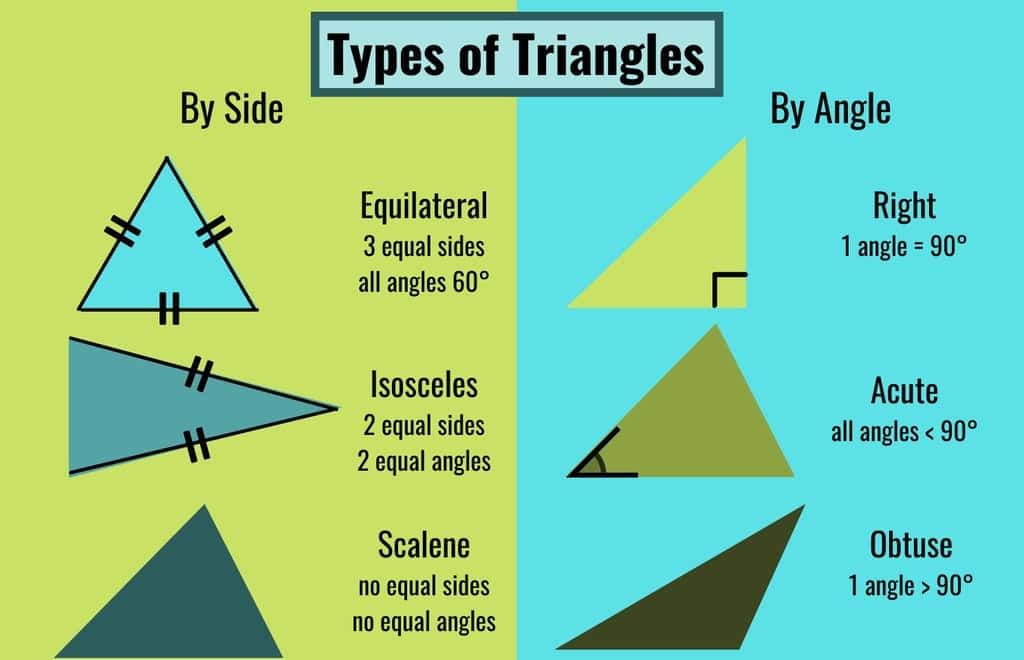
भुजाओं के आधार पर, त्रिकोणों को तीन श्रेणियों में वर्गीकृत किया गया है:
- स्केलन त्रिकोण: एक त्रिकोण जिसमें तीन भुजाएँ विभिन्न लंबाई की होती हैं, उसे स्केलन त्रिकोण कहा जाता है।
- आइसोसेल्स त्रिकोण: एक आइसोसेल्स त्रिकोण में दो समान भुजाएँ होती हैं। तीसरी भुजा को आधार कहा जाता है। समान भुजाओं के विपरीत कोण भी समान होते हैं।
- समान्तर त्रिकोण: एक समान्तर त्रिकोण में तीन समान भुजाएँ होती हैं। इस प्रकार के त्रिकोण में कोण भी समान होते हैं, इसलिए इसे समान कोणीय त्रिकोण भी कहा जा सकता है। एक समान्तर त्रिकोण का प्रत्येक कोण 60° होना चाहिए, क्योंकि किसी भी त्रिकोण के आन्तरिक कोणों का योग 180° होना चाहिए।

त्रिकोणों को आन्तरिक कोणों के माप के आधार पर भी तीन श्रेणियों में विभाजित किया जाता है:
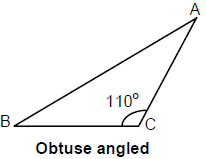
- अधिक कोणीय त्रिकोण: जब त्रिकोण का सबसे बड़ा कोण 90° से अधिक होता है, तो इसे अधिक कोणीय त्रिकोण कहा जाता है। चित्र में ΔABC एक अधिक कोणीय त्रिकोण है जहाँ C एक अधिक कोण है।
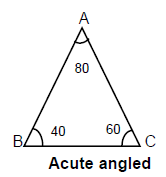
- तेज कोणीय त्रिकोण: जिसमें सभी कोण 90° से कम होते हैं, जैसे ΔPQR एक तेज त्रिकोण है क्योंकि इसका सबसे बड़ा कोण 90° से कम है।
- समकोण त्रिकोण: एक त्रिकोण जिसका एक कोण 90° होता है, उसे समकोण त्रिकोण कहा जाता है। चित्र में, b हाइपोटेन्यूज है, और a एवं c को आधार और ऊँचाई कहा जाता है। समकोण त्रिकोण ABC में, a² + b² = c²।
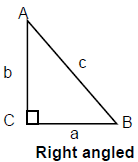

त्रिकोण के गुण
तीन कोणों का योग 180° है।
- किसी भी त्रिकोण के बाहरी कोणों का योग 360° के बराबर होता है।
- एक बाहरी कोण आंतरिक विपरीत कोणों के योग के बराबर होता है।
- दो भुजाओं का योग हमेशा तीसरी भुजा से बड़ा होता है।
- किसी भी दो भुजाओं के बीच का अंतर हमेशा तीसरी भुजा से कम होता है।
- जिस कोण का मान सबसे बड़ा होता है, उसके विपरीत की भुजा सबसे बड़ी होती है और जिस कोण का मान सबसे छोटा होता है, उसके विपरीत की भुजा सबसे छोटी होती है।
- यदि ΔABC एक समकोण त्रिकोण है, तो ∠B 90° के बराबर होगा जब तक कि अन्यथा न कहा जाए।
- एक समकोण त्रिकोण में जिसके कोण 30°, 60°, 90° हैं, इस त्रिकोण में 30° के विपरीत भुजा = कर्ण, और 60° के विपरीत भुजा = कर्ण।
- केंद्रीय बिंदु (Centroid): (a) यह त्रिकोण की माध्य रेखाओं का संविलयन बिंदु है। (माध्य रेखा वह रेखा है जो एक शीर्ष को विपरीत भुजा के मध्य बिंदु से जोड़ती है)। (b) केंद्रीय बिंदु प्रत्येक माध्य रेखा को शीर्ष से 2:1 के अनुपात में विभाजित करता है। (c) माध्य रेखा की लंबाई ज्ञात करने के लिए हम अपोलोनियस का सिद्धांत का उपयोग करते हैं। AB² + AC² = 2(AD² + BD²) (d) माध्य रेखाएँ त्रिकोण के क्षेत्रफल को आधा कर देंगी। (e) यदि x, y, z त्रिकोण ABC के माध्यमों की लंबाई हैं, तो "चार गुना माध्य रेखाओं के वर्गों का योग त्रिकोण की भुजाओं के वर्गों के योग के तीन गुना के बराबर है"। 4(x² + y² + z²) = 3(a² + b² + c²)।
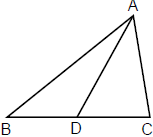
- ऊर्ध्वकोण (Orthocentre): यह ऊँचाईयों का संविलयन बिंदु है। (ऊँचाई वह लंब perpendicular है जो त्रिकोण के एक शीर्ष से विपरीत भुजा पर खींची जाती है)। समकोण त्रिकोण में, ऊर्ध्वकोण वह शीर्ष होता है, जहाँ समकोण होता है।
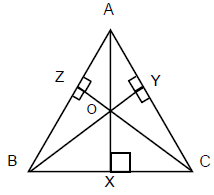
- परिकेंद्र (Circumcentre): यह त्रिकोण की भुजाओं के लंबवृत्तों का संविलयन बिंदु है। (a) त्रिकोण का परिकेंद्र उस वृत्त का केंद्र होता है जो त्रिकोण के शीर्षों के माध्यम से गुजरता है। (b) परिकेंद्र शीर्षों से समान दूरी पर होता है। (c) यदि a, b, c त्रिकोण की भुजाएँ हैं, Δ क्षेत्रफल है, तो abc = 4RΔ, जहाँ R परिकेन्द्र वृत्त का त्रिज्या है।
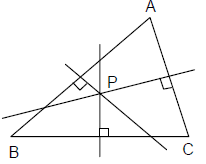
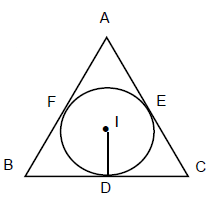
- इंसेंटरे (Incentre): यह त्रिकोण के कोणों के आंतरिक बाईसकटर्स का संविलयन बिंदु है। (c) Δ = rs यदि r इंसर्कल की त्रिज्या है, जहाँ s = अर्ध-परिमाप = और Δ त्रिकोण का क्षेत्रफल है। (d) BF = BD = s – b जहाँ 2s = a + b + c, CE = CD = s – c, AF = AD = s – a (e) आंतरिक बाईसकटर्स और बाहरी बाईसकटर्स के बीच का कोण 90° होता है।
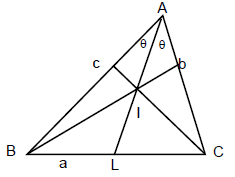
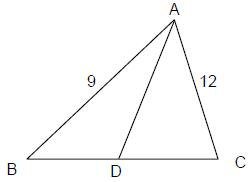
उदाहरण: 1 ΔABC में, AB = 9, BC = 10, AC = 12। A के माध्यम से माध्य रेखा की लंबाई ज्ञात करें।
पड़ोसी चित्र में AD आवश्यक मध्य है। त्रिकोण में अपोलोनियस का प्रमेय का उपयोग करते हुए, हमारे पास है, 2AD2 + 2(5)2 = 81 + 144। 2AD2 = 50 = 225
- अपोलोनियस का प्रमेय: 2AD2 + 2(5)2 = 81 + 144। 2AD2 = 50 = 225
उदाहरण 2: त्रिकोण की भुजाएँ 6 सेमी, 8 सेमी, और 10 सेमी हैं। त्रिकोण का क्षेत्रफल, अंतरक और परिक्रमण ज्ञात करें।
- s =
➢ समान्तर त्रिकोण
एक समान्तर त्रिकोण में, सभी भुजाएँ समान होती हैं और सभी कोण समान होते हैं। (क) उचाई =
(ख) क्षेत्रफल =
(ग) अंतरक =
(घ) परिक्रमण =
➢ समानता
- दो या दो से अधिक आकृतियों को तब ही समान कहा जा सकता है जब वे सभी एक समान आकार और आकृति की हों। यदि हम समतल आकृतियों के बारे में बात करते हैं, तो वे तब समान होती हैं जब उनके संबंधित भुजाएँ और कोण दूसरी आकृति की संबंधित भुजाओं और कोणों के बराबर हों। उदाहरण: यदि दो त्रिकोण ABC और DEF सभी पहलुओं में समान हैं (आकार और आकार में समान), तो उन्हें समान कहा जाता है। समानता का संकेत ≅ या ≡ है।
➢ समान त्रिकोण
- यदि ∠A = ∠D, ∠B = ∠E, ∠C = ∠F, AB = DE, BC = EF; AC = DF, तो ΔABC ≡ ΔDEF या ΔABC ≅ ΔDEF।
समानता के परीक्षण:
- (a) SAS परीक्षण: पहले त्रिकोण की दो भुजाएँ और समाविष्ट कोण दूसरे त्रिकोण की दो भुजाओं और समाविष्ट कोण के बराबर हैं।
- (b) SSS परीक्षण: एक त्रिकोण की तीन भुजाएँ दूसरी त्रिकोण की तीन भुजाओं के बराबर हैं।
- (c) ASA परीक्षण: एक त्रिकोण के दो कोण और एक भुजा दूसरे त्रिकोण के दो कोणों और एक भुजा के बराबर हैं।
- (d) RHS परीक्षण: एक समकोण त्रिकोण की कर्ण और एक भुजा दूसरे समकोण त्रिकोण की कर्ण और एक भुजा के बराबर हैं।
➢ मध्य बिंदु प्रमेय
- किसी त्रिकोण की दो भुजाओं के मध्य बिंदुओं को जोड़ने वाली रेखा तीसरी भुजा के समानांतर होनी चाहिए और उसकी लंबाई उस (तीसरी भुजा) की आधी होनी चाहिए।
- सन्निकट त्रिकोण ABC में, यदि D और E क्रमशः भुजाओं AB और AC के मध्य बिंदु हैं, तो DE || BC और DE = ½ BC है।
➢ समान त्रिकोण
- दो आकृतियों को समान कहा जाता है, यदि उनके आकार समान हों लेकिन आकार आवश्यक नहीं है। यदि दो त्रिकोण समान हैं, तो उनके समकक्ष कोण बराबर होते हैं और समकक्ष भुजाएँ अनुपात में होती हैं।
- चित्र में: ΔABC ∼ ΔDEF तब, ∠A = ∠D, ∠B = ∠E एवं ∠C = ∠F।
त्रिकोणों की समानता के परीक्षण:
- (a) AAA समानता परीक्षण: एक त्रिकोण के तीन कोण क्रमशः दूसरे त्रिकोण के तीन समकक्ष कोणों के बराबर होते हैं।
- (b) SAS समानता परीक्षण: दो समकक्ष भुजाओं का अनुपात बराबर है और उन भुजाओं के बीच वाले कोण समान हैं।
- (c) SSS समानता परीक्षण: दोनों त्रिकोणों की तीन समकक्ष भुजाओं का अनुपात बराबर है।

➢ मूल अनुपात सिद्धांत
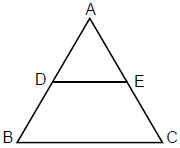
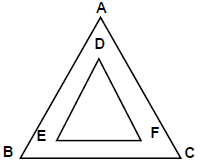
- यदि एक त्रिभुज में एक रेखा को त्रिभुज के एक पक्ष के समानांतर खींचा जाता है और वह अन्य दो पक्षों को काटती है, तो यह अन्य दो पक्षों को अनुपात में विभाजित करती है।
- यदि ΔABC में, DE को BC के समानांतर खींचा जाता है, तो यह पक्ष AB और AC को अनुपात में विभाजित करेगा।
महत्वपूर्ण परिणाम
- यदि ΔABC में DE II BC है, और A से गुजरने वाली और BC के समानांतर एक रेखा खींची जाती है, तो हमें प्राप्त होगा:
➢ समान त्रिभुजों के क्षेत्रफल
- दो समान त्रिभुजों के क्षेत्रफल का अनुपात उनके संबंधित पक्षों के वर्ग के अनुपात के समान होता है। अर्थात्, यदि ΔABC ∼ ΔDEF है, तो दो समान त्रिभुजों के क्षेत्रफल का अनुपात यह भी समान है:
- (क) उनके संबंधित मध्याओं के वर्ग का अनुपात।
- (ख) उनके संबंधित ऊँचाइयों के वर्ग का अनुपात।
- (ग) उनके संबंधित कोण बिसेक्टर के वर्ग का अनुपात।
- यदि दो त्रिभुज समान हैं, तो निम्नलिखित गुणधर्म सत्य हैं:
- (क) मध्याओं का अनुपात उनके संबंधित पक्षों के अनुपात के बराबर है।
- (ख) ऊँचाइयों का अनुपात उनके संबंधित पक्षों के अनुपात के बराबर है।
- (ग) आंतरिक बिसेक्टर का अनुपात उनके संबंधित पक्षों के अनुपात के बराबर है।
➢ कोण बिसेक्टर सिद्धांत
➢ कोण बिसेक्टर प्रमेय
- एक त्रिकोण के कोण का आंतरिक बिसेक्टर विपरीत भुजा को उस कोण को बनाने वाली भुजाओं के अनुपात में आंतरिक रूप से विभाजित करता है। उदाहरण के लिए, Δ ABC में जहाँ AD ∠A का बिसेक्टर है, तब:
➢ इंटरसेप्ट प्रमेय
➢ इंटरसेप्ट प्रमेय
- दो ट्रांसवर्सल (कटने वाली रेखाएं) द्वारा तीन या अधिक समानांतर रेखाओं पर किए गए इंटरसेप्ट अनुपात में होते हैं।
- चित्र में, रेखाएं l और m तीन समानांतर रेखाओं AB, CD, EF पर ट्रांसवर्सल हैं। तब, AC, BD और CE, DF द्वारा किए गए इंटरसेप्ट (दो समानांतर रेखाओं के बीच की लंबाई के भाग) क्रमशः अनुपात में होते हैं।
➢ पायथागोरस प्रमेय
- एक समकोण त्रिकोण की कर्ण का वर्ग अन्य दो भुजाओं के वर्गों के योग के बराबर होता है। अर्थात्, एक समकोण त्रिकोण ABC में, जो C पर समकोण है।
- पायथागोरियन त्रिवेणी: पायथागोरियन त्रिवेणी वे संख्याओं के समूह हैं जो एक समकोण त्रिकोण की तीन भुजाओं के रूप में ली जा सकती हैं। कुछ पायथागोरियन त्रिवेणी (3, 4, 5), (5, 12, 13), (7, 24, 25), (9, 40, 41) आदि हैं।

➢ तीव्र कोण प्रमेय
➢ तीव्र कोण प्रमेय
- तीव्र कोण त्रिकोण ABC में, AD, शीर्ष A से BC पर ऊँचाई है, और ∠ABC सभी तीन कोणों में सबसे बड़ा कोण है। तब:
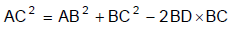
➢ obtuse कोण प्रमेय
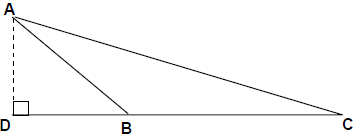
➢ obtuse कोण प्रमेय
- obtuse कोण त्रिकोण ABC में, AD, शीर्ष A से CB पर ऊँचाई है, और ∠ABC सभी तीन कोणों में सबसे बड़ा कोण है। तब AC2 = AB2 + BC2 - 2BD × BC
➢ अपोलोनियस का प्रमेय
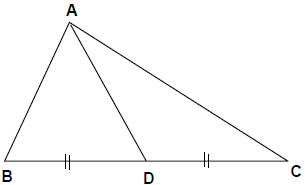
➢ अपोलोनियस का प्रमेय
- यह प्रमेय उपरोक्त दो प्रमेयों का संयोजन है और मध्य रेखा की लंबाई देता है। यदि ΔABC में, AD मध्य रेखा है, जो BC पर D पर मिलती है। तब:
|
142 videos|172 docs|185 tests
|





















