महत्वपूर्ण सूत्र: ज्यामिति | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download

परिभाषा

ज्यामिति आकारों और उनके लक्षणों के चारों ओर घूमती है। इसे दो मुख्य शाखाओं में वर्गीकृत किया जा सकता है: समतल ज्यामिति, जो रेखाओं, वृत्तों और त्रिकोणों जैसे सपाट आकारों से संबंधित है—ये ऐसे आकार हैं जिन्हें कागज पर खींचा जा सकता है; और ठोस ज्यामिति, जो तीन आयामी स्थान की ज्यामिति से संबंधित है, वह प्रकार का स्थान जिसमें हम निवास करते हैं।

परिधि

विस्तार से कहें तो, परिधि उस सीमा को संदर्भित करती है जो एक द्वि-आयामी आकार को घेरती या उसे चारों ओर से घेरती है।

मूल ज्यामिति सूत्र - क्षेत्रफल, आयतन और परिधि

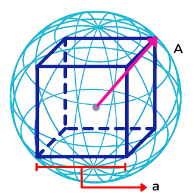
संभावित largest Sphere

इस प्रकार में आपको “a” सेंटीमीटर का एक घन दिया जाएगा और पूछा जाएगा कि इससे सबसे बड़ी संभव esfera का आयतन क्या है, जिसे इसमें से निकाला जा सकता है। Sphere का विकर्ण: a/2 = त्रिज्या घन का शेष खाली स्थान: a³ - πa³/6

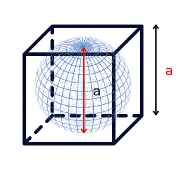
संभावित largest Cube

इस प्रकार में आपको “A” सेंटीमीटर त्रिज्या का एक esfera दिया जाएगा और पूछा जाएगा कि इससे सबसे बड़े घन का आयतन क्या है, जिसे इसमें से निकाला जा सकता है। यहाँ OA = esfera की त्रिज्या। तो, esfera का व्यास = 2a घन का विकर्ण = √3x (यदि वर्ग की भुजा x है)

सही कोण वाले त्रिकोण में सबसे बड़ा वर्ग

इस प्रकार में आपको एक वर्ग BDEF दिया जाएगा जब इसके एक कोने का मिलान त्रिकोण ABC के सही कोण के कोने से हो। वर्ग की भुजा: वर्ग का क्षेत्रफल:

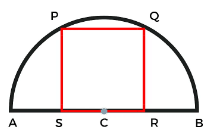
सेमि सर्कल में सबसे बड़ा वर्ग

इस प्रकार में आपसे पूछा जाएगा कि “r” त्रिज्या के सेमी सर्कल में सबसे बड़े वर्ग का क्षेत्रफल क्या है। वर्ग का क्षेत्रफल:

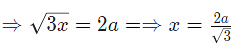
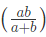
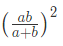
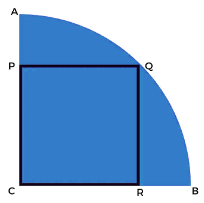
चौथाई सर्कल में अंकित सबसे बड़ा वर्ग

चौथाई सर्कल में अंकित सबसे बड़ा वर्ग

इस प्रकार के प्रश्न में आपसे एक चौथाई सर्कल के त्रिज्या “r” में अंकित सबसे बड़े वर्ग का क्षेत्रफल या भुजा पूछी जा सकती है।

• वर्ग की भुजा: r/√2
• वर्ग का क्षेत्रफल: r²/2

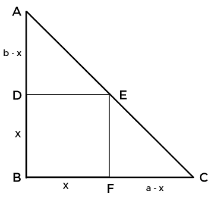
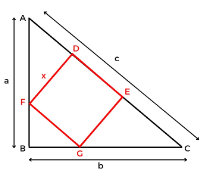
इस प्रकार के प्रश्न में आपको एक वर्ग DEGF दिया जाएगा जब इसके एक कोने का सम्मिलन त्रिभुज ABC के समकोण के कर्ण के साथ हो और आपसे वर्ग की भुजा पूछी जा सकती है।

• वर्ग की भुजा:

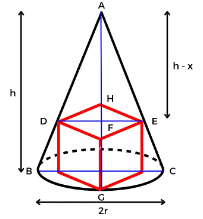
शंकु से निकाला जा सकने वाला सबसे बड़ा घन

इस प्रश्न में आपसे ऐसे घन की भुजा पूछी जाएगी जिसे एक शंकु से निकाला जाएगा जिसके ऊँचाई ‘h’ सेंटीमीटर और त्रिज्या ‘r’ सेंटीमीटर है।

• घन की भुजा:

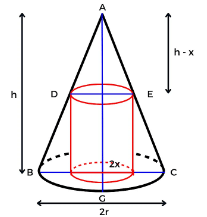
सिलेंडर का अधिकतम आयतन

इसमें आपसे ऐसे सिलेंडर का आयतन पूछी जाएगी जिसे एक समवृत्त शंकु से निकाला जा सकता है।

• सिलेंडर का अधिकतम आयतन:

उदाहरण

प्रश्न 1: रतन के पास एक कठोर लकड़ी का बोर्ड था जिससे उसने 10 सेंटीमीटर की भुजा वाला एक समभुज त्रिकोण बनाया। इसका क्षेत्रफल ज्ञात करें। उत्तर: समभुज त्रिकोण का क्षेत्रफल ज्ञात करने का सूत्र = 43.30 cm²

प्रश्न 2: सम ने मिट्टी से एक वृत्त बनाया, इसका क्षेत्रफल π के संदर्भ में ज्ञात करें, यदि वृत्त का व्यास 18 सेंटीमीटर है? उत्तर: व्यास = 18 सेंटीमीटर, त्रिज्या = 9 सेंटीमीटर, वृत्त का क्षेत्रफल = πr², क्षेत्रफल = π(9²), क्षेत्रफल = 81π cm²

प्रश्न 3: 90º का पूरक कोण क्या है? उत्तर: पूरक कोण वे होते हैं जिनका योग 180 होता है। प्रश्न के अनुसार: 90º + x = 180, अत: x = 180 - 90 = 90º

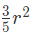
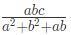
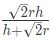
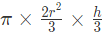
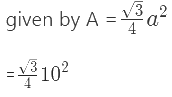
प्रश्न 4: राज ने अपने कमरे के लिए एक आईने का खरीदा जिसकी लंबाई 12 मीटर और विकर्ण 15 मीटर है, आयत का चौड़ाई ज्ञात कीजिए। उत्तर: आयत की चौड़ाई 9 मीटर है। एक आयत में, विकर्ण आयत को दो समान समकोण त्रिकोणों में विभाजित करता है। हम पायथागोरस के प्रमेय का उपयोग करके आयत की चौड़ाई (‘b’) ज्ञात कर सकते हैं, जिसका उपयोग लंबाई (‘a’) और विकर्ण (‘c’) के साथ किया जाता है:

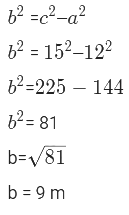
प्रश्न 5: एक आइस-क्रीम कोन का आयतन ज्ञात कीजिए जिसका त्रिज्या 6 सेमी और ऊँचाई 7 सेमी है। उत्तर: हम जानते हैं कि कोन का आयतन:

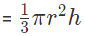
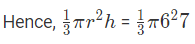
= 84π सेमी³