विस्तृत नोट्स: औसत | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download

परिचय

• यह अध्याय गणितीय योग्यता और डेटा व्याख्या अनुभागों में अधिकांश प्रश्नों का आधारभूत सिद्धांत है।
• यह एक महत्वपूर्ण अध्याय है और इस सिद्धांत में त्वरित समाधान विधियाँ आपको समय बचाने में मदद करेंगी - जो आपकी सफलता के लिए एक आवश्यक कारक है।
• आइए 2019 के प्रश्न के माध्यम से इस अध्याय से संबंधित प्रश्नों की झलक देखें। यह प्रश्न आपको यह समझने में मदद करेगा कि इस अध्याय से प्रश्न कैसे पूछे जाते हैं।

परिभाषा

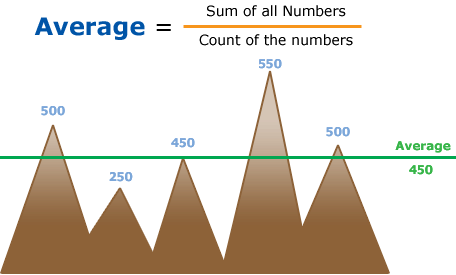
सादा औसत (या मीन) को मात्राओं के योग के अनुपात के रूप में परिभाषित किया जाता है।

यहाँ x1, x2, x3, ----------- xn उस मात्रा के n मानों का प्रतिनिधित्व करते हैं और यह मीन है। औसत या मीन को केंद्रीय प्रवृत्ति का एक माप कहा जाता है। उदाहरण: औसत सूत्र

आइए पहले पाँच प्राकृतिक संख्याओं 1, 2, 3, 4 और 5 का एक बहुत सरल उदाहरण लेते हैं:

अब चलिए इन 5 संख्याओं में 2 और 3 जोड़ते हैं:

उदाहरण 1: यदि 45 वर्ष का एक व्यक्ति 5 व्यक्तियों के एक समूह में शामिल होता है जिनकी औसत उम्र 39 वर्ष है। तो समूह की नई औसत उम्र क्या होगी?

• कुल उम्र होगी 45 + 5 × 39 = 240। और अब कुल 6 व्यक्ति होंगे। तो, औसत होगी 240/6 = 40। (या)
• चूंकि, 45, 39 से 6 अधिक है, नए व्यक्ति के शामिल होने से कुल बढ़कर 6 हो जाएगा और इसलिए औसत में 1 की वृद्धि होगी। इसलिए, औसत 39 + 1 = 40 है।

तो, औसत 39 + 1 = 40 है।

उदाहरण 2. दो छात्रों के अंक 50 और 54 हैं जो कक्षा VIII A छोड़कर कक्षा VIII B में चले जाते हैं। इसके परिणामस्वरूप, कक्षा VIII A के औसत अंक 48 से 46 पर गिर जाते हैं। कक्षा VIII A में प्रारंभ में कितने छात्र थे?

• कक्षा VIII A के सभी छात्रों का औसत 46 है, इन दो छात्रों को निकालने के बाद। उनके अंक 46 से क्रमशः 4 और 8 अधिक हैं। इसलिए, इन दो छात्रों के जुड़ने से 12 अंक और जुड़ रहे हैं, और इस प्रकार औसत 2 अंक बढ़ रहा है।
• इस कक्षा में इन दो छात्रों सहित 6 छात्र होने चाहिए। यही प्रारंभिक छात्रों की संख्या है।

उदाहरण 3. x लगातार प्राकृतिक संख्याओं का औसत N है। यदि समूह में अगली प्राकृतिक संख्या जोड़ी जाती है, तो औसत बढ़ जाता है:

(a) x पर निर्भर करता है

(b) श्रृंखला की प्रारंभिक संख्या पर निर्भर करता है

(c) दोनों (1) और (2)

(d) (e) इनमें से कोई नहीं

सही उत्तर विकल्प (d) है। लगातार संख्याओं का औसत मध्य संख्या होती है। यदि सूची में एक और संख्या जोड़ी जाती है, तो मध्य संख्या 0.5 दाईं ओर बढ़ जाती है। इसलिए उत्तर (d) है।

भारित औसत

• यदि कोई आपसे पूछता है कि कक्षा X के दोनों अनुभागों A और B के संयुक्त औसत अंक क्या हैं, जब दोनों अनुभागों के औसत अंक क्रमशः 60% और 70% हैं? तो आपका उत्तर 65% होगा, लेकिन यह गलत है क्योंकि आपको प्रत्येक अनुभाग में छात्रों की कुल संख्या नहीं पता है।
• इसलिए, भारित औसत निकालने के लिए, हमें दोनों अनुभागों में छात्रों की संख्या जानना आवश्यक है।
• मान लीजिए N1, N2, N3, …. Nn वे भार हैं जो क्रमशः परिवर्तनशील मान X1, X2, X3, …….. Xn से जुड़े हैं। फिर भारित अंकगणितीय औसत, सामान्यतः इस प्रकार व्यक्त किया जाता है: किसी भी दो भिन्न मात्राओं को भिन्न अनुपात में लिया जाने पर।
• भारित औसत एक झूले की तरह होता है। किसी मात्रा का अनुपात अधिक होने पर, औसत का झुकाव मध्य मान से उस मान की ओर अधिक होगा जिसके अधिक अनुपात हैं।

उदाहरण 4. कक्षा X के एक अनुभाग के 30 छात्रों के औसत अंक 20 हैं जबकि दूसरे अनुभाग के 20 छात्रों के औसत अंक 30 हैं। कक्षा X के पूरे वर्ग के लिए औसत अंक ज्ञात करें।

हम प्रश्न को साधारण औसत और भारित औसत विधि दोनों का उपयोग करके हल कर सकते हैं।

औसत के बारे में वास्तविक तथ्य

• यदि प्रत्येक संख्या को एक निश्चित मात्रा n से बढ़ाया/घटाया जाता है, तो औसत भी उसी मात्रा से बढ़ेगा या घटेगा।
• यदि प्रत्येक संख्या को एक निश्चित मात्रा n से गुणा/भाग किया जाता है, तो औसत भी उसी मात्रा से गुणा या भाग होगा।
• यदि आधी मात्राओं में एक ही मान जोड़ा जाता है और बाकी आधी मात्राओं से वही मान घटाया जाता है, तो औसत का अंतिम मान नहीं बदलेगा।

औसत गति

• यह कुल दूरी को यात्रा करने में लगने वाले समय से विभाजित किया जाता है।

औसत गति का सूत्र

• यदि d1 और d2 गति v1 और v2 पर तय की गई दूरी हैं और समय t1 और t2 क्रमशः हैं, तो कुल दूरी (x1 x2) पर औसत गति निम्नलिखित द्वारा दी जाती है: सुझाव: औसत गति कभी भी दो गुना या उससे अधिक नहीं हो सकती।
• यदि दोनों दूरी समान हैं, अर्थात् d1 = d2 = d, तो {यानी दो गतियों का हार्मोनिक औसत}।
• लेकिन यदि दोनों समय समान हैं, अर्थात् t1 = t2 = t, तो औसत गति = {यानी दो गतियों का बीजगणितीय औसत}।

• यदि d1 और d2 गति v1 और v2 पर तय की गई दूरी हैं और समय t1 और t2 क्रमशः हैं, तो कुल दूरी (x1 x2) पर औसत गति निम्नलिखित द्वारा दी जाती है: सुझाव: औसत गति कभी भी दो गुना या उससे अधिक नहीं हो सकती।
• यदि दोनों दूरी समान हैं, अर्थात् d1 = d2 = d, तो {यानी दो गतियों का हार्मोनिक औसत}।

उदाहरण 5: 21 से शुरू होने वाली 10 क्रमिक संख्याओं का औसत है:

औसत केवल मध्य संख्या होती है, जो 5वीं और 6वीं संख्या का औसत है, अर्थात् 25 और 26, यानी 25.5।

अगले 3 प्रश्नों के लिए निर्देश:

एक कक्षा में 60 छात्र हैं। इन छात्रों को तीन समूहों A, B, C में विभाजित किया गया है, जिसमें क्रमशः 15, 20 और 25 छात्र हैं। समूह A और C को मिलाकर समूह D का निर्माण किया गया है।