महत्वपूर्ण सूत्र: अनुपात और समानुपात | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download
प्रतियोगी परीक्षाओं में अनुपात और अनुपात का ज्ञान वास्तव में महत्वपूर्ण है। यह विचार, जो बुनियादी उच्च विद्यालय गणित से आते हैं, अंकगणित खंड में अत्यंत महत्वपूर्ण हैं और यहाँ तक कि डेटा व्याख्या जैसे अन्य भागों में भी दिखाई देते हैं। अनुपात और अनुपात में अच्छे होना केवल सहायक नहीं है; यह समान त्रिकोणों, मिश्रणों और दावों से संबंधित समस्याओं को हल करने के लिए एक सुपर उपयोगी उपकरण की तरह है। इन बुनियादी बातों को समझना केवल एक चीज को समझने के बारे में नहीं है; यह विभिन्न विषयों में प्रतियोगी परीक्षाओं के दौरान कई विभिन्न प्रश्नों को हल करने में मदद करने वाला एक कुंजी की तरह है।
परिचय
अनुपात और अनुपात को मुख्य रूप से अंशों के आधार पर समझाया जाता है। जब एक अंश को a:b के रूप में प्रस्तुत किया जाता है, तो इसे अनुपात कहा जाता है जबकि अनुपात यह बताता है कि दो अनुपात समान हैं।
- यहाँ, a और b कोई भी दो पूर्णांक हैं। अनुपात और अनुपात दो महत्वपूर्ण अवधारणाएँ हैं, और यह गणित और विज्ञान में विभिन्न अवधारणाओं को समझने की नींव है। अनुपात और अनुपात को एक ही सिक्के के दो पहलुओं के रूप में कहा जाता है। जब दो अनुपात का मान समान होता है, तो उन्हें अनुपात में कहा जाता है। सरल शब्दों में, यह दो अनुपातों की तुलना करता है।
- अनुपात को ‘::’ या ‘=’ प्रतीक द्वारा दर्शाया जाता है।
- सरल शब्दों में, विभाजन द्वारा दो मात्राओं की तुलना को अनुपात कहा जाता है और दो अनुपातों की समानता को अनुपात कहा जाता है। एक अनुपात को विभिन्न रूपों में जैसे x : y या x/y में लिखा जा सकता है और इसे सामान्यतः इस तरह पढ़ा जाता है, x is to y। दूसरी ओर, अनुपात एक समीकरण है जो कहता है कि दो अनुपात समान हैं। एक अनुपात को x : y : : z : w के रूप में लिखा जाता है, और इसे इस तरह पढ़ा जाता है, x is to y as z is to w। यहाँ, x/y = z/w जहाँ w और y 0 के बराबर नहीं हैं।
अनुपात क्या है?

अनुपात समान प्रकार की मात्राओं की तुलना है, यह एक अमूर्त मात्रा है और इसका कोई इकाई नहीं होता है।
- दो मात्राओं a और b का अनुपात, जो समान इकाइयों में हो, वह a/b का भिन्न होता है और इसे हम a: b के रूप में लिखते हैं, जो a/b के बराबर होता है।
- अनुपात a: b में, पहले पद को हम पूर्वपद और b को उपरपद कहते हैं।
- उदाहरण 1: अनुपात 5 : 9, 5/9 का प्रतिनिधित्व करता है जिसमें पूर्वपद = 5, उपरपद = 9 है।
- उदाहरण 2: यदि हम अनुपात के प्रत्येक पद को एक ही संख्या (जो शून्य नहीं है) से गुणा और भाग करते हैं, तो इससे अनुपात पर कोई प्रभाव नहीं पड़ता जैसे कि 5:9 = 10:18 = 15:27।
अनुपात के महत्वपूर्ण गुण
1. यदि पूर्वपद और उपरपद को एक ही गैर-शून्य संख्या से गुणा या भाग किया जाए, तो अनुपात वही रहता है,
- a/b = pa/pb = qa/qb , जहाँ p, q ≠ 0
- a/b = (a/p) / (b/p) = (a/q) / (b/q) , जहाँ p, q ≠ 0
2. दो अनुपातों को उनके भिन्न संकेत में इस प्रकार तुलना की जा सकती है जैसे हम वास्तविक संख्याओं की तुलना करते हैं।
- a/b = p/q ⟺ aq = bp
- a/b > p/q ⟺ aq > bp
- a/b < p/q="" ⟺="" aq="" />< />
3. यदि दो अनुपात a/b और c/d समान हैं
- a/b = c/d ⟹ b/a = d/c (Invertendo)
- a/b = c/d ⟹ a/c = b/d (Alternendo)
- a/b = c/d ⟹ (ab)/b = (cd)/d (Componendo)
- a/b = c/d ⟹ (a-b)/b = (c-d)/d (Dividendo)
4. अनुपात के बारे में याद रखने योग्य मुख्य बिंदु:
अनुपात की परिभाषा:
- समान प्रकार की मात्राओं के बीच अनुपात होना चाहिए।
- दो चीजों की तुलना करते समय, इकाइयाँ समान होनी चाहिए।
- शब्दों का एक महत्वपूर्ण क्रम होना चाहिए।
- यदि अनुपात समान हों, तो दो अनुपातों की तुलना की जा सकती है, जैसे भिन्न।
अनुपातों के प्रकार
1. यौगिक अनुपात:
अनुपातों का यौगिक अनुपात: (a : b), (c : d), (e : f) है (ace : bdf)
2. गुणांक अनुपात:
- (a : b) का गुणांक अनुपात (a2 : b2) है।
- (a : b) का उप-गुणांक अनुपात (√a : √b) है।
- (a : b) का त्रैतीयक अनुपात (a3 : b3) है।
- (a : b) का उप-त्रैतीयक अनुपात (a1/3 : b1/3) है।
- यदि a/b = c/d, तो a b/a - b = c d/c - d [यौगिक और लाभ]
अनुपात क्या है?
दो अनुपातों की समानता को अनुपात कहते हैं, अर्थात यदि a/b = c/d, तो a, b, c, d को अनुपात में कहा जाता है।
- यदि a : b = c : d, तो हम लिखते हैं a : b :: c : d और कहते हैं कि a, b, c, d अनुपात में हैं।
- यहां a और d को अंतिम कहा जाता है, जबकि b और c को माध्य कहा जाता है।
माध्य का गुणनफल = अंतिम का गुणनफल
इस प्रकार, a : b :: c : d ⇔ (b x c) = (a x d)

अनुपात के महत्वपूर्ण गुण
यदि a:b = c:d एक अनुपात है, तो:
- अंतिम का गुणनफल = माध्य का गुणनफल, अर्थात ad = bc।
- b, c, d,… यदि निरंतर अनुपात में हैं, तो a:b = b:c = c:d।
- यदि a:b = b:c है, तो b को माध्य अनुपात कहा जाता है और b2 = ac।
- दो संख्याओं a और b का तीसरा अनुपात c है, ऐसा कि a:b = b:c।
- a, b, c के लिए d चौथा अनुपात है यदि a:b = c:d।
अनुपात और अनुपात के बीच का अंतर
अनुपात और अनुपात का सिद्धांत समझने के लिए, यहां दिए गए अनुपात और अनुपात के बीच का अंतर जानें।
| क्र.सं. | अनुपात | अनुपात |
|---|---|---|
| 1 | अनुपात का उपयोग समान इकाई के दो वस्तुओं के आकार की तुलना करने के लिए किया जाता है। | अनुपात का उपयोग दो अनुपातों के संबंध को व्यक्त करने के लिए किया जाता है। |
| 2 | इसे कोलन (:) या स्लैश (/) का उपयोग करके व्यक्त किया जाता है। | इसे डबल कोलन (::) या समानता के प्रतीक (=) का उपयोग करके व्यक्त किया जाता है। |
| 3 | यह एक अभिव्यक्ति है। | यह एक समीकरण है। |
| 4 | समस्या में अनुपात की पहचान के लिए कुंजी शब्द "प्रत्येक के लिए" है। | समस्या में अनुपात की पहचान के लिए कुंजी शब्द "में से" है। |
अनुपात और अनुपात के प्रश्नों को हल करने के लिए सरल विधि
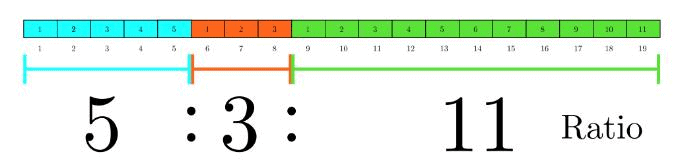
जब हमें कई अनुपातों में से अनुपात प्राप्त करना होता है, तो LCM प्रक्रिया बहुत जटिल हो जाती है। इसके लिए हमारे पास किसी भी लंबाई की अनुपात श्रृंखला के लिए निम्नलिखित सरल विधि है।
मान लीजिए आपके पास अनुपात इस प्रकार है:
⇨ A : B = 1 : 2
⇨ B : C = 2 : 3
⇨ C : D = 5 : 6
⇨ D : E = 7 : 8
यदि हमें A : B : C : D : E ज्ञात करना होता, तो LCM विधि में काफी समय लगता, जो सीमित घंटों की परीक्षाओं में संभव नहीं है।
संक्षिप्त विधि इस प्रकार है:
A : B : C : D : E को सीधे इस प्रकार लिखा जा सकता है:
⇨ 1 × 2 × 5 × 7 : 2 × 2 × 5 × 7 : 2 × 3 × 5 × 7 : 2 × 3 × 6 × 7 : 2 × 3 × 6 × 8
⇨ 70 : 140 : 210 : 252 : 288
इस मामले के लिए विचार प्रक्रिया इस प्रकार है: A : B, B : C, C : D, और D : E से A : B : C : D : E का संयुक्त अनुपात प्राप्त करना।
- A सभी अंशों के गुणनफल के अनुरूप होगा (1 × 2 × 5 × 7)।
- B पहले हर को और अंतिम 3 अंशों को लेगा (2 × 2 × 5 × 7)।
- C पहले दो हर और अंतिम 2 अंशों को लेगा (2 × 3 × 5 × 7)।
- D पहले 3 हर और अंतिम अंश को लेगा (2 × 3 × 6 × 7) और E सभी चार हरों को लेगा (2 × 3 × 6 × 8)।
अनुपात और अनुपात के उपाय
अनुपात और अनुपात: महत्वपूर्ण सूत्र
- यदि u/v = x/y, तो uy = vx
- यदि u/v = x/y, तो u/x = v/y
- यदि u/v = x/y, तो v/u = y/x
- यदि u/v = x/y, तो (u v)/v = (x y)/y
- यदि u/v = x/y, तो (u-v)/v = (x-y)/y
- यदि u/v = x/y, तो (u v)/ (u-v) = (x y)/(x-y), जिसे Componendo-Dividendo Rule कहा जाता है
- यदि a/(b c) = b/(c a) = c/(a b) और a b c ≠ 0, तो a = b = c
अनुपात सूत्र: a : b ⇒ a/b
अनुपात सूत्र: a/b = c/d या a : b :: c : d
चौथा, तीसरा और औसत अनुपात: यदि a : b = c : d, तो:
- d, a, b, c के लिए चौथा अनुपात है।
- c, a और b के लिए तीसरा अनुपात है।
- a और b के बीच का औसत अनुपात √(ab) है।
1. अनुपात:
- अनुपात केवल समान प्रकार की दो मात्राओं का सरल रूप है या तुलना है। एक अनुपात एक संख्या है, जो एक मात्रा को दूसरी मात्रा के अंश के रूप में दर्शाता है। उदाहरण: दो संख्याओं का अनुपात 5 से 6 है, जो 5:6 है। यह यह भी व्यक्त करता है कि एक मात्रा कितनी बार दूसरी मात्रा के बराबर है। "शर्तें" वे संख्याएँ हैं जो अनुपात बनाती हैं। अनुपात का ऊपरी भाग (संख्यात्मक) को पूर्ववत कहा जाता है और भिन्न का निचला भाग (हर) को उत्तरवत या अवरोही कहा जाता है। उदाहरण: यदि अनुपात 4:6 है, तो 4 को पूर्ववत कहा जाता है और 6 को उत्तरवत कहा जाता है।
2. अनुपात:
अनुपात को '::' या '=' के रूप में दर्शाया जाता है। यदि अनुपात x:y अनुपात a:b के बराबर है, तो x, y, a, b अनुपात में हैं। इसे हम निम्नलिखित प्रतीकों का उपयोग करके दर्शाते हैं: x:y=a:b या x:y:: a:b। जब चार अंश अनुपात में होते हैं, तो दो मध्य मानों (अर्थात, 2nd और 3rd मान) का गुणनफल दो बाहरी मानों (अर्थात, 1st और 4th मान) के गुणनफल के बराबर होना चाहिए।
3. चौथा अनुपात:
- यदि x:y = a:b, तो b को x, y और a का चौथा अनुपात कहा जाता है।
- तीसरा अनुपात: यदि x:y = a:b, तो a को x, y और b का तीसरा अनुपात कहा जाता है।
- मध्यम अनुपात: x और y के बीच का मध्यम अनुपात √(xy) है।
4. अनुपात की तुलना
- हम परिभाषित करते हैं कि x:y>a:b यदि और केवल यदि x/y>a/b।
- संयुक्त अनुपात: दो अनुपातों का संयुक्त अनुपात: (x:y), (a:b), (c:d) है (xac:ybd)।
5. डुप्लिकेट अनुपात
- (x:y) का डुप्लिकेट अनुपात है ((square(x):square(y)))।
- (x:y) का उप-डुप्लिकेट अनुपात है ((root(x):root(y)))।
- (x:y) का त्रैतीयक अनुपात है ((cube(x):cube(y)))।
- (x:y) का उप-त्रैतीयक अनुपात है ((cuberoot(x):cuberoot(y)))।
- कम्पोनडिंग और डिविडेंड नियम: यदि x/y=a/b, तो x=y/x-y = a b/a-b।
6. विभाजन
- हम परिभाषित करते हैं कि a, b के लिए सीधे अनुपात में है, यदि a=kb किसी स्थायी k के लिए और हम इसे इस प्रकार लिखते हैं – a, b के अनुपात में है।
- हम कहते हैं कि a, b के लिए अप्रत्यक्ष अनुपात में है, यदि ay=b किसी स्थायी k के लिए और हम इसे इस प्रकार लिखते हैं – a, 1/b के अनुपात में है।
हल किए गए प्रश्न
प्रश्न 1: एक पुस्तकालय में, कहानी की पुस्तकों और गैर-कहानी की पुस्तकों का अनुपात 4:3 था और कहानी की कुल संख्या 1248 थी। जब कुछ और कहानी की पुस्तकें खरीदी गईं, तो अनुपात 5:3 हो गया। खरीदी गई कहानी की पुस्तकों की संख्या ज्ञात करें।
उत्तर: विकल्प ए व्याख्या:
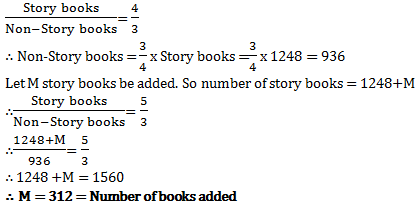
प्रश्न 2: Rs. 8400 को A, B, C और D के बीच इस प्रकार विभाजित किया गया है कि A और B, B और C, और C और D के हिस्से का अनुपात क्रमशः 2:3, 4:5 और 6:7 है। A का हिस्सा क्या है?
उत्तर: विकल्प ए व्याख्या:

प्रश्न 3: पिता की वर्तमान आयु और पुत्र की वर्तमान आयु का अनुपात 7:2 है। 10 वर्ष बाद उनकी आयु का अनुपात 9:4 होगा। पिता की वर्तमान आयु क्या है?
उत्तर: विकल्प ए
व्याख्या:

प्रश्न 4: अजय और राज के पास मिलाकर Rs. 1050 हैं। यदि अजय Rs. 150 लेता है, तो अजय के पास वही राशि होगी जो पहले राज के पास थी। अजय और राज के पास प्रारंभ में राशि का अनुपात ज्ञात करें।
उत्तर: विकल्प डी व्याख्या:

प्रश्न 5: P, Q, और R प्रकार के प्रत्येक लेख की कीमत क्रमशः Rs. 300, Rs. 180 और Rs. 120 है। सुरेश ने Rs. 6480 में प्रत्येक प्रकार के लेखों को 3:2:3 के अनुपात में खरीदा। उसने प्रकार Q के कितने लेख खरीदे?
a. 8
उत्तर: विकल्प ए व्याख्या:

प्रश्न 6: Rs. 60 को Mike और John के बीच 1:2 के अनुपात में विभाजित करें।
हल: मान लीजिए Mike का भाग x है।
फिर John का भाग 2x है।
इस प्रकार, x + 2x = 60
3x = 60
x = (60/3)
x = 20।
इसलिए, Mike का भाग = x = Rs. 20
John का भाग = 2x = Rs. (2*20) = Rs. 40
प्रश्न 7: तीन बर्तनों में अल्कोहल और पानी का अनुपात क्रमशः 3:5, 1:3, और 1:1 है। यदि सभी तीन समाधानों को मिलाया जाए, तो अंतिम समाधान में अल्कोहल और पानी का अनुपात क्या होगा?
समाधान: यहाँ हमें तीन जारों में घोल की मात्राएँ नहीं दी गई हैं। केवल शराब और पानी का अनुपात दिया गया है। यदि घोल की मात्रा का अनुपात दिया गया होता, तो हम अंतिम घोल में शराब और पानी का अनुपात निर्धारित कर सकते थे। इसलिए, यहाँ उत्तर "निर्धारित नहीं किया जा सकता" होगा।
प्रश्न 8: यदि एक थैले में एक-रुपये, 50-पैसे और 25-पैसे के सिक्कों के रूप में 495 रुपये हैं, जो अनुपात 1:8:16 में हैं। थैले में कितने 50 पैसे के सिक्के हैं?
समाधान: मान लें, आपके पास x संख्या में एक रुपये के सिक्के हैं। अब सिक्के अनुपात 1:8:16 में हैं। इसका मतलब है कि यदि हमारे पास x संख्या में एक रुपये के सिक्के हैं, तो हमारे पास 50 पैसे के 8x सिक्के और 25 पैसे के 16x सिक्के होंगे। यहाँ प्रश्न में दिए गए अनुपात का क्रम बहुत महत्वपूर्ण है। इस मामले में, क्रम एक रुपये, 50 पैसे और 25 पैसे है और अनुपात 1:8:16 है। इसलिए,
50-पैसे के सिक्कों की संख्या = 8x
25-पैसे के सिक्कों की संख्या = 16x
अब, थैले में कुल पैसे = 495 रुपये
- x (8x/2) (16x/4) = 495
(50 पैसे के सिक्कों को रुपये में बदलने के लिए 2 से विभाजित किया गया है और 25 पैसे के सिक्कों को रुपये में बदलने के लिए 4 से विभाजित किया गया है)
- 9x = 495
- x = 495/9
- x = 55
इस प्रकार, 50 पैसे के सिक्कों की संख्या = 55*8 = 440
|
142 videos|172 docs|185 tests
|
















