सारांश: मापन | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download

मेनसुरेशन

गणित का एक भाग जो विभिन्न ज्यामितीय आकृतियों के लंबाई, वॉल्यूम या क्षेत्रफल के बारे में जानकारी प्रदान करता है, उसे मेनसुरेशन कहते हैं। ये आकृतियाँ दो आयामों या तीन आयामों में होती हैं।

गणित में 3D मेनसुरेशन - महत्वपूर्ण शब्दावली

आइए विभिन्न ज्यामितीय आकृतियों से संबंधित कुछ और परिभाषाएँ जानें।

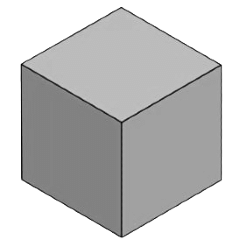
घन (Cube) के गुण

• सभी पक्ष समान हैं।
• घन के सभी छह चेहरे चौकोर आकार के होते हैं।
• हर चेहरा अन्य चार चेहरों से मिलता है।
• एक-दूसरे के विपरीत किनारे समानांतर होते हैं।
• पार्श्व = a

घन का सूत्र:

• वॉल्यूम = a³
• सतह क्षेत्र = 6a²
• तिर्यक =

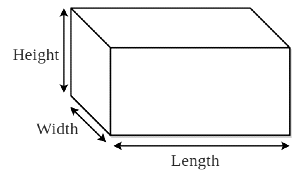
घनाभ (Cuboid) के गुण

• तीन आयामी आकृति जिसमें लंबाई, चौड़ाई और ऊँचाई होती है।
• हर चेहरा अन्य चार चेहरों से मिलता है।
• एक-दूसरे के विपरीत किनारे समानांतर होते हैं।
• ऊँचाई = h, लंबाई = l और चौड़ाई = b

घनाभ का सूत्र:

• वॉल्यूम = l × b × h
• वॉल्यूम = आधार का क्षेत्रफल × ऊँचाई
• सतह क्षेत्र = 2(lb + bh + hl)
• तिर्यक = √(l² + b² + h²)
• चार दीवारों का क्षेत्रफल = आधार का परिमाप × ऊँचाई = 2(l + b) × h
• धातु का वॉल्यूम = बाह्य वॉल्यूम – आंतरिक वॉल्यूम

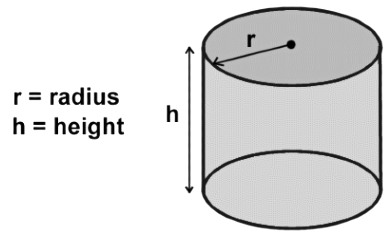
सिलेंडर (Cylinder) के गुण

• सिलेंडर में एक वक्र पक्ष होता है।
• सिलेंडर के दो ऊर्ध्वाधर सपाट अंत होते हैं जो वृत्ताकार होते हैं।

सिलेंडर का सूत्र:

• वॉल्यूम = πr²h
• सतह क्षेत्र = 2πrh
• कुल सतह क्षेत्र = 2πr(h + r)

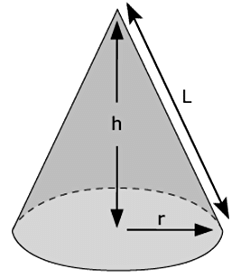
कों (Cone) के गुण

• ऊँचाई = h, तिरछी ऊँचाई = l और व्यास = r
• इसमें केवल एक शीर्ष बिंदु होता है।
• इसका आधार वृत्ताकार होता है।

कों का सूत्र:

• वॉल्यूम = (1/3)πr²h
• सतह क्षेत्र = πr(l + r)

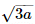
घन के गुण

• आयतन = (1/3)πr²hl
• सतह क्षेत्र = πrl
• कुल सतह क्षेत्र = πr(l + r)

गेंद के गुण

• आयतन = (4/3)πR³
• सतह क्षेत्र = 4πR²
• धातु का आयतन = (4/3)π(R³−r³)
• खोखली गेंद का आयतन = (4/3)π(R−a)³
• यहाँ, R = बाहरी त्रिज्या, r = आंतरिक त्रिज्या, a = दीवार की पतलापन

अर्धगोल के गुण

• आयतन = (2/3)πr³
• सतह क्षेत्र = 2πr²
• कुल सतह क्षेत्र = 3πr²

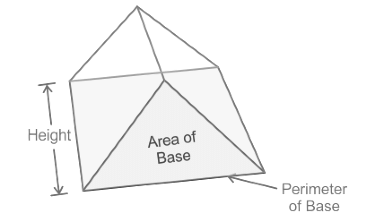
पिरामिड के गुण

• आयतन = आधार का क्षेत्रफल × ऊँचाई
• पार्श्व सतह क्षेत्र = आधार की परिधि × ढलान की ऊँचाई
• कुल सतह क्षेत्र = आधार की परिधि × ढलान की ऊँचाई + आधार का क्षेत्रफल

मापन के 3D सूत्र

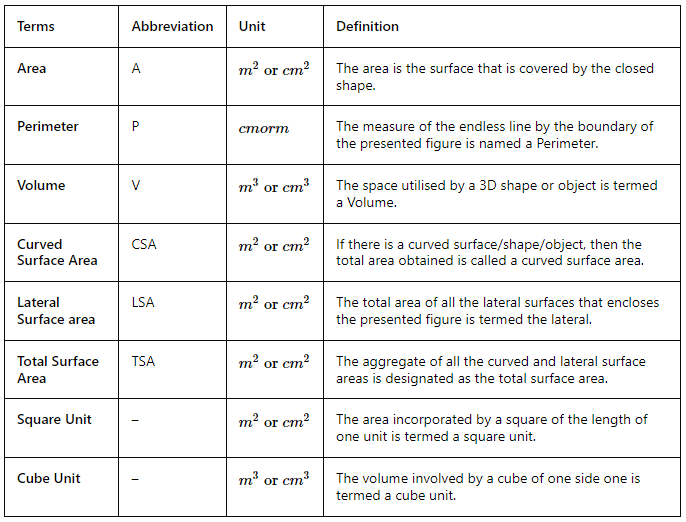
3D आकृतियों के शर्तों, गुणों और सूत्रों के ज्ञान के साथ, आइए कुछ महत्वपूर्ण सूत्रों का सारांश नीचे दी गई तालिका में प्रस्तुत करते हैं। ये मापन सूत्र मापन समस्याओं को हल करते समय बहुत उपयोगी होते हैं।

यहाँ कुछ और 3D आकृतियाँ उनके सूत्रों और चित्रों के साथ हैं।

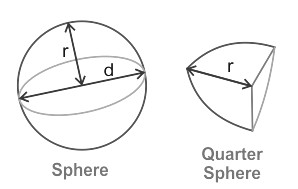
चौथाई गेंद

चौथाई गेंद एक पूर्ण गेंद का विशेष रूप से एक-चौथाई हिस्सा है। अर्थात, यदि हम एक गेंद को चार समान भागों में काटते हैं, तो प्रत्येक भाग को चौथाई गेंद कहा जाता है। इसलिए, चौथाई गेंद का आयतन एक गेंद के आयतन का एक-चौथाई है।

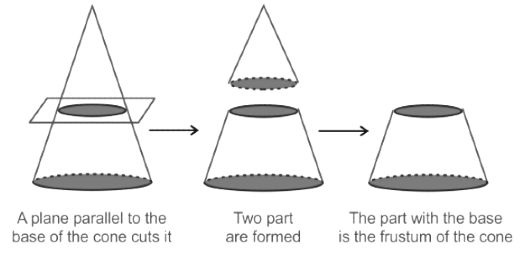
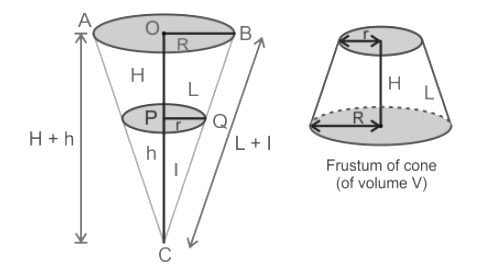
कोन का फ्रस्टम

कोन का फ्रस्टम वह खंड है जो कोन के शीर्ष बिंदु के बिना होता है जब दिए गए कोन को एक समांतर विमान से दो टुकड़ों में विभाजित किया जाता है।

कोन का फ्रस्टम अक्सर कटे हुए कोन के रूप में भी जाना जाता है। किसी अन्य 3D आकृति या वस्तु के समान, कोन का फ्रस्टम भी सतह क्षेत्र और आयतन रखता है। इसके लिए सूत्र निम्नलिखित हैं:

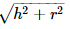
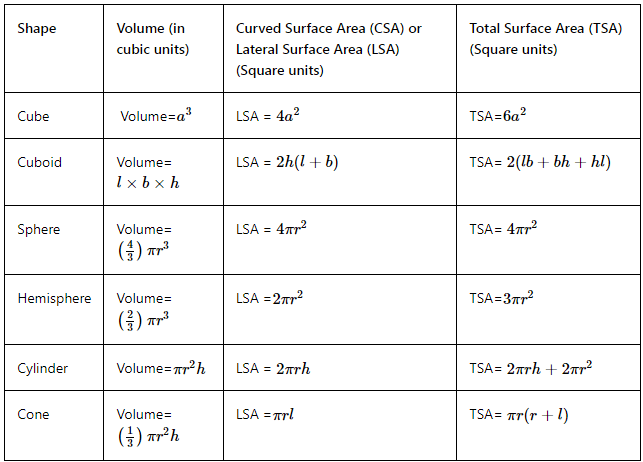
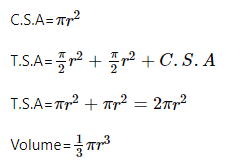
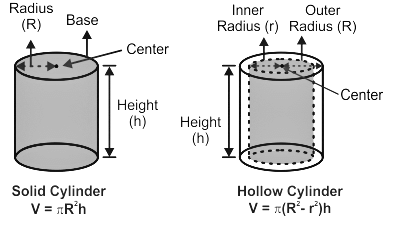
खोखला सिलिंडर (खोखला दायरा सिलिंडर)

एक खोखले सिलिंडर का आयतन को उसके द्वारा समाहित 3D स्थान के रूप में परिभाषित किया जाता है। उदाहरण के लिए, कांच का आयतन उसके अंदर उपलब्ध क्षेत्र को दर्शाता है। दूसरे शब्दों में, हम कह सकते हैं कि आयतन उस अधिकतम स्थान का प्रतिनिधित्व करता है जिसे पानी से भरा जा सकता है यदि पानी कांच में डाला जाए। यहां आधार का आंतरिक त्रिज्या ‘r’, बाह्य त्रिज्या ‘R’ और खोखले दायरा सिलिंडर की ऊँचाई ‘h’ है।

• आयतन = πh(R²−r²)
• वक्र सतह क्षेत्र = 2πRh
• कुल सतह क्षेत्र = 2πH(R + r) = 2π(R²−r²)

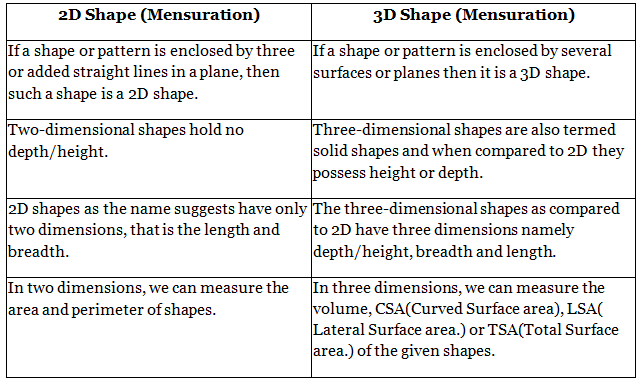
मेनसुरेशन 3D और 2D आकृतियों के बीच भिन्नताएँ

मेनसुरेशन 2D और 3D आकृतियों के बीच के अंतर को देखें।

मेनसुरेशन 3D पर प्रश्न हल करने के लिए सुझाव और तरकीबें

• टिप # 1: सुनिश्चित करें कि आप ऊपर बताए गए सभी गुणों और सूत्रों को याद रखें ताकि इस खंड से संबंधित प्रश्नों को जल्दी हल किया जा सके।
• टिप # 2: अपने मेनसुरेशन 3D के अवधारणाओं को ताज़ा करने के लिए मॉक और क्विज़ का प्रयास करें।

मेनसुरेशन 3D के उदाहरण प्रश्न

प्रश्न 1: यदि एक घन का आयतन 4913 cm³ है, तो कुल सतह क्षेत्र ज्ञात करें।

हल 1: आयतन = a³ ⇒ a³ = 4913 ∴ a = 17 cm ⇒ कुल सतह क्षेत्र = 6a² ∴ कुल सतह क्षेत्र = 6 × 17² = 1734 cm²

प्रश्न 2: यदि तीन भुजाओं का योग 45 cm है और एक घनाभ में विकर्ण की लंबाई 21 cm है, तो इस घनाभ का कुल सतह क्षेत्र ज्ञात करें।

हल 2: l + b + h = 45 ———— (1) ⇒ विकर्ण = √(l² + b² + h²) ⇒ l² + b² + h² = 21² ⇒ l² + b² + h² = 441 ———— (2) ∴ (1) से, ⇒ (l + b + h)² = 45² ⇒ l² + b² + h² + 2(lb + bh + hl) = 2025 ⇒ 441 + 2(lb + bh + hl) = 2025 ⇒ 2(lb + bh + hl) = 2025 – 441 = 1584 cm² ∴ इस घनाभ का सतह क्षेत्र 1584 cm² है।

प्रश्न 3: एक ठोस दाएं प्रिज्म का आधार एक त्रिकोण है जिसकी भुजाएँ 9 cm, 12 cm और 15 cm हैं। प्रिज्म की झुकी हुई ऊँचाई 5 cm है, प्रिज्म का कुल सतह क्षेत्र ज्ञात करें।

हल 3: आधार का परिमाप = 9 + 12 + 15 = 36 cm, आधार का क्षेत्र = ½ × 12 × 9 = 54 cm² ⇒ कुल सतह क्षेत्र = आधार का परिमाप × झुकी हुई ऊँचाई + 2 × आधार का क्षेत्र = (36 × 5) + 2 × 54 ∴ कुल सतह क्षेत्र = 288 cm²।

प्रश्न 4: दो घनों की भुजा 6 cm है जिन्हें मिलाकर एक घनाभ बनाया गया है। घनाभ का कुल सतह क्षेत्र ज्ञात करें।

हल 4: दिया गया, जब दो घन एक दूसरे के अंत में जुड़े होते हैं, तब;

• घनाभ की लंबाई = 6 + 6 = 12 cm
• घनाभ की चौड़ाई = 6 cm
• घनाभ की ऊँचाई = 6 cm

घनाभ का कुल सतह क्षेत्र = 2(lb + bh + hi) = 2(12 × 6 + 6 × 6 + 6 × 12) = 2(72 + 36 + 72) = 2(180) = 360 cm²।

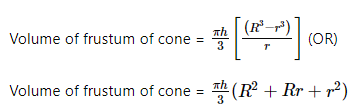
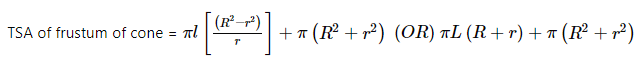
प्रश्न 3: एक ठोस समकोणीय प्रिज्म का आधार एक त्रिकोण है, जिसके भुजाएँ 9 सेमी, 12 सेमी और 15 सेमी हैं। प्रिज्म की झुकी हुई ऊँचाई 5 सेमी है। प्रिज्म का कुल सतह क्षेत्रफल ज्ञात कीजिए।

समाधान 3:

• आधार का परिमाप = 9 + 12 + 15 = 36 सेमी
• आधार का क्षेत्रफल = ½ × 12 × 9 = 54 सेमी²
• कुल सतह क्षेत्रफल = आधार का परिमाप × झुकी हुई ऊँचाई + 2 × आधार का क्षेत्रफल
• कुल सतह क्षेत्रफल = (36 × 5) + 2 × 54
• ∴ कुल सतह क्षेत्रफल = 180 + 108 = 288 सेमी²

प्रश्न 4: दो 6 सेमी किनारे वाले घन को जोड़कर एक आयताकार ठोस बनाया गया है। आयताकार ठोस का कुल सतह क्षेत्रफल ज्ञात कीजिए।

समाधान 4:

• दी गई जानकारी: जब दो घन एक के बाद एक जोड़े जाते हैं, तब;
• आयताकार ठोस की लंबाई = 6 + 6 = 12 सेमी
• आयताकार ठोस की चौड़ाई = 6 सेमी
• आयताकार ठोस की ऊँचाई = 6 सेमी
• आयताकार ठोस का कुल सतह क्षेत्रफल = 2 (लंबाई × चौड़ाई + चौड़ाई × ऊँचाई + ऊँचाई × लंबाई)
• कुल सतह क्षेत्रफल = 2(12 × 6 + 6 × 6 + 6 × 12)
• कुल सतह क्षेत्रफल = 2(72 + 36 + 72) = 2(180) = 360 सेमी²