महत्वपूर्ण सूत्र: ज्यामिति और मापन | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download
ज्यामिति और मापन प्रतियोगी परीक्षाओं में महत्वपूर्ण महत्व रखते हैं, जिससे यह उम्मीदवारों के लिए एक महत्वपूर्ण विषय बन जाता है। यह दस्तावेज़ ज्यामिति और मापन के लिए आवश्यक सूत्रों को प्रदान करके एक मूल्यवान संसाधन के रूप में कार्य करता है। इसका उद्देश्य त्वरित और प्रभावी पुनरावलोकन को सरल बनाना है, यह सुनिश्चित करते हुए कि उम्मीदवार महत्वपूर्ण अवधारणाओं को समझने में मदद कर सकें और प्रतियोगी परीक्षाओं की तैयारी में अपने ज्ञान को मजबूत कर सकें।
1. रेखाएँ और कोण
- स्ट्रेट लाइन में कोणों का योग 180° है।
- वर्टिकली विपरीत कोण समान होते हैं (बराबर)।
- यदि कोई बिंदु एक खंड के अंत बिंदुओं से समान दूरी पर है, तो यह लम्बवत बिसेक्टर पर होना चाहिए।
- जब दो समानांतर रेखाएँ एक ट्रांसवर्सल द्वारा काटी जाती हैं, तो संबंधित कोण समान होते हैं, वैकल्पिक कोण समान होते हैं और सह-आंतरिक कोण पूरक होते हैं। (सभी तीव्र कोण एक दूसरे के बराबर हैं और सभी obtuse कोण एक दूसरे के बराबर हैं)
EduRev की टिप: तीन समानांतर रेखाओं को काटने वाली ट्रांसवर्सल द्वारा बनाए गए इंटरसेप्ट्स का अनुपात किसी अन्य ट्रांसवर्सल द्वारा बनाए गए संबंधित इंटरसेप्ट्स के अनुपात के बराबर होता है। ⇒ a/b = c/d = e/f
2. त्रिकोण
- एक त्रिकोण के आंतरिक कोणों का योग 180° और बाहरी कोणों का योग 360° है।
- बाहरी कोण = दूर के आंतरिक कोणों का योग।
- दो पक्षों का योग हमेशा तीसरे पक्ष से बड़ा होता है और दो पक्षों का अंतर हमेशा तीसरे पक्ष से छोटा होता है।
- सबसे बड़े कोण के विपरीत पक्ष सबसे लंबा होता है और सबसे छोटे कोण के विपरीत पक्ष सबसे छोटा होता है।
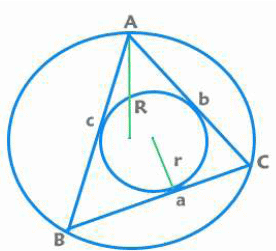
- त्रिकोण का क्षेत्रफल: = ½ x आधार x ऊँचाई = ½ x पक्षों का गुणनफल x शामिल कोण का साइन = यहाँ s अर्ध परिमाप है [s = (a + b + c)/2] = r x s [r सम्मिलित वृत्त का त्रिज्या] [R परिक्रमण वृत्त का त्रिज्या]
- एक त्रिकोण का माध्यिका एक रेखांश है जो एक शीर्ष को विपरीत पक्ष के मध्य बिंदु से जोड़ता है। तीन माध्यिकाएँ एक बिंदु पर मिलती हैं, जिसे त्रिकोण का केंद्रीय बिंदु कहा जाता है। केंद्रीय बिंदु माध्यिका को 2:1 के अनुपात में विभाजित करता है।
- त्रिकोण की ऊँचाई एक सीधी रेखा है जो एक शीर्ष के माध्यम से गुजरती है और विपरीत पक्ष या विपरीत पक्ष के विस्तार के प्रति लम्बवत होती है। तीन ऊँचाइयाँ एक बिंदु पर मिलती हैं, जिसे त्रिकोण का ऑर्थोकेंटर कहा जाता है।
- एक लम्बवत बिसेक्टर एक रेखा है जो त्रिकोण के एक पक्ष के साथ एक समकोण बनाती है और उस पक्ष को उसके मध्य बिंदु पर काटती है।
- तीन लम्बवत बिसेक्टर्स एक बिंदु पर मिलते हैं, जिसे त्रिकोण का परिक्रमण केंद्र कहा जाता है। यह परिक्रमण वृत्त का केंद्र होता है जो त्रिकोण के सभी शीर्षों से गुजरता है।
- एक कोण बिसेक्टर एक रेखा है जो किसी भी शीर्ष पर कोण को दो समान भागों में विभाजित करती है।
- तीन कोण बिसेक्टर्स एक बिंदु पर मिलते हैं, जिसे त्रिकोण का इंसेंटर कहा जाता है। यह सम्मिलित वृत्त का केंद्र है जो त्रिकोण के सभी पक्षों को छूता है।
EduRev की टिप: केंद्रीय बिंदु और इंसेंटर हमेशा त्रिकोण के भीतर होते हैं।
- (i) तीव्र कोण वाले त्रिकोण के लिए, परिक्रमण केंद्र और ऑर्थोकेंटर त्रिकोण के भीतर होते हैं।
- (ii) obtuse कोण वाले त्रिकोण के लिए, परिक्रमण केंद्र और ऑर्थोकेंटर त्रिकोण के बाहर होते हैं।
- (iii) समकोण त्रिकोण के लिए, परिक्रमण केंद्र लम्बवत की मध्य बिंदु पर होता है और ऑर्थोकेंटर उस शीर्ष पर होता है जहाँ कोण 90° है।
ऑर्थोकेंटर, केंद्रीय बिंदु और परिक्रमण केंद्र हमेशा एक ही रेखा पर होते हैं, जिसे यूलेर रेखा कहा जाता है।
- (i) ऑर्थोकेंटर केंद्रीय बिंदु से परिक्रमण केंद्र की तुलना में दो गुना दूर होता है।
- (ii) यदि त्रिकोण समद्विबाहु है तो इंसेंटर उसी रेखा पर होता है।
- (iii) यदि त्रिकोण समभुज है, तो ये चारों एक ही बिंदु होते हैं।
थियोरेम्स
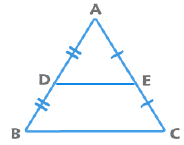
- मध्य बिंदु का प्रमेय: किसी भी दो पक्षों के मध्य बिंदु को जोड़ने वाली रेखा तीसरे पक्ष के समानांतर होती है और तीसरे पक्ष की लंबाई का आधा होती है।
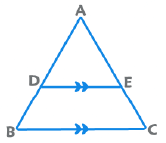
- मूल अनुपात प्रमेय: यदि DE || BC, तो AD/DB = AE/EC।
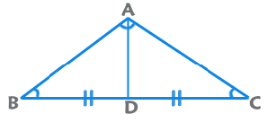
- अपोलोनियस का प्रमेय: AB² + AC² = 2 (AD² + BD²)।
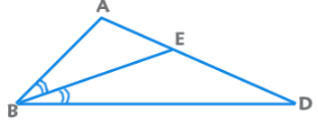
- आंतरिक कोण बिसेक्टर प्रमेय: AE/ED = BA/BD।
विशेष त्रिकोण
- समकोण त्रिकोण: ∆ABC ≈ ∆ ADB ≈ ∆ BDC; BD² = AD x DC और AB x BC = BD x DC।
- समभुज त्रिकोण: सभी कोण 60° के बराबर होते हैं। सभी पक्ष भी बराबर होते हैं। ऊँचाई = क्षेत्रफल = सम्मिलित त्रिज्या = 1/3 ऊँचाई; परिक्रमण त्रिज्या = 2/3 ऊँचाई।
- समद्विबाहु त्रिकोण: विपरीत पक्षों के बराबर कोण समान होते हैं।
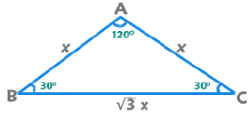
30°-60°-90° त्रिकोण क्षेत्रफल; 45°-45°-90° त्रिकोण क्षेत्रफल = x²/2; 30°-30°-120° त्रिकोण क्षेत्रफल =
त्रिकोणों की समानता
- दो त्रिकोण समान होते हैं यदि उनके संबंधित कोण समान और संबंधित पक्ष अनुपात में होते हैं।
समानता के परीक्षण: (AA / SSS / SAS)
समान त्रिकोणों के लिए, यदि पक्षों का अनुपात a:b है ⇒ संबंधित ऊँचाइयाँ a:b के अनुपात में होती हैं ⇒ संबंधित माध्यिकाएँ a:b के अनुपात में होती हैं ⇒ परिक्रमण त्रिज्याएँ a:b के अनुपात में होती हैं ⇒ सम्मिलित त्रिज्याएँ a:b के अनुपात में होती हैं ⇒ परिमाप a:b के अनुपात में होते हैं ⇒ क्षेत्रफल a² : b² के अनुपात में होते हैं।
त्रिकोणों के समकक्षता
- दो त्रिकोण समकक्ष होते हैं यदि उनके संबंधित पक्ष और कोण समकक्ष होते हैं।
समकक्षता के परीक्षण: (SSS / SAS / AAS / ASA)
समान त्रिकोणों में सभी अनुपात अब 1:1 हैं।
बहुभुज
- आंतरिक कोणों का योग = (n-2) x 180° = (2n-4) x 90°
- बाहरी कोणों का योग = 360°
- आधारों की संख्या = शीर्षों द्वारा बनाए गए त्रिकोणों की संख्या = nC3
नियमित बहुभुज:
- यदि सभी पक्ष और सभी कोण समान हैं, तो यह एक नियमित बहुभुज है। सभी नियमित बहुभुजों को एक वृत्त में अंकित या उससे परिक्रमित किया जा सकता है।
- क्षेत्रफल = ½ x परिमाप x सम्मिलित त्रिज्या {सम्मिलित त्रिज्या किसी भी पक्ष से केंद्र की लम्बवत है}
प्रत्येक आंतरिक कोण = बाहरी = 360°/n
4. चतुर्भुज
- आंतरिक कोणों का योग = बाहरी कोणों का योग = 360°
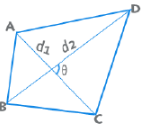
- एक चतुर्भुज का क्षेत्रफल ½ d1 d2 Sinθ द्वारा दिया जाता है।
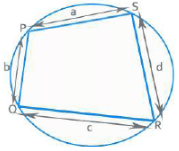
चक्रव्यूह चतुर्भुज: यदि एक चतुर्भुज के सभी शीर्ष एक वृत्त के परिधि पर होते हैं, तो इसे चक्रव्यूह चतुर्भुज कहा जाता है।
विपरीत कोण पूरक होते हैं। क्षेत्रफल = जहाँ s अर्ध परिमाप है।
EduRev की टिप: विपरीत पक्षों का योग या गुणन = विकर्णों का गुणन। यदि एक वृत्त को एक चतुर्भुज में अंकित किया जा सकता है, तो इसका क्षेत्रफल = √abcd।
चतुर्भुज के विभिन्न प्रकार
- पैरालेलोग्राम: विपरीत पक्ष समानांतर और समान होते हैं।
- विपरीत कोण समान होते हैं और लगातार कोण पूरक होते हैं।
- पैरालेलोग्राम के विकर्ण एक-दूसरे को बिसेक्ट करते हैं।
- परिमाप = 2(लगभग पक्षों का योग); क्षेत्रफल = आधार x ऊँचाई = AD x BE
EduRev की टिप: वृत्त में अंकित पैरालेलोग्राम हमेशा एक आयत होता है। वृत्त के चारों ओर अंकित पैरालेलोग्राम हमेशा एक ही रंबस होता है।
प्रत्येक विकर्ण एक पैरालेलोग्राम को दो समान क्षेत्र वाले त्रिकोणों में विभाजित करता है।
विकर्णों के वर्गों का योग = चार पक्षों के वर्गों का योग ⇒ AC² + BD² = AB² + BC² + CD² + DA²
एक आयत चार कोण बिसेक्टर के प्रतिच्छेदन से बनती है।
- रंबस: सभी पक्ष समान होते हैं। इसके विकर्ण 90° पर बिसेक्ट करते हैं।
- परिमाप = 4a; क्षेत्रफल = ½ d1 d2; क्षेत्रफल = d x
- आयत: सभी कोण समान (90°) होते हैं। इसके विकर्ण समान होते हैं। परिमाप = 2(l + b); क्षेत्रफल = lb
- वर्ग: सभी पक्ष समान और सभी कोण समान होते हैं। इसके विकर्ण समान होते हैं और 90° पर बिसेक्ट करते हैं। परिमाप = 4a; क्षेत्रफल = a²; विकर्ण = a√2
EduRev की टिप: सभी चतुर्भुजों में जिनका क्षेत्रफल दिया गया है, वर्ग का परिमाप सबसे कम होता है। सभी चतुर्भुजों में जिनका परिमाप दिया गया है, वर्ग का क्षेत्रफल सबसे अधिक होता है।
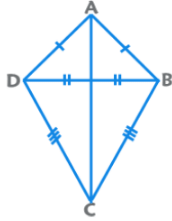
- काइट: दो जोड़े लगातार पक्ष समान होते हैं। लंबा विकर्ण छोटे विकर्ण को 90° पर बिसेक्ट करता है।
- क्षेत्रफल = विकर्णों का गुणन / 2
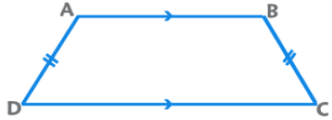
(f) ट्रेपेजियम / ट्रेपेज़ॉइड: एक चतुर्भुज जिसमें केवल एक जोड़ी पक्ष समानांतर होते हैं। समानांतर पक्षों को आधार और गैर-समानांतर पक्षों को पार्श्व पक्ष कहा जाता है।
क्षेत्रफल = ½ x (समानांतर पक्षों का योग) x ऊँचाई।
माध्यिका, पार्श्व पक्षों के मध्य बिंदुओं को जोड़ने वाली रेखा, समानांतर पक्षों के योग का आधा होती है।
EduRev की टिप: विकर्णों की लंबाई के वर्गों का योग = पार्श्व पक्षों के वर्गों का योग + 2 x आधारों का गुणन। ⇒ AC² + BD² = AD² + BC² + 2 x AB x CD
- समद्विबाहु ट्रेपेजियम: गैर-समानांतर पक्ष (पार्श्व पक्ष) समान लंबाई के होते हैं। प्रत्येक समानांतर पक्ष द्वारा पार्श्व पक्षों के साथ बनाए गए कोण समान होते हैं।
EduRev की टिप: यदि एक ट्रेपेजियम वृत्त में अंकित किया गया है, तो उसे समद्विबाहु ट्रेपेजियम होना चाहिए। यदि एक वृत्त को एक ट्रेपेजियम में अंकित किया जा सकता है, तो समानांतर पक्षों का योग = पार्श्व पक्षों का योग।
5. षट्भुज (नियमित)
- परिमाप = 6a; क्षेत्रफल =
- आंतरिक कोणों का योग = 720°।
- प्रत्येक आंतरिक कोण = 120°। बाहरी = 60°
- विकर्णों की संख्या = 9 {3 बड़े और 6 छोटे}
- बड़े विकर्णों की लंबाई (3) = 2a
- छोटे विकर्णों की लंबाई (6) = √3a
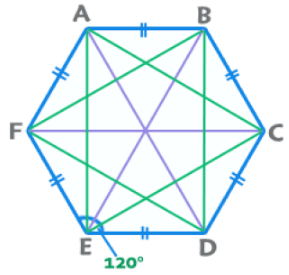
EduRev की टिप: एक नियमित षट्भुज को छह समभुज त्रिकोणों के संयोजन के रूप में माना जा सकता है। सभी नियमित बहुभुजों को 'n' समद्विभुज त्रिकोणों के संयोजन के रूप में माना जा सकता है।
पेंटागन का क्षेत्रफल = 1.72 a²; अष्टभुज का क्षेत्रफल = 2(√2 + 1) a²
6. वृत्त
- त्रिज्या = 2r; परिधि = 2πr; क्षेत्रफल = πr²
- वृत्त के केंद्र से समान दूरी पर स्थित चॉर्ड समान होते हैं।
- केंद्र से एक लम्बवत रेखा चॉर्ड को बिसेक्ट करती है।
- समान चॉर्डें केंद्र पर समान कोण बनाती हैं।
- त्रिज्या वृत्त का सबसे लंबा चॉर्ड होता है।
- एक चॉर्ड / आर्क वृत्त के परिधि पर किसी भी बिंदु पर समान कोण बनाती है और केंद्र पर उसका दो गुना बनाती है।
- समान लंबाई की चॉर्डें समान कोण बनाती हैं।
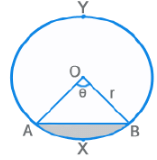
- चॉर्ड AB वृत्त को दो भागों में विभाजित करता है: माइनर आर्क AXB और मेजर आर्क AYB।
आर्क AXB का माप = ∠AOB = θ; लंबाई (आर्क AXB) = क्षेत्रफल (क्षेत्र OAXB) = माइनर सेगमेंट का क्षेत्रफल = ऊपर दी गई चित्र में छायांकित क्षेत्र ⇒ क्षेत्र OAXB का क्षेत्रफल - ∆ OAB का क्षेत्रफल।
टैंगेंट्स, सेकेंट्स और चॉर्ड्स के गुण
- त्रिज्या और टैंगेंट एक दूसरे के प्रति लम्बवत होते हैं।
- एक बाहरी बिंदु से केवल दो टैंगेंट्स हो सकते हैं, जो लंबाई में समान होते हैं। PA = PB; PA x PB = PC x PD
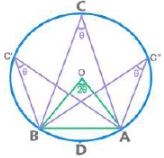
- θ = ½ [ m(Arc AC) – m(Arc BD) ]
- PA x PB = PC x PD; θ = ½ [ m(Arc AC) + m(Arc BD) ]
गुण (जारी)
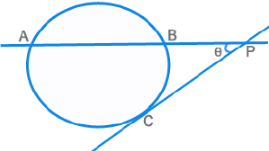
- PA x PB = PC²; θ = ½ [ m(Arc AC) - m(Arc BC) ]
वैकल्पिक खंड प्रमेय
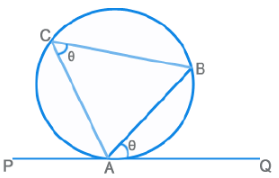
चॉर्ड AB द्वारा बनाए गए कोण का माप टैंगेंट पर A (PQ) के साथ समान होता है जो परिधि के विपरीत तरफ होता है। ⇒ ∠BAQ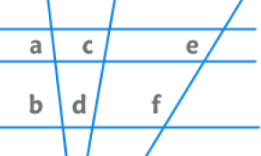
2. त्रिकोण
- एक त्रिकोण के आंतरिक कोणों का योग 180° है और बाहरी कोणों का योग 360° है।
- बाहरी कोण = दूर के आंतरिक कोणों का योग।
- दो किनारों का योग हमेशा तीसरे किनारे से अधिक होता है और दो किनारों का अंतर हमेशा तीसरे किनारे से कम होता है।
- सबसे बड़े कोण के विपरीत किनारा सबसे लंबा होता है और सबसे छोटे कोण के विपरीत किनारा सबसे छोटा होता है।
त्रिकोण का क्षेत्रफल = ½ x आधार x ऊँचाई = ½ x किनारों का गुणनफल x शामिल कोण का साइन = यहाँ s अर्ध परिधि है [s = (a + b + c)/2] = r x s [r आंतरिक वृत्त की त्रिज्या है] [R बाह्य वृत्त की त्रिज्या है]
- एक त्रिकोण का माध्यिका एक रेखा खंड है जो एक शीर्ष को विपरीत किनारे के मध्य बिंदु से जोड़ता है। तीन माध्यिकाएँ एक ही बिंदु पर मिलती हैं, जिसे त्रिकोण का केंद्रक कहा जाता है। केंद्रक माध्यिका को 2:1 के अनुपात में विभाजित करता है।
- एक त्रिकोण की ऊँचाई एक सीधी रेखा है जो एक शीर्ष से निकलती है और विपरीत किनारे या उसके विस्तार के प्रति लंबवत होती है। तीन ऊँचाइयाँ एक ही बिंदु पर मिलती हैं, जिसे त्रिकोण का ऑर्थोसेंटर कहा जाता है।
- एक लंबवत बाइसेक्टर वह रेखा है जो त्रिकोण के एक किनारे के साथ एक दाएँ कोण बनाती है और उस किनारे पर उसके मध्य बिंदु पर मिलती है। तीन लंबवत बाइसेक्टर्स एक ही बिंदु पर मिलती हैं, जिसे त्रिकोण का परिकेंद्र कहा जाता है। यह बाह्य वृत्त का केंद्र है जो त्रिकोण के सभी शीर्षों से गुजरता है।
- एक कोण बाइसेक्टर वह रेखा है जो किसी शीर्ष पर कोण को दो समान भागों में विभाजित करती है। तीन कोण बाइसेक्टर्स एक ही बिंदु पर मिलती हैं, जिसे त्रिकोण का आइन्सेंटर कहा जाता है। यह आंतरिक वृत्त का केंद्र है जो त्रिकोण के सभी किनारों को छूता है।
EduRev का सुझाव: केंद्रक और आइन्सेंटर हमेशा त्रिकोण के भीतर होते हैं।
- (i) तीव्र कोण वाले त्रिकोण के लिए, परिकेंद्र और ऑर्थोसेंटर त्रिकोण के भीतर होते हैं।
- (ii) obtuse कोण वाले त्रिकोण के लिए, परिकेंद्र और ऑर्थोसेंटर त्रिकोण के बाहर होते हैं।
- (iii) समकोण वाले त्रिकोण के लिए, परिकेंद्र लंबवत के मध्य बिंदु पर होता है और ऑर्थोसेंटर उस शीर्ष पर होता है जहाँ कोण 90° है।
ऑर्थोसेंटर, केंद्रक और परिकेंद्र हमेशा एक ही रेखा पर होते हैं जिसे यूलेर रेखा कहा जाता है।
- (i) ऑर्थोसेंटर केंद्रक से दुगने दूर होते हैं।
- (ii) यदि त्रिकोण समद्विबाहु है, तो आइन्सेंटर उसी रेखा पर होता है।
- (iii) यदि त्रिकोण समकोण है, तो सभी चार एक ही बिंदु पर होते हैं।
थिओरेम
- 1. मध्य बिंदु सिद्धांत: किसी भी दो किनारों के मध्य बिंदु को जोड़ने वाली रेखा तीसरे किनारे के समानांतर होती है और उसकी लंबाई तीसरे किनारे की आधी होती है।
- 2. बुनियादी अनुपात सिद्धांत: यदि DE || BC, तो AD/DB = AE/EC
- 3. अपोलोनियस का सिद्धांत: AB² + AC² = 2 (AD² + BD²)
- 4. आंतरिक कोण बाइसेक्टर सिद्धांत: AE/ED = BA/BD
विशेष त्रिकोण
- 1. समकोण त्रिकोण: ∆ABC ≈ ∆ ADB ≈ ∆ BDC BD² = AD x DC और AB x BC = BD x DC
- 2. समभुज त्रिकोण: सभी कोण 60° के बराबर होते हैं। सभी किनारे भी समान होते हैं। ऊँचाई = क्षेत्रफल = आंतरिक त्रिज्या = 1/3 ऊँचाई बाह्य त्रिज्या = 2/3 ऊँचाई।
- 3. समद्विबाहु त्रिकोण: समान किनारों के सामने कोण समान होते हैं।
त्रिकोणों की समानता
- यदि दो त्रिकोणों के समान कोण समान हैं और समान किनारों का अनुपात है, तो वे समान होते हैं।
- समानता के परीक्षण: (AA / SSS / SAS)
- समान त्रिकोणों के लिए, यदि किनारे a:b के अनुपात में हैं ⇒ संबंधित ऊँचाइयाँ a:b के अनुपात में हैं ⇒ संबंधित माध्यिकाएँ a:b के अनुपात में हैं ⇒ बाह्य त्रिज्या a:b के अनुपात में हैं ⇒ आंतरिक त्रिज्या a:b के अनुपात में हैं ⇒ परिधियाँ a:b के अनुपात में हैं ⇒ क्षेत्रफल a² : b² के अनुपात में हैं।
त्रिकोणों की समरूपता
- यदि दो त्रिकोणों के समान किनारे और कोण समान हैं, तो वे समरूप होते हैं।
- समरूपता के परीक्षण: (SSS / SAS / AAS / ASA)
बहुभुज
- आंतरिक कोणों का योग = (n-2) x 180° = (2n-4) x 90°
- बाहरी कोणों का योग = 360°
- आकृतियों की संख्या = उन त्रिकोणों की संख्या जो शीर्षों द्वारा बनाई जा सकती हैं = nC3
नियमित बहुभुज
- यदि सभी किनारे और सभी कोण समान हैं, तो यह एक नियमित बहुभुज है। सभी नियमित बहुभुजों को एक वृत्त में समाहित या उसके चारों ओर रखा जा सकता है।
- क्षेत्रफल = ½ x परिधि x आंतरिक त्रिज्या {आंतरिक त्रिज्या केंद्र से किसी भी किनारे तक लंबवत है}
- प्रत्येक आंतरिक कोण = बाहरी = 360°/n
चतुर्भुज
- आंतरिक कोणों का योग = बाहरी कोणों का योग = 360°
- चतुर्भुज का क्षेत्रफल ½ d1 d2 Sinθ द्वारा दिया गया है।
चक्रीय चतुर्भुज
- यदि एक चतुर्भुज के सभी शीर्ष एक वृत्त की परिधि पर स्थित हैं, तो इसे चक्रीय चतुर्भुज कहा जाता है। विपरीत कोण पूरक होते हैं।
- क्षेत्रफल = जहाँ s अर्ध परिधि है।
EduRev का सुझाव: विपरीत किनारों का योग या गुणनफल = व्यासों का गुणनफल। यदि एक वृत्त एक चतुर्भुज में समाहित किया जा सकता है, तो उसका क्षेत्रफल दिया गया है = √abcd
चतुर्भुजों के विभिन्न प्रकार
- (a) समांतर चतुर्भुज: विपरीत किनारे समानांतर और समान होते हैं। विपरीत कोण समान होते हैं और लगातार कोण पूरक होते हैं।
- समांतर चतुर्भुज के व्यास एक-दूसरे को विभाजित करते हैं।
- परिधि = 2(लगभग किनारों का योग); क्षेत्रफल = आधार x ऊँचाई = AD x BE
EduRev का सुझाव: एक वृत्त में समाहित समांतर चतुर्भुज हमेशा एक आयत होता है। एक वृत्त के चारों ओर समाहित समांतर चतुर्भुज हमेशा एक हीरे के समान होता है।
- प्रत्येक व्यास समांतर चतुर्भुज को समान क्षेत्रफल के दो त्रिकोणों में विभाजित करता है।
- व्यासों का वर्ग का योग = चार किनारों का वर्ग का योग ⇒ AC² + BD² = AB² + BC² + CD² + DA²
एक आयत समांतर चतुर्भुज के चार कोण बाइसेक्टर्स के प्रतिच्छेदन से बनती है।
- (b) हीरा: एक समांतर चतुर्भुज जिसमें सभी किनारे समान होते हैं। इसके व्यास 90° पर बिस्केट होते हैं। परिधि = 4a; क्षेत्रफल = ½ d1 d2; क्षेत्रफल = d x
- (c) आयत: एक समांतर चतुर्भुज जिसमें सभी कोण समान (90°) होते हैं। इसके व्यास समान होते हैं। परिधि = 2(l + b); क्षेत्रफल = l x b
- (d) वर्ग: एक समांतर चतुर्भुज जिसमें सभी किनारे समान और सभी कोण समान होते हैं। इसके व्यास समान होते हैं और 90° पर बिस्केट होते हैं। परिधि = 4a; क्षेत्रफल = a²; व्यास = a√2
EduRev का सुझाव: दी गई क्षेत्रफल के सभी चतुर्भुजों में, वर्ग का परिधि सबसे कम होता है। दी गई परिधि के सभी चतुर्भुजों में, वर्ग का क्षेत्रफल सबसे अधिक होता है।
- (e) पतंग: दो जोड़ी समान किनारे होते हैं। लंबा व्यास छोटा व्यास को 90° पर विभाजित करता है। क्षेत्रफल = व्यासों का गुणनफल / 2
- (f) त्रेपेज़ियम / त्रेपेज़ॉइड: एक चतुर्भुज जिसमें केवल एक जोड़ी किनारे समानांतर होते हैं, उसे त्रेपेज़ॉइड कहा जाता है। समानांतर किनारे आधार कहलाते हैं और गैर-समानांतर किनारे पार्श्व किनारे कहलाते हैं।
क्षेत्रफल = ½ x (समानांतर किनारों का योग) x ऊँचाई।
- माध्यिका, वह रेखा जो पार्श्व किनारों के मध्य बिंदुओं को जोड़ती है, समानांतर किनारों का योग का आधा होती है।
EduRev का सुझाव: व्यासों की लंबाई के वर्ग का योग = पार्श्व किनारों के वर्ग का योग + 2 x आधार का गुणनफल। ⇒ AC² + BD² = AD² + BC² + 2 x AB x CD
- समद्विबाहु त्रेपेज़ियम: गैर-समानांतर किनारे (पार्श्व किनारे) समान लंबाई के होते हैं। प्रत्येक समानांतर किनारे के साथ बनाए गए कोण समान होते हैं।
EduRev का सुझाव: यदि एक त्रेपेज़ियम को एक वृत्त में समाहित किया जा सकता है, तो उसे एक समद्विबाहु त्रेपेज़ियम होना चाहिए। यदि एक वृत्त एक त्रेपेज़ियम में समाहित किया जा सकता है, तो समानांतर किनारों का योग = पार्श्व किनारों का योग।
हैक्सागन (नियमित)
- परिधि = 6a; क्षेत्रफल =
- आंतरिक कोणों का योग = 720°।
- प्रत्येक आंतरिक कोण = 120°। बाहरी = 60°
- द्विआधारी संख्या = 9 {3 बड़े और 6 छोटे}
- बड़े व्यासों की लंबाई (3) = 2a
- छोटे व्यासों की लंबाई (6) = √3a
EduRev का सुझाव: एक नियमित हैक्सागन को छह समानभुज त्रिकोणों के संयोजन के रूप में देखा जा सकता है। सभी नियमित बहुभुजों को 'n' समद्विभुज त्रिकोणों के संयोजन के रूप में देखा जा सकता है।
पेंटागन का क्षेत्रफल = 1.72 a²
आक्टागन का क्षेत्रफल = 2(√2 + 1) a²
वृत्त
- व्यास = 2r; परिधि = 2πr; क्षेत्रफल = πr²
- एक वृत्त के केंद्र से समान दूरी पर स्थित व्यास समान होते हैं।
- केंद्र से व्यास पर लंबवत रेखा व्यास को बिस्केट करती है।
- समान व्यास समान कोणों का निर्माण करते हैं।
- व्यास वृत्त का सबसे लंबा व्यास होता है।
- एक व्यास / आर्क किसी भी बिंदु पर एक समान कोण बनाता है और केंद्र पर उसका दुगना बनाता है।
- समान लंबाई वाले व्यास समान कोण बनाते हैं।
- व्यास AB वृत्त को दो भागों में विभाजित करता है: लघु आर्क AXB और विशाल आर्क AYB।
- आर्क AXB का माप = ∠AOB = θ
- लंबाई (आर्क AXB) = क्षेत्रफल (क्षेत्र OAXB) = लघु खंड का क्षेत्रफल = ऊपर चित्र में छायांकित क्षेत्र ⇒ क्षेत्रफल क्षेत्र OAXB - क्षेत्रफल ∆OAB
स्पर्श रेखाएँ, सेकेंट और व्यासों के गुण
- त्रिज्या और स्पर्श रेखा एक-दूसरे पर लंबवत होते हैं।
- एक बाहरी बिंदु से केवल दो स्पर्श रेखाएँ हो सकती हैं, जो लंबाई में समान होती हैं। PA = PB
- PA x PB = PC x PD
- θ = ½ [ m(Arc AC) - m(Arc BD) ]
- PA x PB = PC x PD
- θ = ½ [ m(Arc AC) + m(Arc BD) ]
गुण (जारी)
- PA x PB = PC²
- θ = ½ [ m(Arc AC) - m(Arc BC) ]
वैकल्पिक खंड सिद्धांत
- चौकोर AB के साथ स्पर्श रेखा PQ द्वारा बनाए गए कोण AB के साथ 90° पर होता है।
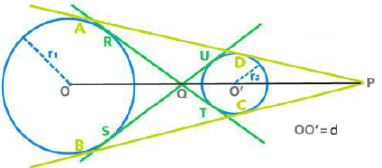
EduRev का सुझाव: दो केंद्र (O और O’), DCTs के प्रतिच्छेदन का बिंदु (P) और TCTs के प्रतिच्छेदन का बिंदु (Q) एक सीधी रेखा पर होते हैं। Q OO' को r1 : r2 के अनुपात में आंतरिक रूप से विभाजित करता है जबकि P OO' को r1 : r2 के अनुपात में बाह्य रूप से विभाजित करता है।
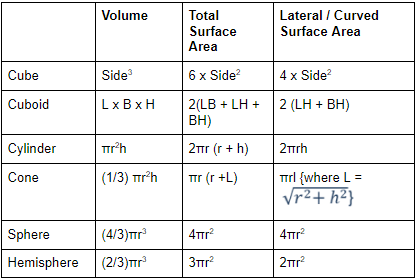
एक घन / घनाकार के चार व्यास होते हैं जिनकी लंबाई (√3 x किनारा) होती है।
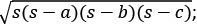
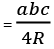
3. अपोलोनियस का प्रमेय: AB² + AC² = 2 (AD² + BD²)
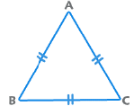
2. समबाहु त्रिकोण: सभी कोण 60° के बराबर हैं। सभी भुजाएँ भी समान हैं। ऊँचाई = क्षेत्रफल = अंतःपरिधि = 1/3 ऊँचाई, परिधि = 2/3 ऊँचाई।
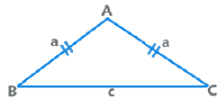
3. समद्विबाहु त्रिकोण: विपरीत भुजाओं के बराबर कोण समान होते हैं।
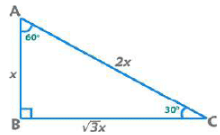
- 30°-60°-90° त्रिकोण का क्षेत्रफल
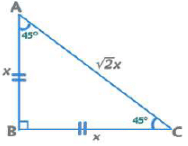
- 45°-45°-90° त्रिकोण का क्षेत्रफल = x²/2
- 30°-30°-120° त्रिकोण का क्षेत्रफल =
समानता के परीक्षण: (AA / SSS / SAS)
- आंतरिक कोणों का योग = (n-2) × 180° = (2n-4) × 90°
- बाह्य कोणों का योग = 360°
- आकृति में विकर्णों की संख्या = उस संख्या के त्रिकोण जो शीर्ष बिंदुओं द्वारा बनाये जा सकते हैं = nC3
यदि सभी भुजाएँ और सभी कोण समान हैं, तो यह एक नियमित बहुभुज है। सभी नियमित बहुभुजों को एक वृत्त में अंकित या उसके चारों ओर परिभाषित किया जा सकता है। क्षेत्रफल = ½ × परिधि × अंतःपरिधि {अंतःपरिधि किसी भी भुजा से केंद्र तक का लंबवत है} प्रत्येक आंतरिक कोण = बाह्य = 360°/n
यदि एक चतुर्भुज के सभी शीर्ष बिंदु एक वृत्त की परिधि पर स्थित हैं, तो इसे चक्रीय चतुर्भुज कहते हैं। विपरीत कोण सहपूरक होते हैं। क्षेत्रफल = जहाँ s अर्ध परिधि है।
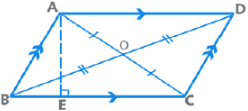
- विपरीत भुजाएँ समानांतर और समान होती हैं।
- विपरीत कोण समान होते हैं और लगातार कोण सहपूरक होते हैं।
- एक समांतर चतुर्भुज की विकर्णें एक-दूसरे को आधा करती हैं।
- परिधि = 2(सन्निकट भुजाओं का योग); क्षेत्रफल = आधार × ऊँचाई = AD × BE
EduRev का टिप:
- एक वृत्त में अंकित समांतर चतुर्भुज हमेशा एक आयत होता है।
- एक वृत्त के चारों ओर परिभाषित समांतर चतुर्भुज हमेशा एक रंबस होता है।
- प्रत्येक विकर्ण एक समांतर चतुर्भुज को दो समान क्षेत्रफल वाले त्रिकोणों में विभाजित करता है।
- विकर्णों के वर्गों का योग = चार भुजाओं के वर्गों का योग ⇒ AC² + BD² = AB² + BC² + CD² + DA²
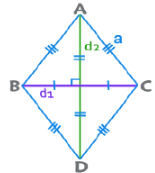
एक समांतर चतुर्भुज जिसमें सभी भुजाएँ समान होती हैं, वह रंबस होता है। इसके विकर्ण 90° पर आधा होते हैं। परिधि = 4a; क्षेत्रफल = ½ d₁ d₂; क्षेत्रफल = d ×
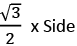
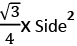
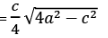
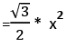
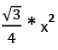
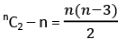
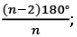
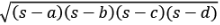
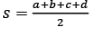
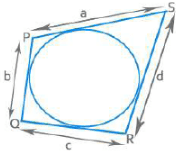
दो जोड़े सटे हुए पक्ष समान हैं। लंबा तिर्यक छोटे तिर्यक को 90° पर बिसेक्ट करता है।
- दो जोड़े सटे हुए पक्ष समान हैं।
EduRev's Tip: तिर्यकों की लंबाई के वर्गों का योग = पार्श्व पक्षों के वर्गों का योग 2 आधारों का गुणनफल। ⇒ AC² + BD² = AD² + BC² + 2 × AB × CD
गैर-समानांतर पक्ष (पार्श्व पक्ष) लंबाई में समान होते हैं। प्रत्येक समानांतर पक्ष द्वारा पार्श्व पक्षों के साथ बनाए गए कोण समान होते हैं।
EduRev's Tip: एक नियमित षट्भुज को छह समभुज त्रिकोणों के संयोजन के रूप में माना जा सकता है। सभी नियमित बहुभुजों को ‘n’ समद्विभुज त्रिकोणों के संयोजन के रूप में माना जा सकता है।
- पेंटागन का क्षेत्रफल = 1.72 a²
- ऑक्टागन का क्षेत्रफल = 2(√2 + 1) a²
व्यास = 2r; परिधि = 2πr; क्षेत्रफल = πr² केन्द्र से समान दूरी पर स्थित तंतु समान होते हैं।
- एक रेखा जो केन्द्र से तंतु के प्रति लंब है, तंतु को बिसेक्ट करती है।
- समान तंतु केन्द्र पर समान कोण बनाते हैं।
- व्यास एक वृत्त का सबसे लंबा तंतु है।
- समान लंबाई के तंतु/आर्क किसी भी बिंदु पर समान कोण बनाते हैं और केन्द्र पर उसका दो गुना।
- तंतु/आर्क की समान लंबाई समान कोण बनाती है।
- तंतु AB वृत्त को दो भागों में विभाजित करता है: छोटी आर्क AXB और बड़ी आर्क AYB.
- आर्क AXB का माप = ∠AOB = θ
- लंबाई (आर्क AXB) = क्षेत्रफल (क्षेत्र OAXB) = छोटी खंड का क्षेत्रफल = ऊपर चित्र में छायांकित क्षेत्र ⇒ क्षेत्रफल OAXB का क्षेत्रफल - ∆ OAB का क्षेत्रफल
छोटी खंड का क्षेत्रफल = ऊपर चित्र में छायांकित क्षेत्र ⇒ क्षेत्रफल क्षेत्र OAXB - ∆ OAB का क्षेत्रफल
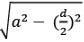
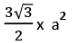
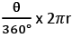
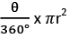
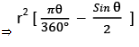
- त्रिज्या और स्पर्शरेखा एक-दूसरे के प्रति लंबवत होती हैं।
- एक बाहरी बिंदु से केवल दो स्पर्शरेखाएँ खींची जा सकती हैं, जो लंबाई में समान होती हैं: PA = PB
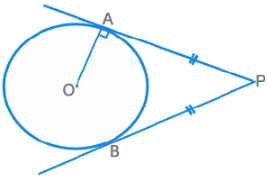
- PA x PB = PC x PD
- θ = ½ [ m(Arc AC) – m(Arc BD) ]
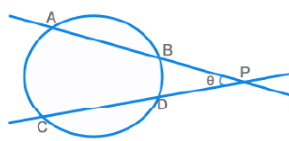
- PA x PB = PC x PD
- θ = ½ [ m(Arc AC) + m(Arc BD) ]
गुणधर्म (जारी)
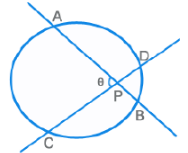
PA x PB = PC²
θ = ½ [ m(Arc AC) - m(Arc BC) ]
कोण जो AB chord द्वारा A पर स्पर्शरेखा (PQ) के साथ बनता है, वह परिधि के विपरीत किनारे पर बनते कोण के समान होता है। ⇒ ∠BAQ = ∠ACB
⇒ AD = BC = लंबवत सामान्य स्पर्शरेखा (TCT) की लंबाई ⇒ RT = SU =
EduRev का सुझाव:
- दो केंद्र (O और O’), DCTs का इंटरसेक्शन बिंदु (P) और TCTs का इंटरसेक्शन बिंदु (Q) एक सीधी रेखा में होते हैं।
- Q, OO’ को r1 : r2 के अनुपात में आंतरिक रूप से विभाजित करता है जबकि P, OO’ को r1 : r2 के अनुपात में बाहरी रूप से विभाजित करता है।
- एक घन / घनाकार में 4 बॉडी विकर्ण होते हैं जिनकी लंबाई (√3 x side) होती है।
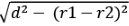
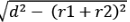
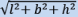
|
142 videos|172 docs|185 tests
|















