बुनियादी त्रिकोणमिति के सिद्धांत | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download

त्रिकोणमिति क्या है?

त्रिकोणमिति गणित की वह शाखा है जो त्रिकोण के भुजाओं और कोणों के बीच के संबंधों का अध्ययन करती है। यह ग्रीक शब्द 'Trigonon' और 'metron' से निकला है, जहाँ Tri का अर्थ है तीन, Gon का अर्थ है कोण और Metron का अर्थ है माप।

• एक समकोण त्रिकोण के दो भुजाओं की लंबाइयों का अनुपात को त्रिकोणमितीय अनुपात कहा जाता है।
• त्रिकोण के त्रिकोणमितीय अनुपातों को त्रिकोणमितीय कार्य भी कहा जाता है।
• कुल मिलाकर छह त्रिकोणमितीय अनुपात हैं।
• Sine (साइन), cosine (कोसाइन), और tangent (टैन्जेंट) तीन महत्वपूर्ण त्रिकोणमितीय कार्य हैं और इन्हें क्रमशः sin, cos, और tan के संक्षेप में लिखा जाता है।

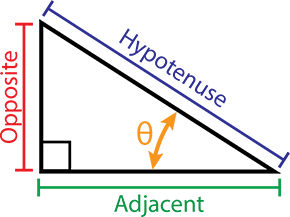
एक समकोण त्रिकोण ABC पर विचार करें, जहाँ सबसे लंबी भुजा को हाइपोटेन्यूज कहा जाता है, और हाइपोटेन्यूज के विपरीत भुजाओं को सन्निकट और विपरीत भुजाएँ कहा जाता है।

• AC = त्रिकोण का हाइपोटेन्यूज
• AB = कोण ABC के लिए सन्निकट भुजा
• BC = कोण A के लिए विपरीत भुजा

समकोण त्रिकोण ABC के त्रिकोणमितीय अनुपात जब ∠B = 90° हो:

• (i) sin A = कोण A का साइन = (कोण A के विपरीत भुजा / हाइपोटेन्यूज) = (BC/AC)
• (ii) cos A = कोण A का कोसाइन = (कोण A के लिए सन्निकट भुजा / हाइपोटेन्यूज) = (AB/AC)
• (iii) tan A = कोण A का टैन्जेंट = (कोण A के विपरीत भुजा / कोण A के लिए सन्निकट भुजा) = (BC/AB)
• (iv) cosec A = कोण A का कोसेकेंट = हाइपोटेन्यूज / कोण A के लिए विपरीत भुजा = 1/sin A
• (v) sec A = कोण A का सेकेंट = हाइपोटेन्यूज / सन्निकट भुजा = 1/cos A
• (vi) cot A = कोण A का कोटैन्जेंट = सन्निकट भुजा / विपरीत भुजा = 1/tan A

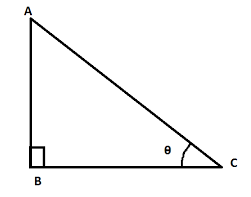
समकोण त्रिकोण ABC के त्रिकोणमितीय अनुपात जहाँ ∠B = 90°

• sin A = ∠A का साइन = (∠A के विपरीत भुजा / कर्ण) = (BC/AC)
• cos A = ∠A का कोसाइन = (∠A के निकटवर्ती भुजा / कर्ण) = (AB/AC)
• tan A = ∠A का टैंजेंट = (∠A के विपरीत भुजा / ∠A के निकटवर्ती भुजा) = (BC/AB)
• cosec A = ∠A का कोसेकेंट = कर्ण / ∠A के विपरीत भुजा = 1/sin A
• sec A = ∠A का सेकेंट = कर्ण / निकटवर्ती भुजा = 1/cos A
• cot A = ∠A का कोटैंजेंट = निकटवर्ती भुजा / विपरीत भुजा = 1/tan A

त्रिकोणमिति के समस्याओं में सामान्यतः उपयोग किए जाने वाले कोण 0°, 30°, 45°, 60° और 90° हैं। इन कोणों के त्रिकोणमितीय अनुपात जैसे साइन, कोसाइन और टैंजेंट को याद करना आसान है। उदाहरण: एक समकोण त्रिकोण में:

• ⇒ Sin θ = लंबवत / कर्ण या θ = sin^-1 (P/H)
• ⇒ इसी प्रकार, θ = cos^-1 (आधार / कर्ण)
• θ = tan^-1 (लंबवत / आधार)

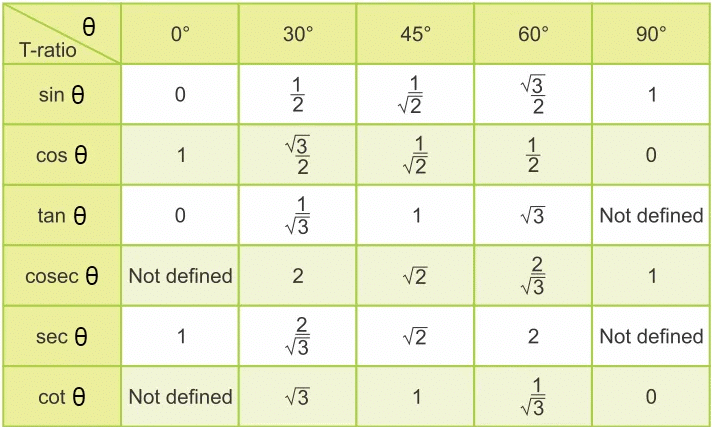
विशेष कोणों के त्रिकोणमितीय अनुपात

• विशेष कोणों के त्रिकोणमितीय अनुपात, अर्थात् 0°, 30°, 45°, 60°, 90°, एक पैटर्न का पालन करते हैं और उन्हें याद करना आसान है।
• इन पैटर्नों की पहचान करना और उन्हें याद रखना इन कोणों से संबंधित समस्याओं को हल करने में मदद करता है।

• दो कोणों को इस स्थिति में पूरक कहा जाता है यदि उनका योग 90° हो। इस प्रकार ϴ और (90 – ϴ) पूरक कोण हैं।
• इन मानक कोणों के संदर्भ में पूरक कोणों का प्रतिनिधित्व करना त्रिकोणमितीय अनुपातों से संबंधित जटिल समस्याओं को हल करने में मदद करता है।

पूरक कोणों के त्रिकोणमितीय अनुपात

sin(90° – A) = cos A
cos(90° – A) = sin A
tan(90° – A) = cot A
cot(90° – A) = tan A
sec(90° – A) = cosec A
cosec(90° – A) = sec A

मूलभूत त्रिकोणमितीय पहचानें

• sin²θ + cos²θ = 1
• tan²θ + 1 = sec²θ
• cot²θ + 1 = cosec²θ
• cosθ / sinθ = cotθ

योग और अंतर की पहचानें

कोणों u और v के लिए, हमारे पास निम्नलिखित संबंध हैं:

• sin(u + v) = sin(u)cos(v) + cos(u)sin(v)
• cos(u + v) = cos(u)cos(v) – sin(u)sin(v)
• tan(u + v) = (tan(u) + tan(v)) / (1−tan(u)tan(v))
• sin(u – v) = sin(u)cos(v) – cos(u)sin(v)
• cos(u – v) = cos(u)cos(v) + sin(u)sin(v)
• tan(u – v) = (tan(u) − tan(v)) / (1 + tan(u)tan(v))

कोण में π/2 या π या नकारात्मक चिह्न के परिवर्तन से मान परिवर्तन

जब θ का कोण π/2 या π से बदला जाता है, तो त्रिकोणमितीय कार्यों के मान सरल तरीकों से बदलते हैं।

1. π/2 द्वारा परिवर्तन:

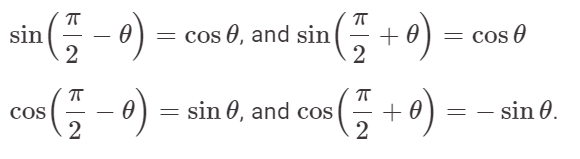
2. π द्वारा परिवर्तन:

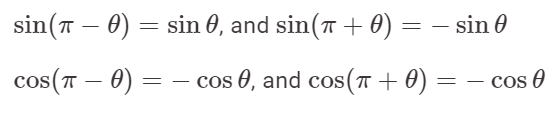
3. चिह्न द्वारा परिवर्तन:

sin(−θ) = −sinθ, और cos(−θ) = cosθ।

दो विशेष त्रिकोण

• हमें दो विशेष त्रिकोणों के बारे में जानने की आवश्यकता है: 45°-45°-90° और 30°-60°-90° त्रिकोण। ये नीचे चित्रित हैं।

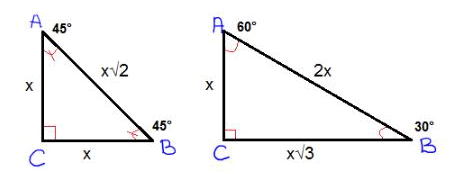
• चित्र यह दिखाते हैं कि इन विशेष त्रिकोणों की भुजाओं की लंबाई कैसे ज्ञात की जाए।
• 45-45-90 त्रिकोण ABC में, भुजाओं का अनुपात AC:BC:AB = 1:1:1/√2 है।
• 60-30-90 त्रिकोण ABC में, भुजाओं का अनुपात AC:BC:AB = 1:1/√3:2 है।

त्रिकोणमिति का अनुप्रयोग - ऊँचाई और दूरी

इस समस्या क्षेत्र में, एक वस्तु सतह पर खड़ी होती है और दूर से उस वस्तु का अवलोकन किया जाता है। यदि ऊँचाई या वस्तु की दूरी में से एक ज्ञात है, तो दूसरे को ज्ञात किया जा सकता है।

1. ऊँचाई का कोण (Angle of Elevation)

जब अवलोकक एक ऊँची वस्तु के शीर्ष की ओर देखता है, तो अवलोकन के बिंदु के माध्यम से क्षैतिज रेखा और वस्तु के शीर्ष से अवलोकन के बिंदु तक की रेखा के बीच बना कोण ऊँचाई का कोण कहलाता है।

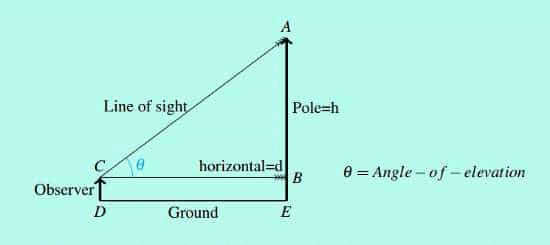
हमारे पास यहाँ, h/d = tanθ है।

2. अवसरण का कोण (Angle of Depression)

जब एक अवलोकक एक ऊँची वस्तु के शीर्ष से नीचे देखता है, तो हमें अवसरण का कोण प्राप्त होता है।

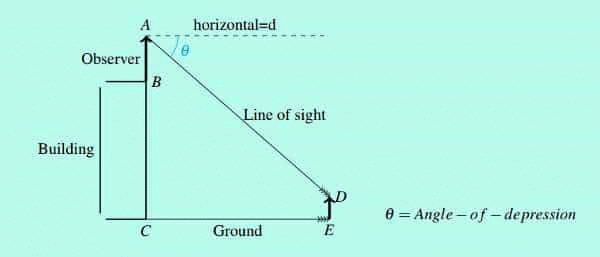
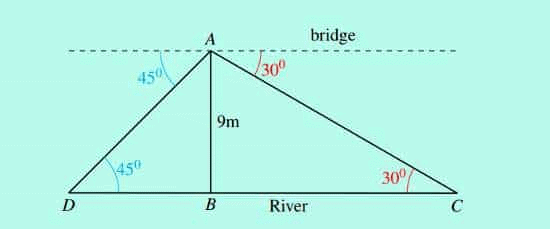
उदाहरण: नदी पर एक पुल के बिंदु A से, नदी के विपरीत किनारों के अवसरण के कोण क्रमशः 30º और 45º हैं। यदि पुल नदी की सतह से 9 मीटर की ऊँचाई पर है, तो पता करें कि नदी की चौड़ाई कितनी है।

नदी की चौड़ाई DC है। त्रिकोण △ABC में, tan 30º = AB/BC है।

समाधान:

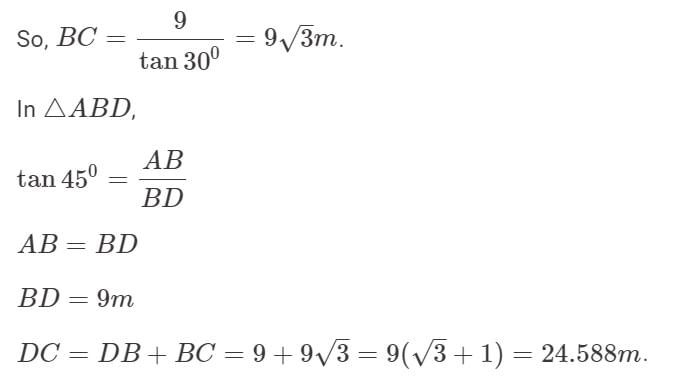
महत्वपूर्ण हल किए गए उदाहरण

आइए कुछ उदाहरणों पर ध्यान दें ताकि हम इस अवधारणा को बेहतर ढंग से समझ सकें:

उदाहरण 1: अनिल ने अपने नाव से एक लाइटहाउस के शीर्ष की ओर देखा और पाया कि ऊँचाई का कोण 30º है। लाइटहाउस की ओर 50 मीटर सीधी रेखा में जाने के बाद, उसने पाया कि ऊँचाई का कोण 45º में बदल गया। लाइटहाउस की ऊँचाई ज्ञात करें। a. 25 b. 25√3 c. 25(√3-1) d. 25(√3 + 1) उत्तर: विकल्प (d) सही है।

समाधान:

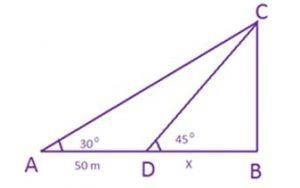
यदि हम ऊपर की छवि को देखें, तो A नाव का पूर्ववर्ती स्थान है। इस बिंदु से लाइटहाउस के शीर्ष की ओर ऊँचाई का कोण 30 डिग्री है। 50 मीटर की यात्रा करने के बाद, अनिल बिंदु D पर पहुँचता है जहाँ ऊँचाई का कोण 45 डिग्री है। C लाइटहाउस का शीर्ष है।

मान लीजिए BD = x ⇨ अब, हम जानते हैं कि tan 30 डिग्री = 1/√3 = BC/A ⇨ Tan 45 डिग्री = 1 ⇨ BC = BD = x इस प्रकार, 1/√3 = BC/AB = BC/(AD + DB) = x/(50 + x) इस प्रकार, x (√3 -1) = 50 या x= 25(√3 + 1) मीटर।

उदाहरण 2: एक विमान जब 3125 मीटर की ऊँचाई पर उड़ रहा होता है, तो वह उसी क्षण में दूसरे विमान के ठीक नीचे से गुजरता है जब जमीन पर एक ही बिंदु से दोनों विमानों के ऊँचाई के कोण क्रमशः 30º और 60º होते हैं। उस क्षण में दोनों विमानों के बीच की दूरी ज्ञात करें।

मान लीजिए C और D दो विमान हैं, और A अवलोकन का बिंदु है। तब, इस प्रकार, दोनों विमानों के बीच की दूरी 6250 मीटर है।

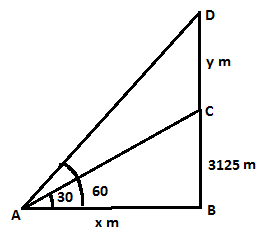
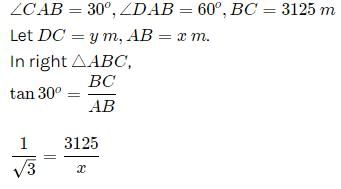
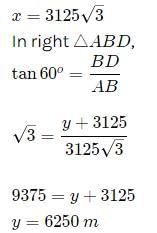
उदाहरण 3: एक विमान जो जमीन से 3000 मीटर की ऊँचाई पर उड़ रहा है, उसी क्षण में एक अन्य विमान के ठीक ऊपर से गुजरता है जब जमीन पर एक ही बिंदु से दोनों विमानों के ऊँचाई के कोण क्रमशः 60º और 45º होते हैं। जमीन से नीचे विमान की ऊँचाई है:

• a. 1000√3 मीटर
• b. 1000/√3 मीटर
• c. 500 मीटर
• d. 1500(√3 + 1)

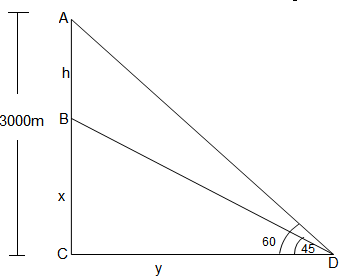
मान लीजिए कि ऊँचाई वाला विमान इस प्रकार उड़ रहा है कि बिंदु A से बिंदु D का ऊँचाई का कोण 60º है। मान लीजिए कि निम्न स्तर पर उड़ने वाले विमान की ऊँचाई CD = y है (चूंकि tan 45º = 1) ⇨ tan 60º = 3000/y ⇨ √3 = 3000/y ⇨ y = 3000/√3 = 1000√3

उदाहरण 4: यदि tan A = ¾ हो तो (1-CosA) / (1 + CosA) का मान क्या है?

• a. 1/4
• b. 9/16
• c. 1/9
• d. 1/3

हल: हम जानते हैं कि tan A = विपरीत पक्ष / समीप पक्ष = 3/4

इसलिए, विपरीत पक्ष = 3, समीप पक्ष = 4 और कर्ण = 5

इसलिए, cos A = 4/5 इस प्रकार, (1-Cos A) / (1 + Cos A) = (1 - (4/5)) / (1 - (4/5)) = 1/9

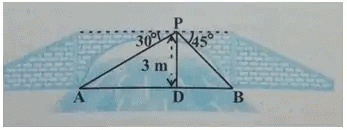
उदाहरण 5: एक पुल से जो नदी पर है, नदी के विपरीत किनारों के अवसाद के कोण क्रमशः 30 डिग्री और 45 डिग्री हैं। यदि पुल किनारों से 3 मीटर की ऊंचाई पर है, तो नदी की चौड़ाई ज्ञात कीजिए।

हल: नीचे दिए गए चित्र में, A और B नदी के विपरीत किनारों पर बिंदु दर्शाते हैं। P पुल पर 3 मीटर की ऊंचाई पर एक बिंदु है। AB की लंबाई नदी की चौड़ाई है।

अब, AB = AD + DB

सही Δ APD में, कोण A = 30°

इसलिए, tan 30° = PD / AD

या 1/√3 = 3 / AD या AD = 3√3 मीटर

इसके अलावा, सही Δ PBD में, कोण B = 45°। इसलिए, BD = PD = 3 मीटर

अब, AB = BD + AD = 3 + 3√3 मीटर

उदाहरण 6: 3sinx + 4cosx ≥ r हमेशा 0 से बड़ा या उसके बराबर है। 'r' का सबसे छोटा मान क्या हो सकता है? क. 5 ख. -5 ग. 4 घ. 3 उत्तर: विकल्प (क) सही है।

हल: 3sinx + 4cosx ≥ -r 5(3/5sinx + 4/5cosx) ≥ -r 3/5 = cosA => sinA = 4/5

5(sinx cosA + sinA cosx) ≥ -r 5(sin(x + A)) ≥ -r 5sin(x + A) ≥ -r -1 ≤ sin(angle) ≤ 1 5sin(x + A) ≥ -5

rmin = 5

उदाहरण 7: Sin(2014x) Cos(2014x) = 1, x की सीमा [-5π, 5π] में, x कितने मान ले सकता है? क. 0 ख. 10 ग. 21 घ. 11 उत्तर: विकल्प (ग) सही है।

हल: हम जानते हैं कि Sin(2x) Cos(2x) = 1 सभी x के मानों के लिए। यदि Sin x या Cos x –1 या 1 के बराबर है, तो Sin(2014x) Cos(2014x) 1 के बराबर होगा। Sin x –1 या 1 के बराबर होता है जब x = –4.5π, –3.5π, –2.5π, –1.5π, –0.5π, 0.5π, 1.5π, 2.5π, 3.5π, या 4.5π। Cos x –1 या 1 के बराबर होता है जब x = –5π, –4π, –3π, –2π, –π, 0, π, 2π, 3π, 4π, या 5π। अन्य सभी मानों के लिए, Sin(2014x) हमेशा Sin(2x) से कम होगा। अन्य सभी मानों के लिए, Cos(2014x) हमेशा Cos(2x) से कम होगा। हम जानते हैं कि Sin(2x) Cos(2x) 1 के बराबर है। इसलिए, Sin(2014x) Cos(2014x) अन्य सभी मानों के लिए 1 के बराबर नहीं होगा। इस प्रकार कुल 21 मान हैं।

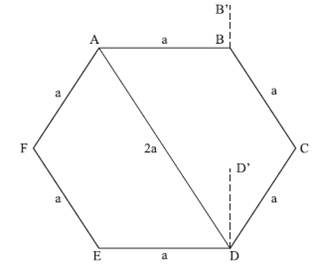
उदाहरण 8: मान लीजिए कि एक नियमित षट्भुज ABCDEF है। B और D पर टावर लगाए गए हैं। A से B पर टावर के लिए ऊंचाई का कोण 30 डिग्री है, और D पर टावर के शीर्ष के लिए 45 डिग्री है। B और D पर टावरों की ऊंचाइयों का अनुपात क्या है? a. 1:√3 b. 1:2√3 c. 1:2 d. 3:4√3 उत्तर: विकल्प (b) सही है।

समाधान: जब आप दर्पण के माध्यम से अपने प्रतिबिंब को देखते हैं, तो छवि उस दूरी पर होती है जो दर्पण और आप के बीच होती है। अब, सोचिए कि इसका त्रिकोणमिति से क्या संबंध है।

मान लीजिए कि षट्भुज ABCDEF की भुजा 'a' है। रेखा AD = 2a है। मान लीजिए कि B और D पर टावर B'B और D'D हैं। दिए गए डेटा के अनुसार, हमें पता है कि ∠B´AB = 30° और ∠D´AB = 45°। ध्यान रखें कि टावर B'B और D'D उसी तल पर नहीं हैं जैसे षट्भुज। त्रिकोण B'AB में, Tan∠B´AB = B´AB = B′B/AB = 1/3 => B’B = a/√3। त्रिकोण D´AD में, tan ∠D´AD = D′D/AD = 1 => D’D = 2a। ऊंचाइयों का अनुपात = 1/√3 या 1/2√3 उत्तर विकल्प (B)

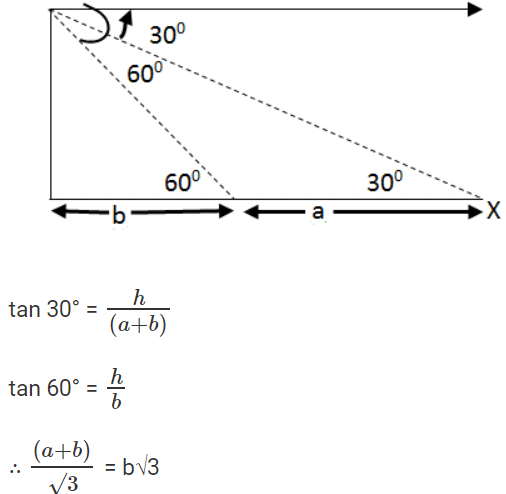
उदाहरण 9: एक व्यक्ति एक टावर के शीर्ष पर खड़ा है और एक कार को टावर की ओर आते हुए देखता है। यदि 30° से 60° तक के अवनति के कोण को बदलने में 20 मिनट लगते हैं, तो कार के टावर तक पहुँचने के लिए शेष समय क्या है? a. 20√3 मिनट b. 20 मिनट c. 10 मिनट d. 20√3 मिनट

उत्तर: विकल्प (c) सही है। समाधान: => a b = 3b => 2b = a => b = a²/a²। अब चूंकि कार को एक दूरी तय करने में 20 मिनट लगते हैं। b की दूरी तय करने में समय = a/2 = 20² = 10 मिनट

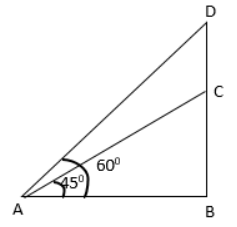
उदाहरण 10: एक छात्र 100 मीटर ऊँची कॉलेज बिल्डिंग के शीर्ष पर एक बैनर के साथ खड़ा है। जमीन पर एक बिंदु से, छात्र के शीर्ष का ऊंचाई का कोण 60° है और उसी बिंदु से, टावर के शीर्ष का ऊंचाई का कोण 45° है। छात्र की ऊँचाई ज्ञात कीजिए। a. 35 मीटर b. 73.2 मीटर c. 50 मीटर d. 75 मीटर उत्तर: विकल्प (b) सही है।

समाधान: BC को टॉवर की ऊँचाई और DC को छात्र की ऊँचाई मान लें। rt. ∆ ABC में AB = BC cot 45° AB = 100 मीटर

• (i) rt. ∆ ABD में AB = BD cot 60° AB = (BC CD) cot 60° AB = (10 CD)*1/√3

• (ii) (i) और (ii) को समान करते हुए: (10 CD) * 1/√3 = 100

• (10 CD) = 100√3

• CD = 100√3 – 100 = 10(1.732 – 1) = 100 * 0.732 = 73.2 मीटर

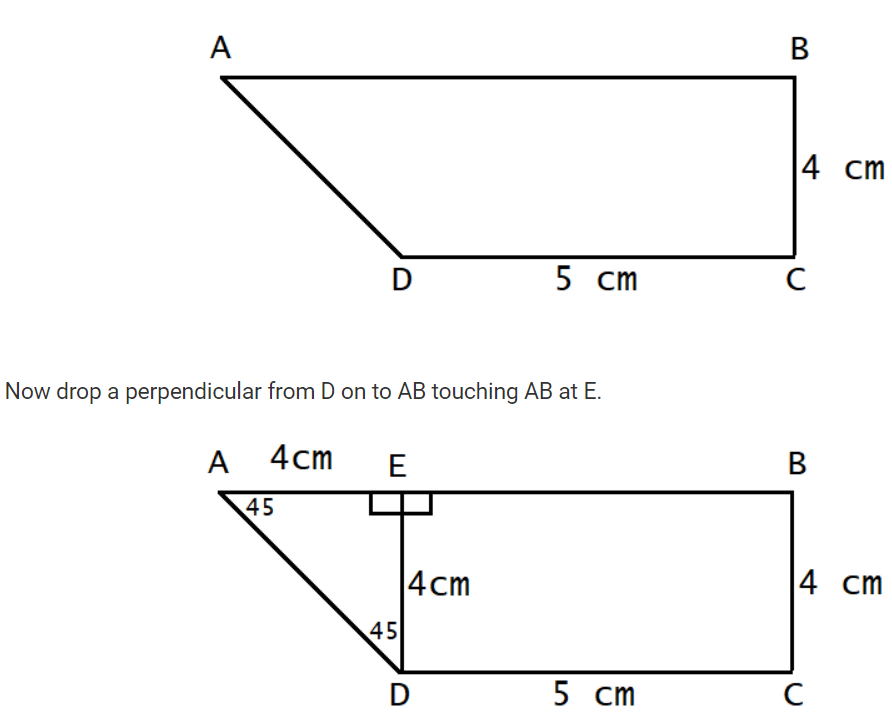
उदाहरण 11: एक समतल ABCD में, AB DC के समानांतर है, BC DC के लंबवत है और ∠BAD = 45° है। यदि DC = 5 सेमी, BC = 4 सेमी है, तो समतल का क्षेत्रफल वर्ग सेमी में है:

• a. 22 cm²
• b. 29 cm²
• c. 28 cm²
• d. 32 cm²

उत्तर: विकल्प (c) सही है।

समाधान: चलिए एक समतल पर विचार करते हैं। ΔAED में, ∠AED = 90°, ∠DAE = 45°, इसलिए ∠EDA = 45°। स्पष्ट है कि ΔAED एक समकोण समद्विबाहु त्रिकोण है और चतुर्भुज BCDE एक आयत है। इसलिए, BC = DE = 4 सेमी। चूंकि ΔAED एक समद्विबाहु त्रिकोण है, AE = ED = 4 सेमी।

समतल का क्षेत्रफल = ΔAED का क्षेत्रफल + आयत BCDE का क्षेत्रफल

समतल का क्षेत्रफल = (1/2) × AE × ED × DC × BC

समतल का क्षेत्रफल = (1/2) × 4 × 4 × 5 × 4

समतल का क्षेत्रफल = 8 × 20

समतल का क्षेत्रफल = 28 cm²