सूत्र: त्रिकोणमिति सूत्र और पहचानें | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download

त्रिकोणमिति सूत्र

त्रिकोणमिति त्रिकोणों के कोणों और भुजाओं के बीच संबंधों का अध्ययन करती है, जिसमें "त्रिकोण" त्रिकोण को संदर्भित करता है और "मिति" माप को। त्रिकोणमिति सूत्र जटिल समस्याओं को हल करने के लिए एक साधन प्रदान करते हैं, जो कोणों, दूरियों, और विभिन्न ज्यामितीय अवधारणाओं से संबंधित होते हैं। यह संग्रह सभी त्रिकोणमिति सूत्रों को शामिल करता है, साथ ही कार्य मानों वाली एक तालिका भी।

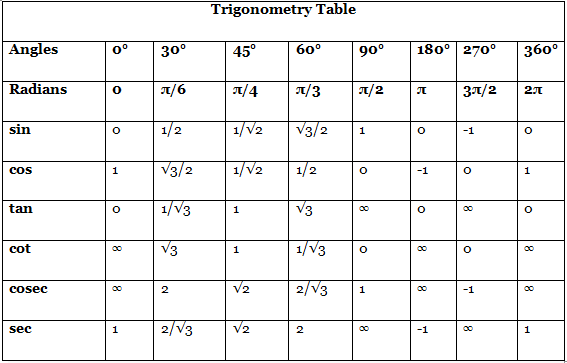
त्रिकोणमिति तालिका

त्रिकोणमिति की गणितीय सूत्रों में जाने से पहले, त्रिकोणमिति तालिका का अर्थ समझना आवश्यक है। "त्रिकोणमिति" शब्द दो भागों से मिलकर बना है: "त्रिकोण," जो त्रिकोण को दर्शाता है, और "मिति," जो माप को दर्शाता है। इस प्रकार, त्रिकोणमिति मूल रूप से त्रिकोणों के माप और समझ से संबंधित है। नीचे एक चार्ट प्रस्तुत किया गया है, जिसमें त्रिकोणमिति में सामान्यतः उपयोग किए जाने वाले कोण सूत्र दिए गए हैं, ताकि समस्याओं को हल करने में सुविधा हो।

त्रिकोणमितीय अनुपात

त्रिकोणमिति अनुपात त्रिकोणों के भीतर कोणों और भुजाओं के बीच संबंध स्थापित करते हैं। sine (sin) को विपरीत भुजा और अनुप्रस्थ भुजा के अनुपात के रूप में परिभाषित किया जाता है, cosine (cos) को सन्निकट भुजा और अनुप्रस्थ भुजा के अनुपात के रूप में, और tangent (tan) को विपरीत भुजा और सन्निकट भुजा के अनुपात के रूप में। ये अनुपात त्रिकोण से संबंधित समस्याओं को हल करने और भौतिकी और अभियांत्रिकी जैसे विभिन्न क्षेत्रों में तरंग घटनाओं का मॉडल बनाने में सहायक होते हैं। आइए सही त्रिकोणों के लिए त्रिकोणमितीय अनुपात में गहराई से जाएं।

बुनियादी त्रिकोणमिति कार्यों का सूत्र

6 बुनियादी त्रिकोणमितीय कार्य हैं: sine (sin), cosine (cos), tangent (tan), cosecant (csc), secant (sec), और cotangent (cot)। यहाँ त्रिकोणमितीय कार्य, पहचान, और कुछ मूल सूत्र दिए गए हैं:

• sine (sin) = विपरीत भुजा / अनुप्रस्थ भुजा
• cosine (cos) = सन्निकट भुजा / अनुप्रस्थ भुजा
• tangent (tan) = विपरीत भुजा / सन्निकट भुजा
• cosecant (csc) = 1 / sin
• secant (sec) = 1 / cos
• cotangent (cot) = 1 / tan

ट्रिगोनोमेट्रिक अनुपात

• sin θ = विपरीत भुजा/हाइपोटेन्यूज
• cos θ = समवर्ती भुजा/हाइपोटेन्यूज
• tan θ = विपरीत भुजा/समवर्ती भुजा
• sec θ = हाइपोटेन्यूज/समवर्ती भुजा
• cosec θ = हाइपोटेन्यूज/विपरीत भुजा
• cot θ = समवर्ती भुजा/विपरीत भुजा

यूनिट सर्कल के लिए ट्रिगोनोमेट्रिक अनुपात

यूनिट सर्कल के ट्रिगोनोमेट्रिक अनुपात कोणों और निर्देशांकों के चारों ओर घूमते हैं, जहाँ साइन (sin) y-निर्देशांक का प्रतिनिधित्व करता है, कोसाइन (cos) x-निर्देशांक से संबंधित होता है, और टैन्जेंट (tan) sin और cos का अनुपात होता है। ये अनुपात वृत्तीय गति, आवधिक कार्यों और जटिल संख्याओं पर मूल्यवान दृष्टिकोण प्रदान करते हैं, जो गणित, भौतिकी और इंजीनियरिंग जैसे विषयों में महत्वपूर्ण भूमिका निभाते हैं।

सामान्यतः, यूनिट सर्कल के लिए, त्रिज्या 1 के बराबर होती है, और θ कोण होता है। यहाँ हाइपोटेन्यूज और समवर्ती भुजा का मान यूनिट सर्कल की त्रिज्या के बराबर होता है।

हाइपोटेन्यूज = समवर्ती भुजा के लिए θ = 1

इसलिए, ट्रिगोनोमेट्री के अनुपात निम्नलिखित दिए गए हैं:

• sin θ = y/1 = y
• cos θ = x/1 = x
• tan θ = y/x
• cot θ = x/y
• sec θ = 1/x
• cosec θ = 1/y

ट्रिगोनोमेट्री पहचान

ट्रिगोनोमेट्रिक पहचानें आवश्यक समीकरण बनाती हैं जो विभिन्न ट्रिगोनोमेट्रिक कार्यों के बीच संबंध को परिभाषित करती हैं। ये समीकरण सभी कोणों के लिए मान्य रहते हैं और ट्रिगोनोमेट्रिक कार्यों को शामिल करने वाले समीकरणों को सरल बनाने और हल करने में मदद करते हैं। ट्रिगोनोमेट्री विशेष तकनीकों का उपयोग करती है जिन्हें "पहचान" कहा जाता है, जटिल ट्रिगोनोमेट्रिक प्रश्नों को तेजी और आसानी से हल करने के लिए उपयोगी उपकरण प्रदान करती हैं। आइए कुछ प्रमुख पहचानों पर एक साथ चर्चा करें।

परस्पर और भाग पहचान

परस्पर और भाग पहचान त्रिकोणमितीय कार्यों के बीच संबंध प्रदान करती हैं, जिन पर नीचे चर्चा की गई है।

परस्पर पहचान

कोसेकेंट (cosec) 1/sin है, सेकेन्ट (sec) 1/cos है, और कोटेंजेंट (cot) 1/tan है। ये संबंध त्रिकोणमितीय कार्यों और उनके परस्पर संबंधों को जोड़ते हैं, जिससे अभिव्यक्तियों को सरल करना और त्रिकोणमिति में समीकरणों को हल करना आसान होता है।

• sin θ = 1/cosec θ
• cos θ = 1/sec θ
• tan θ = 1/cot θ
• cosec θ = 1/sin θ
• sec θ = 1/cos θ
• cot θ = 1/tan θ

टैंगेंट पहचान tan θ = sin θ / cos θ और कोटैंगेंट पहचान cot θ = 1 / tan θ (cos θ / sin θ) के बीच संबंध प्रदान करती हैं।

त्रिकोणमितीय कार्यों की श्रेणियाँ

त्रिकोणमिति कार्यों जैसे साइन (sine), कोसाइन (cosine), टैंगेंट (tangent), कोटैंगेंट (cotangent), सेकेन्ट (secant) और कोसेकेंट (cosecant) की श्रेणियाँ निम्नलिखित हैं:

• −1 ≤ sin θ ≤ 1
• −1 ≤ cos θ ≤ 1
• −∞ ≤ tan θ ≤ ∞
• csc θ ≥ 1 और csc θ ≤ −1
• sec θ ≥ 1 और sec θ ≤ −1
• −∞ ≤ cot θ ≤ ∞

पाइथागोरियन पहचान

पाइथागोरियन प्रमेय त्रिकोणमिति में पाइथागोरियन पहचान का आधार है, जो एक समकोण त्रिकोण में कोण के त्रिकोणमितीय कार्यों के बीच संबंध स्थापित करती है। पाइथागोरियन प्रमेय स्वयं यह утвержित करती है कि एक समकोण त्रिकोण में, कर्ण की लंबाई का वर्ग अन्य दो भुजाओं की लंबाई के वर्गों के योग के बराबर होता है। पाइथागोरियन पहचान विशेष रूप से त्रिकोणमिति में एक कोण के साइन और कोसाइन कार्यों को संबंधित करती है।

पाइथागोरियन पहचान यह बताती है कि sin²θ + cos²θ = 1 और csc²θ – cot²θ = 1, जो समकोण त्रिकोण में त्रिकोणमितीय कार्यों को जोड़ती है। ये मौलिक समीकरण त्रिकोणमिति में साइन, कोसाइन, सेकेन्ट, कोसेकेंट, और कोटैंगेंट के बीच संबंध स्थापित करने के लिए व्यापक रूप से उपयोग किए जाते हैं।

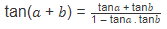
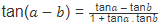
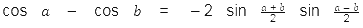
विपरीत त्रिकोणमिति सूत्र और कार्य

विपरीत त्रिकोणमिति सूत्र गणित में विशेष नियमों के रूप में कार्य करते हैं, जो विपरीत त्रिकोणमितीय कार्यों के उपयोग के माध्यम से कोणों और मानों का निर्धारण करने में सहायक होते हैं। इन्हें विपरीत त्रिकोणमितीय पहचान के रूप में भी जाना जाता है। ये कार्य सही त्रिकोण के भीतर विशेष अनुपातों के साथ कोणों का निर्धारण करने में महत्वपूर्ण भूमिका निभाते हैं।

विपरीत त्रिकोणमितीय कार्य

• यदि Sin θ = x, तो θ = sin^-1 x = arcsin(x)
• समान रूप से, θ = cos^-1 x = arccos(x)
• θ = tan^-1 x = arctan(x)

• sin^-1(sin θ) = θ
• cos^-1(cos θ) = θ
• tan^-1(tan θ) = θ

विपरीत त्रिकोणमिति सूत्र

• sin^-1(–x) = – sin^-1 x
• cos^-1(–x) = π – cos^-1 x
• tan^-1(–x) = – tan^-1 x
• cosec^-1(–x) = – cosec^-1 x
• sec^-1(–x) = π – sec^-1 x
• cot^-1(–x) = π – cot^-1 x

डिग्री से रेडियन सूत्र यदि x एक कोण है डिग्री में और t एक कोण है रेडियन में, तो:

• π/180° = t/x ⇒ t = πx/180° और x = 180°t/x

साइन, कोसाइन और टैंगेंट का नियम

साइन का नियम एक त्रिकोण के भुजाओं के लम्बाई के अनुपातों को उसके कोणों के साइन से संबंधित करता है, यह बताते हुए कि एक कोण का साइन उसके विपरीत भुजा की लम्बाई द्वारा विभाजित किया गया एक समान रहता है।

sin α/a = sin β/b = sin γ/c

कोसाइन का नियम

कोसाइन का नियम एक त्रिकोणमितीय सूत्र है जिसका उपयोग गैर-सही त्रिकोणों में भुजाओं की लम्बाई का निर्धारण करने के लिए किया जाता है, जो एक भुजा के वर्ग को अन्य दो भुजाओं के वर्गों के योग से संबंधित करता है, जिसमें उनके लम्बाई का दो बार गुणन और शामिल कोण का कोसाइन घटाया जाता है।

a² = b² c² − 2bc cos α

b² = a² c² − 2ac cos β

c² = a² b² − 2ab cos γ

टैंगेंट का नियम

a − b/a b = tan½(α − β)/tan½(α β) b – c/ b c = tan½ (β − γ)/tan½(β γ) a – c/ a c = tan½ (α − γ)/tan½(α γ)

त्रिकोणमिति सूत्र उदाहरण

Q1: यदि sin2A का मान 1/2 है, तो sinAcosA का मान क्या होगा? समाधान: जैसा कि हम जानते हैं कि sin2A = 2sinAcosA दिया गया है, sin2A = 1/2 LHS पर sin2A का मान डालते हैं 2sinAcosA = 1/2 sinAcosA = (1/2) x (1/2) इस प्रकार, sinAcosA = 1/4

Q2: दिया गया है कि sin2A का मान 1 है। (sinA – cosA) का मान ज्ञात करें। समाधान: दिया गया है, sin2A = 1 जैसा कि हम जानते हैं, sin2A = 2sinAcosA हमें sinA – cosA का मान ज्ञात करना है (sinA – cosA) को वर्ग करते हैं, हमें मिलता है (sinA – cosA)² = sin²A + cos²A – 2sinAcosA चूंकि sin²A + cos²A = 1 और 2sinAcosA = sin2A इन मानों को उपरोक्त समीकरण में डालने पर हमें मिलता है => 1 – sin²A जैसा कि दिया गया है sin²A = 1 => 1-1 = 0 चूंकि (sinA – cosA)² = 0, sin A – cos A = √0 इस प्रकार, sinA – cosA = 0

Q3: समकोण त्रिकोण ABC में, जहाँ AC कर्ण है, sin A का मान 1/2 दिया गया है। cos C का मान क्या होगा? समाधान: दिया गया ABC एक समकोण त्रिकोण है। AC कर्ण है, तो B का मान 90° होना चाहिए। दिया गया है, sinA = 1/2 चूंकि sin 30° = 1/2 इसलिए, sinA = sin30 या, A = 30° तो, C का मान 90° – 30° = 60° है इस प्रकार, cosC = cos60 = 1/2

इसलिए, cosC का मान = 1/2

Q4: cos–1x का मुख्य मान ज्ञात करें, जब x=√3/2। समाधान: यदि cos–1(√3/2) = θ, तो cos θ = √3/2। चूंकि हम मुख्य शाखा पर विचार कर रहे हैं, θ ∈ [0 , π]। साथ ही, चूंकि √3/2 > 0 है, θ पहले चतुर्थ में होने पर, इसलिए cos–1 (√3/2) = π/6।