महत्वपूर्ण सूत्र: गति, समय और दूरी | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download

गति, समय और दूरी क्या हैं?

• गति: गति वह दर है, जिसके द्वारा एक वस्तु गति में एक विशेष दूरी को पार करती है।
• समय: समय दो घटनाओं के बीच का अंतराल है।
• दूरी: दूरी दो बिंदुओं के बीच की स्थान की माप है।

गति, समय और दूरी की इकाइयाँ

गति, दूरी और समय को विभिन्न इकाइयों में व्यक्त किया जा सकता है:

• समय को सामान्यतः सेकंड (s), मिनट (min) और घंटे (hr) में व्यक्त किया जा सकता है।
• जबकि दूरी को सामान्यतः मीटर (m), किलोमीटर (km), सेंटीमीटर, मील, फीट, आदि में व्यक्त किया जाता है।
• गति को सामान्यतः m/s, km/hr में व्यक्त किया जाता है।

उदाहरण: यदि दूरी किलोमीटर में दी गई है और समय घंटे में है, तो सूत्र के अनुसार: गति = दूरी / समय; गति की इकाई किलोमीटर/ घंटे (km/hr) हो जाएगी।

गति, समय और दूरी के बीच संबंध

अब जब हम गति, दूरी और समय की परिभाषा से अच्छी तरह परिचित हैं, तो चलिए इनके बीच के संबंध को समझते हैं। गति, समय और दूरी तीन चर हैं जो गति का गणितीय मॉडल प्रस्तुत करते हैं।

• समय सीधे दूरी के आनुपातिक है। इसका अर्थ है कि यदि हमारे पास दो वाहन हैं जो दो विभिन्न समय अवधि के लिए दो दूरी पर चल रहे हैं, तो समय दूरी के सीधे आनुपातिक है।
• गति सीधे दूरी के आनुपातिक है। इसका अर्थ है कि यदि हमारे पास दो वाहन हैं जो दो विभिन्न गति पर दो दूरी पर चल रहे हैं, तो समय स्थिर रहता है।
• गति समय के विपरीत आनुपातिक है। इसका अर्थ है कि यदि हमारे पास दो वाहन हैं जो दो विभिन्न गति पर चल रहे हैं और क्रमशः समय ले रहे हैं, तो दूरी स्थिर रहती है।

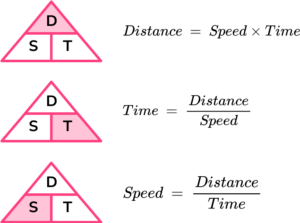
गति की गणना के लिए सूत्र:

गति = दूरी / समय

यह हमें बताता है कि एक लक्ष्य कितना धीमा या तेज़ चलता है। यह कवर की गई दूरी को कवर करने के लिए आवश्यक समय से विभाजित करके दर्शाता है।

गति सीधे दिए गए दूरी के अनुपात में और प्रस्तावित समय के विपरीत अनुपात में होती है। इस प्रकार,

दूरी = गति x समय

समय = दूरी / गति

जैसे-जैसे गति बढ़ती है, आवश्यक समय कम होगा और इसके विपरीत।

गति, समय और दूरी का परिवर्तन

(i) गति का परिवर्तन

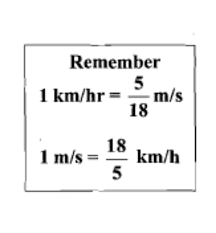
किसी दिए गए डेटा को किमी/घंटा से मी/सेकंड में बदलने के लिए, हम इसे 5/18 से गुणा करते हैं। क्योंकि 1 किमी/घंटा = 5/18 मी/सेकंड। इसी तरह, किसी दिए गए डेटा को मी/सेकंड से किमी/घंटा में बदलने के लिए, हम इसे 18/5 से गुणा करते हैं। क्योंकि 1 मी/सेकंड = 18/5 किमी/घंटा = 3.6 किमी/घंटा।

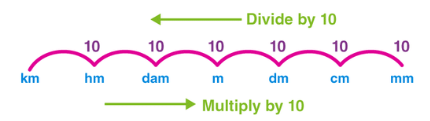
(ii) दूरी का परिवर्तन

एक बड़े यूनिट को छोटे यूनिट में बदलने के लिए, हम गुणा करते हैं। छोटे यूनिट को बड़े यूनिट में बदलने के लिए, हम विभाजित करते हैं। दूरी में परिवर्तन निम्नलिखित हैं:

इसी तरह, कुछ अन्य परिवर्तन नीचे दिए गए हैं:

• 1 किमी/घंटा = 5/8 मील/घंटा
• 1 गज = 3 फीट
• 1 किलोमीटर = 1000 मीटर
• 1 मील = 1.609 किलोमीटर
• 1 घंटा = 60 मिनट = 3600 सेकंड
• 1 मील = 1760 गज
• 1 गज = 3 फीट
• 1 मील = 5280 फीट

(iii) समय का परिवर्तन

(i) घंटों को मिनटों में और इसके विपरीत कैसे बदलें?

घंटों को मिनटों में बदलने के लिए एक सरल सूत्र का उपयोग किया जा सकता है: मिनटों की संख्या = (दिए गए घंटे की संख्या x 60) मिनट। इसी तरह, मिनटों को घंटों में बदलने के लिए = (मिनटों की संख्या/60) घंटे।

(ii) मिनटों को सेकंड में और इसके विपरीत कैसे परिवर्तित करें?

मिनटों को सेकंड में परिवर्तित करने का सूत्र इस प्रकार है:

सेकंडों की संख्या = (दी गई संख्या के मिनट x 60) सेकंड

इसी प्रकार, सेकंड को मिनट में परिवर्तित करने का सूत्र है = (सेकंडों की संख्या/60) मिनट

गति, समय और दूरी के अनुप्रयोग

गति, समय और दूरी के कुछ प्रमुख अनुप्रयोग निम्नलिखित हैं:

• औसत गति: औसत गति का निर्धारण इस सूत्र से किया जाता है = (कुल यात्रा की गई दूरी)/(कुल लिया गया समय)।
• प्रकरण 1 – जब यात्रा की गई दूरी स्थिर होती है और दो गति दी जाती हैं, तब:

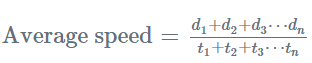
• प्रकरण 2 – जब लिया गया समय स्थिर होता है, तब औसत गति का निर्धारण इस सूत्र से किया जाता है:

उदाहरण: एक व्यक्ति एक स्थान से दूसरे स्थान पर 40 किमी/घंटा की गति से जाता है और 160 किमी/घंटा की गति से लौटता है। यदि कुल समय 5 घंटे है, तो दूरी प्राप्त करें।

हल: यहाँ दूरी स्थिर है, इसलिए लिया गया समय गति के विपरीत अनुपात में होगा। गति का अनुपात 40:160 है, अर्थात 1:4। इसलिए, लिया गया समय का अनुपात 4:1 होगा। कुल समय 5 घंटे है; इसलिए यात्रा करते समय समय 4 घंटे है और लौटते समय 1 घंटे का है। इसलिए, दूरी = 40 x 4 = 160 किमी।

प्रकरण 3 - यदि किसी दी गई दूरी का पहला भाग v1 की दर से समय t1 में और दूरी का दूसरा भाग v2 की दर से समय t2 में कवर किया जाता है, तो औसत गति इस सूत्र द्वारा दी जाती है:

सापेक्ष गति

जैसा कि नाम से पता चलता है, यह विचार दो या अधिक वस्तुओं के बीच की सापेक्ष गति के बारे में है। सापेक्ष गति का मूल सिद्धांत यह है कि जब वस्तुएँ एक-दूसरे के विपरीत दिशा में चलती हैं, तो गति को जोड़ा जाता है और जब वस्तुएँ समान दिशा में चलती हैं, तो गति को घटाया जाता है।

(i) उदाहरण के लिए, यदि दो यात्री ट्रेनें विपरीत दिशा में क्रमश: X किमी प्रति घंटे और Y किमी प्रति घंटे की गति से चल रही हैं। तो उनकी सापेक्ष गति निम्नलिखित सूत्र द्वारा दी जाती है:

सापेक्ष गति = X + Y

(ii) दूसरी ओर, यदि दोनों ट्रेनें समान दिशा में क्रमश: X किमी प्रति घंटे और Y किमी प्रति घंटे की गति से यात्रा कर रही हैं। तो उनकी सापेक्ष गति निम्नलिखित सूत्र द्वारा दी जाती है:

सापेक्ष गति = X - Y

पहले मामले के लिए, एक-दूसरे को पार करने में ट्रेन द्वारा लिया गया समय निम्नलिखित सूत्र द्वारा दिया जाता है:

सापेक्ष गति = X + Y

दूसरे मामले के लिए, एक-दूसरे को पार करने में ट्रेनों द्वारा लिया गया समय निम्नलिखित सूत्र द्वारा दिया जाता है:

सापेक्ष गति = X - Y

यहाँ L1, L2 क्रमश: ट्रेनों की लंबाई हैं।

गति और समय का प्रतिलोम अनुपात: जब दूरी स्थिर होती है, तो गति को समय के प्रतिलोम अनुपात में कहा जाता है। गणितीय रूप में, S 1/T के प्रतिलोम अनुपात में होता है जब D स्थिर है। ऐसी स्थिति में यदि गति का अनुपात m:n है, तो लिया गया समय अनुपात n:m में होगा।

प्रश्नों को हल करने के दो दृष्टिकोण हैं:

• प्रतिलोम अनुपात का प्रयोग
• स्थायी उत्पाद नियम का प्रयोग

उदाहरण: 100 किमी चलने के बाद, एक ट्रेन एक दुर्घटना का सामना करती है और सामान्य गति के (3/4) भाग पर चलती है और 55 मिनट देर से पहुँचती है। यदि दुर्घटना 20 किमी आगे होती, तो यह 45 मिनट देर से पहुँचती। सामान्य गति ज्ञात करें।

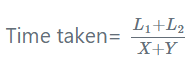
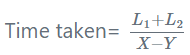
समाधान: विपरीत अनुपात विधि का अनुप्रयोग

यहाँ दो मामले हैं:

• मामला 1: दुर्घटना 100 किमी पर होती है।
• मामला 2: दुर्घटना 120 किमी पर होती है।

दो घटनाओं के बीच का अंतर केवल 20 किमी है जो 100 किमी और 120 किमी के बीच है। 10 मिनट का समय का अंतर केवल इन 20 किमी के कारण है। मामले 1 में, 100 किमी और 120 किमी के बीच 20 किमी को (3/4) गति पर कवर किया गया है। मामले 2 में, 100 किमी और 120 किमी के बीच 20 किमी सामान्य गति पर पहुँचा गया है। इसलिए 20 किमी को कवर करने के लिए सामान्य समय “t” निम्नलिखित तरीके से पाया जा सकता है:

• 4/3 t – t = 10 मिनट
• => t = 30 मिनट
• d = 20 किमी, इसलिए सामान्य गति = 20/30 मिनट = 20/0.5 = 40 किमी/घंटा

स्थायी उत्पाद नियम विधि का उपयोग करते हुए: मान लीजिए कि वास्तविक समय T के बराबर है। गति में (1/4) की कमी होने पर, इससे समय में (1/3) की वृद्धि होगी क्योंकि गति और समय एक-दूसरे के विपरीत अनुपात में होते हैं। यदि एक पैरामीटर में 1/x की वृद्धि होती है, तो दूसरे पैरामीटर में 1/(x+1) की कमी होगी यदि पैरामीटर विपरीत अनुपात में हैं। इस कमी के कारण होने वाली देरी 10 मिनट है। इसलिए, 1/3 T = 10 और T = 30 मिनट या 0.5 घंटा। दूरी = 20 किमी, इस प्रकार गति = 40 किमी/घंटा।

मिलने का बिंदु प्रश्न:

यदि दो व्यक्ति स्थान P और Q से एक-दूसरे की ओर यात्रा करते हैं और वे बिंदु X पर मिलते हैं। तब उनके द्वारा मिलन के समय कुल दूरी PQ होगी। दोनों के मिलने में लगने वाला समय समान होगा। चूंकि समय स्थिर है, PX और QX की दूरी उनकी गति के अनुपात में होगी। मान लीजिए कि P और Q के बीच की दूरी d है। यदि दो व्यक्ति क्रमशः P और Q से एक-दूसरे की ओर बढ़ते हैं, जब वे पहली बार मिलते हैं, तो वे कुल मिलाकर “d” दूरी कवर करते हैं। जब वे दूसरी बार मिलते हैं, तो वे आपस में “3d” दूरी कवर करते हैं। इसी तरह, जब वे तीसरी बार मिलते हैं, तो वे संयुक्त रूप से “5d” दूरी कवर करते हैं और यह प्रक्रिया चलती रहती है।

अंकित और अरNav को अपने-अपने वाहनों से दिल्ली से हैदराबाद जाना है। अंकित 80 किमी/घंटा की गति से चल रहा है जबकि अरNav 120 किमी/घंटा की गति से। यदि अंकित को पहुँचने में 9 घंटे लगते हैं, तो अरNav को हैदराबाद पहुँचने में कितना समय लगेगा?

समाधान: जैसा कि हम देख सकते हैं कि दोनों मामलों में तय की गई दूरी समान है, समय की अवधि गति के विपरीत अनुपात में होगी। दिए गए प्रश्न में, अंकित और अरNav की गति का अनुपात 80:120 या 2:3 है। इसलिए अंकित द्वारा लिए गए समय का अनुपात अरNav द्वारा लिए गए समय के साथ 3:2 रहेगा। इस प्रकार, यदि अंकित को 9 घंटे लगते हैं, तो अरNav को 6 घंटे लगेंगे।

गति, समय और दूरी के सूत्र

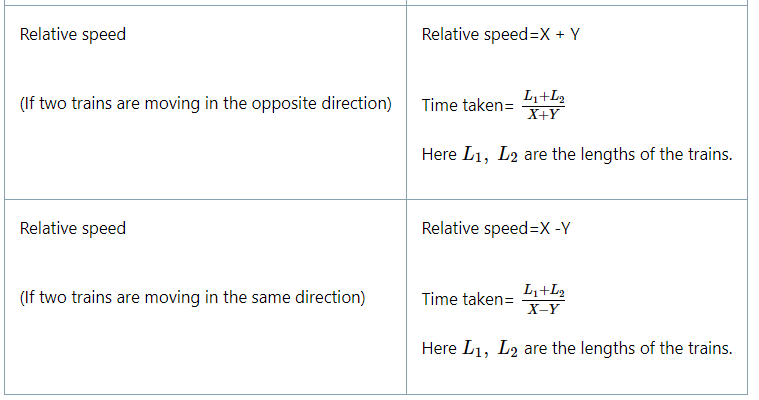
गति, दूरी और समय के कुछ अतिरिक्त सूत्र इस प्रकार हैं:

• यदि P और Q की गति का अनुपात p:q है, तो समान दूरी तक पहुँचने में उनके द्वारा खर्च किए गए समय का अनुपात 1/p:1/q या q:p है।
• यदि दो व्यक्ति या वाहन या ट्रेन एक ही समय में दो बिंदुओं A और B से विपरीत दिशा में शुरू करते हैं और एक-दूसरे को पार करने के बाद यात्रा समाप्त करने में क्रमशः समय a और b लेते हैं, तो गति का अनुपात निम्नलिखित सूत्र द्वारा दिया जाता है:

• यदि दो व्यक्ति दो अलग-अलग गति x और y के साथ समान दूरी तय करते हैं और विपरीत दिशाओं में जाते हैं। जहाँ कुल समय दिया गया है और दूरी पूछी गई है, तो सूत्र इस प्रकार है:

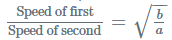
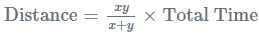
गति, समय और दूरी से संबंधित प्रश्नों के प्रकार

गति, समय और दूरी से संबंधित कुछ विशिष्ट प्रकार के प्रश्न हैं जो आमतौर पर परीक्षाओं में आते हैं। गति, दूरी और समय से संबंधित कुछ महत्वपूर्ण प्रश्नों के प्रकार निम्नलिखित हैं:

(क) ट्रेन से संबंधित समस्याएँ

कृपया ध्यान दें कि ट्रेन की समस्याओं के मामले में, किसी वस्तु को पार करते समय तय की जाने वाली दूरी निम्नलिखित होती है:

• तय की जाने वाली दूरी = ट्रेन की लंबाई + वस्तु की लंबाई

याद रखें कि यदि विचाराधीन वस्तु एक पोल, व्यक्ति या बिंदु है, तो हम उन्हें शून्य लंबाई वाली बिंदु वस्तुओं के रूप में मान सकते हैं। इसका अर्थ है कि हम इन वस्तुओं की लंबाई पर विचार नहीं करेंगे। हालाँकि, यदि विचाराधीन वस्तु एक प्लेटफॉर्म (गैर-बिंदु वस्तु) है, तो इसकी लंबाई तय की जाने वाली दूरी के सूत्र में जोड़ी जाएगी।

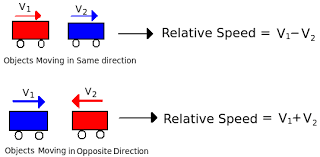
(ख) नावें और धाराएँ

ऐसी समस्याओं में, नावें या तो धारा की दिशा में या धारा के विपरीत दिशा में चलती हैं। धारा के साथ नाव की दिशा को डाउनस्ट्रीम कहा जाता है और धारा के खिलाफ नाव की दिशा को अपस्ट्रीम कहा जाता है।

यदि पानी में नाव की गति u किमी/घंटा है और धारा की गति v किमी/घंटा है, तो:

• (1) डाउनस्ट्रीम गति = (u + v) किमी/घंटा
• (2) अपस्ट्रीम गति = (u – v) किमी/घंटा

टिप्स और ट्रिक्स

टिप्स और ट्रिक्स

हम गति, समय और दूरी पर आधारित प्रश्नों को हल करने के लिए विभिन्न टिप्स और ट्रिक्स नीचे पा सकते हैं।

• टिप 1: सापेक्ष गति को दूसरे शरीर के संबंध में एक चलित शरीर की गति के रूप में परिभाषित किया गया है। सापेक्ष गति के संभावित मामले हैं:
  • एक ही दिशा: जब दो शरीर एक ही दिशा में चल रहे होते हैं, तो सापेक्ष गति उनकी गति के बीच का अंतर होती है और इसे हमेशा एक सकारात्मक मान के रूप में व्यक्त किया जाता है।
  • विपरीत दिशा: जब दो शरीर विपरीत दिशा में चल रहे होते हैं, तो सापेक्ष गति उनकी गति का योग होती है।
• टिप 2: औसत गति = कुल दूरी / कुल समय
• टिप 3: जब ट्रेन एक चलती हुई वस्तु को पार करती है, तो:
  • 1) यदि दोनों एक ही दिशा में चल रहे हैं, तो सापेक्ष गति = दोनों गति का अंतर
  • 2) यदि दोनों विपरीत दिशा में चल रहे हैं, तो सापेक्ष गति = दोनों गति का योग
• टिप 4: ट्रेन एक लंबे वस्तु या प्लेटफ़ॉर्म को पार करते समय, जब एक ट्रेन एक प्लेटफ़ॉर्म या लंबे वस्तु को पार करती है, तो ट्रेन द्वारा पार की गई दूरी उस वस्तु की लंबाई और ट्रेन की लंबाई का योग होगी।
• टिप 5: ट्रेन एक आदमी या बिंदु वस्तु को पार करते समय, जब एक ट्रेन एक आदमी/वस्तु को पार करती है, तो ट्रेन द्वारा पार की गई दूरी उस वस्तु की लंबाई के बराबर होगी।

गति, समय और दूरी के हल किए गए उदाहरण

उदाहरण 1: तीन कारों की गति का अनुपात 5 : 4 : 6 है। समान दूरी तय करने में उनके द्वारा लिए गए समय का अनुपात ________ है। समाधान: चूंकि गति और समय उल्टे संबंध का पालन करते हैं,

गति = दूरी / समय

समय लेने के अनुपात = 1/5 : 1/4 : 1/6 = 12 : 15 : 10

उदाहरण 2: एक नाव को 20 किमी नीचे की तरफ जाने में 40 मिनट लगते हैं। यदि धारा की गति 2.5 किमी/घंटा है, तो वापस आने में इसे और कितना समय लगेगा?

हल: नीचे जाने का समय = 40 मिनट = 40/60 = 2/3 घंटे। नीचे की गति = 20/ (2/3) = 30 किमी/घंटा। जैसा कि हम जानते हैं, धारा की गति = 1/2 × (नीचे की गति – ऊपर की गति) ⇒ ऊपर की गति = 30 – 2 × 2.5 = 30 – 5 = 25 किमी/घंटा। वापस आने में लगने वाला समय = 20/25 = 0.8 घंटे = 0.8 × 60 = 48 मिनट। ∴ नाव को वापस आने में = 48 – 40 = 8 मिनट अधिक लगेंगे।

उदाहरण 3: दो ट्रेनें एक ही दिशा में क्रमशः 43 किमी/घंटा और 51 किमी/घंटा की गति से चल रही हैं। तेज ट्रेन द्वारा धीमी ट्रेन में बैठे एक आदमी को पार करने में लगने वाला समय 72 सेकंड है। तेज ट्रेन की लंबाई (मीटर में) क्या है?

हल: दिए गए: 2 ट्रेनों की गति = 43 किमी/घंटा और 51 किमी/घंटा। दोनों ट्रेनों की सापेक्ष गति = (51 – 43) किमी/घंटा = 8 किमी/घंटा। सापेक्ष गति को मीटर/सेकंड में = 8 × (5/18) मीटर/सेकंड ⇒ 72 सेकंड में ट्रेन द्वारा तय की गई दूरी = 8 × (5/18) × 72 = 160। इसलिए, तेज ट्रेन की लंबाई = 160 मीटर।