महत्वपूर्ण नोट्स: गति, दूरी और समय | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download

परिचय

• गति, दूरी और समय विभिन्न प्रतियोगी परीक्षाओं में सबसे सामान्यत: परीक्षण किए जाने वाले विषयों में से एक है। इस विषय से प्रश्न पिछले कई वर्षों से विभिन्न परीक्षाओं में लगातार पूछे जाते रहे हैं।
• प्रतियोगी परीक्षाएं न केवल इस विचार में सूत्रीय ज्ञान की जांच करती हैं, बल्कि इसमें शामिल अवधारणाओं के मजबूत मूलभूत सिद्धांतों और उनके अनुप्रयोग की भी जांच करती हैं। उदाहरण के लिए, दौड़ें एक विचार के रूप में गति, समय और दूरी के साथ-साथ अनुपात और अनुपातों पर आधारित होती हैं।

किसी वस्तु की गति वह दूरी है जो वस्तु द्वारा प्रति इकाई समय में तय की जाती है, अर्थात्, गति = दूरी/समय।

• गति: गति वह दर है जिस पर एक वस्तु गति में एक विशेष दूरी को तय करती है।
• समय: समय दो घटनाओं के बीच का अंतराल है।
• दूरी: दूरी दो बिंदुओं के बीच के स्थान की मात्रा है।

गति, समय और दूरी की इकाइयाँ

गति, दूरी और समय प्रत्येक को विभिन्न इकाइयों में व्यक्त किया जा सकता है:

• समय को सामान्यतः सेकंड (s), मिनट (min) और घंटे (hr) के रूप में व्यक्त किया जा सकता है।
• जबकि दूरी को आमतौर पर मीटर (m), किलोमीटर (km), सेंटीमीटर (cm), मील, फीट (ft) आदि के रूप में व्यक्त किया जाता है।
• गति सामान्यतः मीटर प्रति सेकंड (m/s) और किलोमीटर प्रति घंटे (km/hr) में व्यक्त की जाती है।

उदाहरण: यदि दूरी किलोमीटर (km) में दी गई है और समय घंटे (hr) में है, तो सूत्र के अनुसार: गति = दूरी / समय; गति की इकाई किलोमीटर प्रति घंटे (km/hr) हो जाएगी।

गति, समय और दूरी के बीच संबंध

अब जब हम गति, दूरी और समय की परिभाषा से अच्छी तरह परिचित हैं, तो आइए समझते हैं कि इनके बीच संबंध क्या है। कहा जाता है कि एक वस्तु तब गति या चलन प्राप्त करती है जब यह किसी बाहरी स्थिर बिंदु के सापेक्ष अपनी स्थिति बदलती है। गति, समय और दूरी ये तीन चर हैं जो गति के गणितीय मॉडल का प्रतिनिधित्व करते हैं, जैसे कि, s x t = d।

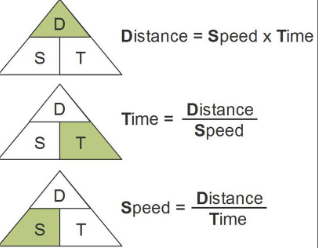
• समय सीधे दूरी के समानुपाती है। इसका अर्थ है कि यदि हमारे पास दो वाहन हैं जो दो अलग-अलग समय अवधि के लिए दो दूरी तय कर रहे हैं, तो समय सीधे दूरी के समानुपाती है।
• गति सीधे दूरी के समानुपाती है। इसका अर्थ है कि यदि हमारे पास दो वाहन हैं जो दो अलग-अलग गति पर दो दूरी तय कर रहे हैं, तो समय स्थिर रहता है।
• गति समय के विपरीत समानुपाती है। इसका अर्थ है कि यदि हमारे पास दो वाहन हैं जो दो अलग-अलग गति पर चल रहे हैं और क्रमशः समय ले रहे हैं, तो दूरी स्थिर रहती है।

गति, समय और दूरी का रूपांतरण

गति, समय और दूरी को विभिन्न इकाइयों में परिवर्तित करने की प्रक्रिया निम्नलिखित है:

• किसी दिए गए डेटा को km/घंटा से m/सेकंड में परिवर्तित करने के लिए, हम 5/18 से गुणा करते हैं। क्योंकि 1 km/घंटा = 5/18 m/सेकंड।
• किसी दिए गए डेटा को m/सेकंड से km/घंटा में परिवर्तित करने के लिए, हम 18/5 से गुणा करते हैं। क्योंकि 1 m/सेकंड = 18/5 km/घंटा = 3.6 km/घंटा।

सूत्र के संदर्भ में, हम इसे इस प्रकार सूचीबद्ध कर सकते हैं:

• 1 km/hr = 5/8 मील/घंटा
• 1 गज = 3 फीट
• 1 किलोमीटर = 1000 मीटर
• 1 मील = 1.609 किलोमीटर
• 1 घंटा = 60 मिनट = 3600 सेकंड
• 1 मील = 1760 गज
• 1 गज = 3 फीट
• 1 मील = 5280 फीट

गति, समय और दूरी के अनुप्रयोग

गति, समय और दूरी के कुछ अनुप्रयोग निम्नलिखित हैं:

1. औसत गति

• औसत गति को निम्नलिखित सूत्र द्वारा निर्धारित किया जाता है = (कुल यात्रा की गई दूरी)/(कुल समय लिया गया)।
• जब यात्रा की गई दूरी स्थिर होती है और दो गति दी गई होती हैं, तो औसत गति को इन दोनों गति के हार्मोनिक माध्य के सूत्र का उपयोग करके गणना की जा सकती है: जहाँ x और y वे दो गति हैं जिन पर संबंधित दूरी पहुँची गई है। यह सूत्र काम करता है क्योंकि यात्रा के प्रत्येक चरण के लिए लिया गया समय गति के विपरीत आनुपातिक होता है।

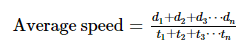
2. सापेक्ष गति

सापेक्ष गति का मूल सिद्धांत यह है कि गति विपरीत दिशा में चल रहे वस्तुओं के मामले में मिलकर जुड़ जाती है और समान दिशा में चल रहे वस्तुओं के मामले में गति घटाई जाती है।

(क) यदि दो वस्तुएं विपरीत दिशा में चल रही हैं

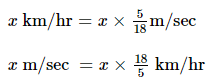
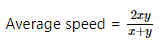
सापेक्ष गति = X + Y
ट्रेनें एक-दूसरे को पार करने में जो समय लेती हैं, वह निम्नलिखित सूत्र द्वारा दिया गया है: यहाँ L1 और L2 क्रमशः ट्रेनों की लंबाई हैं।

• सापेक्ष गति = X + Y

• यहाँ L1 और L2 क्रमशः ट्रेनों की लंबाई हैं।

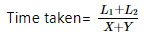
(b) यदि दो वस्तुएं समान दिशा में चल रही हैं

• सापेक्ष गति = X - Y
  ट्रेनें एक-दूसरे को पार करने में जो समय लेती हैं, वह निम्नलिखित सूत्र द्वारा दिया गया है: यहाँ L1 और L2 क्रमशः ट्रेनों की लंबाई हैं।

• यहाँ L1 और L2 क्रमशः ट्रेनों की लंबाई हैं।

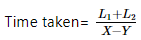
3. सीधी रेखा में गति

सीधी रेखा में गति की स्थितियों पर समस्याएं CAT और अन्य योग्यता परीक्षाओं में सबसे सामान्य पूछे जाने वाले प्रश्नों में से एक हैं। इसलिए निम्नलिखित सिद्धांतों की उचित समझ और समस्या समाधान में उनके अनुप्रयोग के लिए छात्रों के लिए यह अत्यंत महत्वपूर्ण होगा। सीधी रेखा में गति सापेक्ष गति के नियमों द्वारा नियंत्रित होती है।

कई या अधिक वस्तुएं एक ही बिंदु से शुरू होकर समान दिशा में चल रही हैं: उनकी सापेक्ष गति S1 - S2 है।

(a) यदि वस्तुएं दो बिंदुओं A और B के बीच आगे-पीछे चल रही हैं:

• तेज़ वस्तु पहले अंत तक पहुँचेगी और रास्ते में दूसरी वस्तु से मिलेगी।
• सापेक्ष गति S1 - S2 तब तक लागू होगी जब तक वस्तु का परिवर्तन बिंदु नहीं आ जाता और उसके बाद दोनों वस्तुएँ S1 + S2 की सापेक्ष गति से विपरीत दिशाओं में चलने लगेंगी।
• दोनों वस्तुओं द्वारा तय की गई कुल दूरी = 2D

(b) यदि वस्तुएं बिना किसी अंत बिंदु पर पहुँचने और दिशा बदलने के समान दिशा में चलना जारी रखें:

• तेज़ गति वाला शरीर आगे बढ़ेगा और अपनी बढ़त बनाए रखेगा और दोनों शरीरों की गति सापेक्ष गति समीकरण S1 - S2 द्वारा संचालित होगी।

विपरीत दिशा में गति करना: उनकी सापेक्ष गति प्रारंभ में S1 S2 द्वारा दी जाएगी।

(क) जब दोनों शरीर दो बिंदुओं A और B के बीच इधर-उधर चलते हैं और मार्ग के विपरीत छोरों से शुरू होते हैं:

• दोनों शरीर एक-दूसरे की ओर बढ़ेंगे, A और B के बीच एक बिंदु पर मिलेंगे, फिर एक-दूसरे से दूर चले जाएंगे। तेज़ गति वाला शरीर पहले अपने चरम बिंदु पर पहुंचेगा, उसके बाद धीमा शरीर अपने चरम बिंदु पर पहुंचेगा। मिलने का बिंदु शरीरों की गति के अनुपात द्वारा निर्धारित होगा।

(ख) जब शरीर एक ही दिशा में आगे बढ़ता है बिना किसी अंत बिंदु पर पहुंचने और दिशा बदलने के:

• सापेक्ष गति प्रारंभ में S1 S2 होगी जब शरीर एक-दूसरे के करीब आ रहे होंगे और जब दूर जा रहे होंगे।

उदाहरण 1: दो शरीर A और B सीधी सड़क के विपरीत छोर P और Q से शुरू होते हैं। वे एक बिंदु 0.6D पर P से मिलते हैं। उनका चौथे मिलने का बिंदु क्या होगा?

समाधान: चूंकि समय स्थिर है, हमारे पास गति का अनुपात 3:2 है। इसके अलावा, चौथे मिलने के लिए दोनों द्वारा कुल दूरी 7D तय करनी है। यह दूरी 3:2 के अनुपात में विभाजित होती है। इसलिए, A 4.2D और B 2.8D तय करेगा। चौथे मिलने के बिंदु को A या B की गति को ट्रैक करके पाया जा सकता है। A, जिसने 4.2D की दूरी तय की है, P से 0.2D पर होगा। यही आवश्यक उत्तर है।

उदाहरण 2: A एक स्थान से एक निश्चित दिशा में 2 किमी/घंटा की समान गति से चलना शुरू करता है। आधे घंटे बाद, B उसी स्थान से निकलता है और A की समान दिशा में समान गति से चलता है और 1 घंटा 48 मिनट में A को पीछे छोड़ देता है। B की गति की गणना करें?

हल: पहले दो वाक्यों से, आप देख सकते हैं कि जब B चलना शुरू करता है, तब A B से 1 किमी आगे है। यह 1 किमी का अंतराल B द्वारा 9/5 घंटे में कवर किया गया है। यहाँ कार्यात्मक समीकरण (SB-SA) x T = प्रारंभिक दूरी है। (SB - 2) x 9/5 = 1। हल करने पर, हमें SB = 23/9 किमी/घंटा मिलता है।

त्वरण का सिद्धांत

• त्वरण को 'गति में परिवर्तन की दर' के रूप में परिभाषित किया जाता है।
• त्वरण सकारात्मक, शून्य या नकारात्मक हो सकता है।
• जब त्वरण नकारात्मक होता है, तो इसे कम गति कहा जाता है।
• त्वरण की इकाई m/s² है।
• समीकरण (i) त्वरण = गति / समय (ii) अंतिम गति = प्रारंभिक गति + त्वरण x समय

उदाहरण: पानी एक सिलिंड्रिकल बीकर में एक स्थिर दर पर बहता है। बीकर का आधार क्षेत्र 24 सेमी² है। पानी का स्तर हर सेकंड में 10 सेमी बढ़ता है। 30 सेमी² के आधार क्षेत्र वाले बीकर में पानी का स्तर कितनी तेजी से बढ़ेगा?

• समीकरण (i) त्वरण = गति / समय (ii) अंतिम गति = प्रारंभिक गति + त्वरण x समय

हल: बीकर में पानी का प्रवाह = 24 सेमी² x 10 सेमी/सेकंड = 240 सेमी³/सेकंड। यदि आधार क्षेत्र 30 सेमी² है, तो पानी के स्तर की वृद्धि की दर होगी 240/30 = 8 सेमी/सेकंड।

गति, समय और दूरी के सूत्र

कुछ महत्वपूर्ण गति, दूरी और समय के सूत्र नीचे दिए गए हैं:

• यदि P और Q की गति का अनुपात p: q है, तो एक ही दूरी तक पहुँचने के लिए उनके द्वारा उपयोग किए गए समय का अनुपात 1/p:1/q या q: p होगा।
• यदि दो व्यक्ति, वाहन या ट्रेन एक ही समय में A और B से विपरीत दिशा में शुरू करते हैं और एक-दूसरे को पार करने के बाद यात्रा समाप्त करने में क्रमशः समय a और b लेते हैं, तो गति का अनुपात निम्नलिखित सूत्र द्वारा दिया जाता है:
• यदि दो व्यक्ति अलग-अलग गति x और y के साथ एक ही दूरी तय करते हैं और वे विपरीत दिशाओं में यात्रा करते हैं। जहां कुल समय दिया गया है और दूरी पूछी गई है, तो सूत्र है:

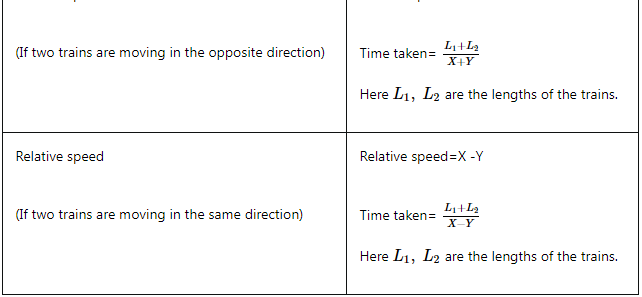
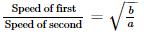
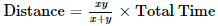
गति, समय और दूरी से प्रश्नों के प्रकार

गति, समय और दूरी से कुछ विशेष प्रकार के प्रश्न होते हैं जो आमतौर पर परीक्षाओं में आते हैं। गति, दूरी और समय से कुछ महत्वपूर्ण प्रकार के प्रश्न निम्नलिखित हैं।

1. ट्रेनें

• ट्रेन समस्याओं के मामले में, किसी वस्तु को पार करते समय तय की जाने वाली दूरी = ट्रेन की लंबाई + वस्तु की लंबाई।
• यदि विचाराधीन वस्तु एक पोल, व्यक्ति या बिंदु है, तो हम उन्हें शून्य लंबाई वाली बिंदु वस्तुएं मान सकते हैं। इसका मतलब है कि हम इन वस्तुओं की लंबाई को नहीं मानेंगे। हालांकि, यदि विचाराधीन वस्तु एक प्लेटफॉर्म (गैर-बिंदु वस्तु) है, तो इसकी लंबाई को तय की जाने वाली दूरी के सूत्र में जोड़ा जाएगा।

व्याख्या: A-B, A-C, C-B के बीच की दूरी क्रमशः 180, 120 और 60 किमी है। मान लें कि x वह दूरी है जहाँ 2 ट्रेनें मिलती हैं। दिए गए स्थिति के अनुसार हमारे पास है:

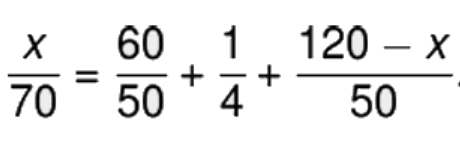
समीकरण को सुलझाने पर हमें x लगभग 112 किमी मिलता है।

2. नावें और धाराएँ

जब नाव और नदी की धारा (या प्रवाह) एक ही दिशा में चलते हैं, तो नाव की सापेक्ष गति नाव और नदी की गति का योग होती है। इसे \"डाउनस्ट्रीम स्पीड\" कहा जाता है।

जब नाव धाराओं के प्रवाह के खिलाफ जाती है, या विपरीत दिशा में, तो इसकी गति इसकी गति और धारा की गति का अंतर होती है। इसे \"अपस्ट्रीम स्पीड\" कहा जाता है।

मान लें कि B स्थिर जल में नाव की गति है और C नदी के प्रवाह की गति है। यदि B>C; डाउनस्ट्रीम स्पीड D = (B + C) अपस्ट्रीम स्पीड U = (B – C) जब एक नाव द्वारा अपस्ट्रीम (पानी के प्रवाह के खिलाफ) तय की गई दूरी वही होती है जो वह डाउनस्ट्रीम (पानी के प्रवाह के साथ) तय करती है। उदाहरण: दो नावें, जो क्रमशः 5 किमी/घंटा और 10 किमी/घंटा की गति से यात्रा कर रही हैं, सीधे एक-दूसरे की ओर बढ़ती हैं। वे एक दूसरे से 20 किमी की दूरी पर शुरू होती हैं। वे टकराने से एक मिनट पहले (किमी में) कितनी दूर हैं? (क) 1/12 (ख) 1/6 (ग) 1/4 (घ) 1/3

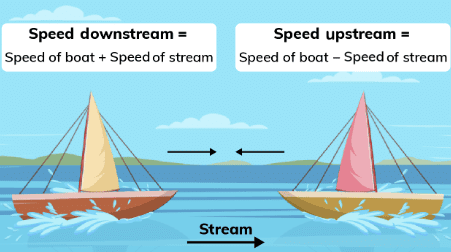
मान लें कि B स्थिर जल में नाव की गति है और C नदी के प्रवाह की गति है। यदि B>C; डाउनस्ट्रीम स्पीड D = (B + C) अपस्ट्रीम स्पीड U = (B – C)

उदाहरण: दो नावें, जो 5 किमी/घंटा और 10 किमी/घंटा की गति से चल रही हैं, एक-दूसरे की ओर सीधे बढ़ रही हैं। वे एक-दूसरे से 20 किमी की दूरी पर शुरू होती हैं। वे टकराने से एक मिनट पहले कितनी दूर हैं (किमी में)? (क) 1/12 (ख) 1/6 (ग) 1/4 (घ) 1/3

हल: विकल्प 'ग' सही है। स्पष्टीकरण: टकराने से ठीक पहले, अंतिम मिनट में। नाव संख्या 1 ने यात्रा की = 5 x 1/60 = 1/12 किमी नाव संख्या 2 ने यात्रा की = 10 x 1/60 = 1/6 किमी चूंकि वे विपरीत दिशाओं में चल रही हैं, टकराने से एक मिनट पहले नावों के बीच की दूरी है 1/12 + 1/6 = 1/4 किमी

3. दौड़ें

3. दौड़ें

(i) स्टार्टअप या हेडस्टार्ट - जब एक धावक दूसरे धावक को उसी दौड़ में आगे रहने देता है, तो इसे दौड़ में स्टार्टअप कहा जाता है। (ii) डेड हीट - जब दो या दो से अधिक धावक एक ही समय में फिनिश लाइन को पार करते हैं, तो उन्हें "डेड हीट" में "फिनिश" करने के लिए माना जाता है।

कुछ और उपयोगी अवधारणाएँ

• जब कहा जाता है कि A, B को एक दौड़ में x मीटर का स्टार्ट दे सकता है, इसका मतलब है कि समान समय में, B, A से x मीटर कम दौड़ता है।
• एक दौड़ में y मीटर, यदि A, B को t सेकंड से हरा देता है, तो B हारने वाला और A जीतने वाला है। जब A फिनिश लाइन को पार करता है, तब B अभी भी A से पीछे है। इसलिए, B को बाकी रास्ता तय करने में t सेकंड लगते हैं। हम यह पता लगा सकते हैं कि हारने वाला (B) कितनी तेजी से चल रहा है।
• दौड़ के दौरान हमेशा धावकों के बीच एक निश्चित संबंध होता है, अर्थात्, वे हमेशा गति के अनुपात को बनाए रखते हैं।

उदाहरण: 200 मीटर की दौड़ में, A, S को 20 मीटर और N को 40 मीटर से हराता है। यदि S और N पहले की तरह ही गति से 100 मीटर की दौड़ रहे हैं, तो S, N को कितने मीटर से हराएगा? (क) 11.11 मीटर (ख) 10 मीटर (ग) 12 मीटर (घ) 25 मीटर

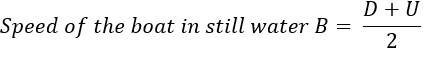
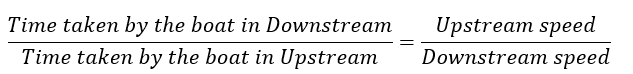
हल: विकल्प 'a' सही है। व्याख्या: जिस समय A को 200 मीटर दौड़ने में लगता है, S 180 मीटर दौड़ता है और N 160 मीटर दौड़ता है। इसलिए, जिस समय S को 200 मीटर दौड़ने में लगता है, N 200 (160/180) = 177.77 मीटर दौड़ता है या 22.22 मीटर पीछे रह जाता है। इसलिए, 100 मीटर में, N 11.11 मीटर पीछे रह जाता है।

4. वृत्ताकार गति

• जब वस्तुएँ विपरीत दिशाओं में चल रही होती हैं, तो उनकी सापेक्ष वेग उनके व्यक्तिगत वेगों के योग के बराबर होता है।
• जब दो वस्तुएँ समान दिशा में यात्रा कर रही होती हैं, तो उनके बीच की गति उनके पूर्ण गति के अंतर के बराबर होती है।

पहली मुलाकात

मान लें A और B दो धावक हैं।

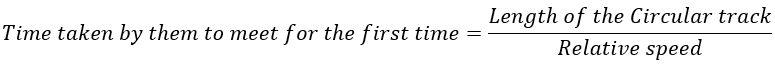
यदि A सबसे तेज धावक है और A B से t_AB घंटे बाद मिलता है, A C से t_AC घंटे बाद मिलता है, A D से t_AD सेकंड/घंटे बाद मिलता है, आदि, तो A ने सभी अन्य धावकों से पहली बार मुलाकात की है। A, B, C, D आदि के लिए पहली बार मिलने में लगने वाले समय का LCM t_AB है।

शुरुआती बिंदु पर पहली मुलाकात

मान लें कि धावक A सभी धावकों में सबसे तेज है और वह धावक B से पहली बार t_AB घंटों में, धावक C से पहली बार t_AC घंटों में, धावक D से पहली बार t_AD सेकंड/घंटों में, आदि में मिलता है। t_AB, t_AC, t_AD आदि का LCM वह समय है जब सभी एक साथ पहली बार मिलते हैं।

उदाहरण: आशिष और सागर एक वृत्ताकार ट्रैक पर विपरीत दिशाओं में क्रमशः 15 मीटर/सेकंड और 25 मीटर/सेकंड की गति से चल रहे हैं। ट्रैक की लंबाई 600 मीटर है। वे पहली बार कब मिलेंगे और वे पहली बार शुरुआती बिंदु पर कब मिलेंगे?

गति, समय और दूरी पर आधारित प्रश्नों को हल करने के लिए सुझाव और तरकीबें

छात्रों के लिए गति, समय और दूरी पर आधारित प्रश्नों को हल करने के लिए विभिन्न सुझाव और तरकीबें नीचे दी गई हैं।

• टिप 1: सापेक्ष गति को एक चलती हुई वस्तु की गति को दूसरी वस्तु के सापेक्ष परिभाषित किया जाता है। सापेक्ष गति के संभावित मामले हैं:
  • समान दिशा: जब दो वस्तुएं समान दिशा में चल रही होती हैं, तो सापेक्ष गति उनकी गति के बीच का अंतर होती है और इसे हमेशा एक सकारात्मक मान के रूप में व्यक्त किया जाता है।
  • विपरीत दिशा: जब दो वस्तुएं विपरीत दिशा में चल रही होती हैं, तो सापेक्ष गति उनकी गति का योग होती है।
• टिप 2: औसत गति = कुल दूरी / कुल समय
• टिप 3: जब एक ट्रेन एक चलती हुई व्यक्ति/बिंदु वस्तु को पार करती है, तो उस समय ट्रेन द्वारा तय की गई दूरी ट्रेन की लंबाई के बराबर होगी और सापेक्ष गति को निम्नलिखित रूप में लिया जाएगा:
  • यदि दोनों समान दिशा में चल रहे हैं, तो सापेक्ष गति = दोनों गति का अंतर।
  • यदि दोनों विपरीत दिशा में चल रहे हैं, तो सापेक्ष गति = दोनों गति का योग।
• टिप 4: लंबी वस्तु या प्लेटफार्म को पार करते समय: जब एक ट्रेन एक प्लेटफार्म या लंबी वस्तु को पार करती है, तो ट्रेन द्वारा उस वस्तु को पार करते समय तय की गई दूरी ट्रेन की लंबाई और उस वस्तु की लंबाई का योग होगी।
• टिप 5: एक व्यक्ति या बिंदु वस्तु को पार करते समय: जब एक ट्रेन एक व्यक्ति/वस्तु को पार करती है, तो ट्रेन द्वारा उस वस्तु को पार करते समय तय की गई दूरी ट्रेन की लंबाई के बराबर होगी।

गति, समय और दूरी के हल किए गए उदाहरण

उदाहरण 1: समय के लिए अनुपात = ⅕ : ¼ : ⅙ = 12 : 15 : 10

उदाहरण 2: एक ट्रक 1200 किमी की दूरी 40 घंटे में तय करता है। ट्रक की औसत गति क्या है?

हल: औसत गति = कुल दूरी तय की गई / कुल समय लिया ⇒ औसत गति = 1200/40 ∴ औसत गति = 30 किमी/घंटा

उदाहरण 3: एक व्यक्ति एक चलती हुई एस्केलेटर पर 60 सेकंड में ऊपर जा सकता है। यदि एस्केलेटर 2 कदम/सेकंड की गति से चल रहा है और व्यक्ति की गति 3 कदम/सेकंड है जब एस्केलेटर स्थिर है, तो व्यक्ति को ऊपर जाने में कितना समय लगेगा जब एस्केलेटर नहीं चल रहा है?

हल: मान लीजिए कदमों की संख्या 'N' है। ∴ ऊपर जाते समय व्यक्ति की प्रभावी गति = (3 - 2) = 1 कदम/सेकंड = N/1 = 60 ∴ N = 60 कदम। अब, जब एस्केलेटर नहीं चल रहा है, तब व्यक्ति को ऊपर जाने में लगने वाला समय = 60/3 = 20 सेकंड।

उदाहरण 4: राहुल 50 किमी/घंटा की गति से दिल्ली से पुणे जाता है और 75 किमी/घंटा की गति से वापस आता है। यात्रा की औसत गति ज्ञात करें।

हल: दूरी दोनों मामलों में समान है ⇒ आवश्यक औसत गति = (2 × 50 × 75)/(50 + 75) = 7500/125 = 60 किमी/घंटा

उदाहरण 5: यदि ट्रेन A 30 सेकंड में एक पोल को 60 किमी/घंटा की गति से पार करती है, तो ट्रेन A की लंबाई ज्ञात करें।

हल: दिए गए, ट्रेन की गति = 60 किमी/घंटा ⇒ गति = 60 × 5/18 मीटर/सेकंड = 50/3 मीटर/सेकंड। दिए गए, ट्रेन A द्वारा पोल को पार करने में लिया गया समय = 30 सेकंड। पोल को पार करने में जो दूरी तय की जाएगी, वह ट्रेन की लंबाई के बराबर होगी। ⇒ दूरी = गति × समय ⇒ दूरी = 50/3 × 30 = 500 मीटर

उदाहरण 6: एक 150 मीटर लंबी ट्रेन 15 सेकंड में 270 मीटर लंबे प्लेटफॉर्म को पार करती है। 186 मीटर के प्लेटफॉर्म को पार करने में कितना समय लगेगा?

हल: 270 मीटर लंबे प्लेटफॉर्म को पार करते समय, ट्रेन द्वारा तय की गई कुल दूरी = 150 + 270 = 420 मीटर। ट्रेन की गति = तय की गई कुल दूरी/ले लिया गया समय = 420/15 = 28 मीटर/सेकंड। 186 मीटर लंबे प्लेटफॉर्म को पार करते समय, ट्रेन द्वारा तय की गई कुल दूरी = 150 + 186 = 336 मीटर। ∴ ट्रेन द्वारा लिया गया समय = तय की गई दूरी/ट्रेन की गति = 336/28 = 12 सेकंड।

उदाहरण 7: दो ट्रेनें समान दिशा में क्रमशः 43 किमी/घंटा और 51 किमी/घंटा की गति से चल रही हैं। तेज ट्रेन द्वारा धीमी ट्रेन में बैठे व्यक्ति को पार करने में लिया गया समय 72 सेकंड है। तेज ट्रेन की लंबाई (मीटर में) क्या है?

हल: दिए गए: 2 ट्रेनों की गति = 43 किमी/घंटा और 51 किमी/घंटा। दोनों ट्रेनों की सापेक्ष गति = (51 – 43) किमी/घंटा = 8 किमी/घंटा। सापेक्ष गति मीटर/सेकंड में = 8 × (5/18) मीटर/सेकंड ⇒ 72 सेकंड में ट्रेन द्वारा तय की गई दूरी = 8 × (5/18) × 72 = 160। इसलिए, तेज ट्रेन की लंबाई = 160 मीटर।

उदाहरण 8: एक ट्रेन जिसकी लंबाई 100 मीटर है, 72 किमी/घंटा की गति से यात्रा कर रही है। यह दूसरी ट्रेन जो 200 मीटर लंबी है और 54 किमी/घंटा की गति से उसी दिशा में यात्रा कर रही है, को ओवरटेक करने में कितना समय लगेगा?

हल: सापेक्ष गति = 72 - 54 किमी/घंटा (क्योंकि दोनों एक ही दिशा में यात्रा कर रहे हैं) = 18 किमी/घंटा = 18 × 10/36 मीटर/सेकंड = 5 मीटर/सेकंड। इसके अलावा, ट्रेन द्वारा ओवरटेक करने के लिए तय की गई दूरी = 100 मीटर + 200 मीटर = 300 मीटर। इसलिए, समय लिया गया = दूरी/गति = 300/5 = 60 सेकंड।

उदाहरण 9: एक नाव 40 मिनट में 20 किमी की दूरी तय करती है। यदि धारा की गति 2.5 किमी/घंटा है, तो वापस लौटने में उसे कितना अधिक समय लगेगा?

हल: डाउनस्ट्रीम में समय लिया गया = 40 मिनट = 40/60 = 2/3 घंटा। डाउनस्ट्रीम गति = 20/(2/3) = 30 किमी/घंटा। जैसा कि हम जानते हैं, धारा की गति = 1/2 × (डाउनस्ट्रीम गति - अपस्ट्रीम गति) ⇒ अपस्ट्रीम गति = 30 - 2 × 2.5 = 30 - 5 = 25 किमी/घंटा। वापस लौटने में समय लिया गया = 20/25 = 0.8 घंटा = 0.8 × 60 = 48 मिनट। ∴ नाव को वापस लौटने में = 48 - 40 = 8 मिनट अधिक लगेगा।

उदाहरण 10: एक जहाज जो किनारे से 156 किमी दूर है, उसमें एक छेद हो जाता है जिससे 13/2 मिनट में 2.5 मीट्रिक टन पानी प्रवेश करता है। 68 मीट्रिक टन का एक मात्रा इसे डूबने के लिए पर्याप्त होगी, लेकिन पंप प्रति घंटे 15 मीट्रिक टन निकाल सकते हैं। औसत गति कितनी होनी चाहिए ताकि यह किनारे पर पहुंचने के लिए ठीक उसी समय डूबने लगे?

क. 18 किमी/घंटा

ख. 60 किमी/घंटा

ग. 15 किमी/घंटा

घ. 10 किमी/घंटा

व्याख्या: एक मिनट में, प्रवाहित होने वाली मात्रा = 15/39 मीट्रिक टन। एक मिनट में, निकाली जाने वाली मात्रा = 15/60 = 1/4 मीट्रिक टन। एक घंटे में प्रभावी भरण दर = (15/39 - 1/4) मीट्रिक टन = 21/56 मीट्रिक टन/मिनट। यह तब तक डूबने के लिए समय = (68 × 156)/21 = 505 मिनट। आवश्यक गति = (156/505) = 0.3 किमी/मिनट = 0.3 × 60 किमी/घंटा = 18 किमी/घंटा।

उदाहरण 11: मुझे एक निश्चित स्थान पर एक निश्चित समय पर होना है और अगर मैं 4 किमी/घंटा की गति से चलूं तो मुझे 40 मिनट देर होगी, और अगर मैं 5 किमी/घंटा की गति से चलूं तो 40 मिनट पहले पहुंचूंगा। मुझे अपने गंतव्य पर पहुंचने के लिए सामान्य समय क्या है? क. 7 घंटे ख. 14 घंटे ग. 6 घंटे घ. 3.5 घंटे

हल: विकल्प 'ग' सही है। व्याख्या: मान लीजिए कि t सामान्य समय है।: दूरी D = 4 x (t - 2/3) = 5 x (t - 2/3) को हल करने पर, हमें t = 6 घंटे मिलता है।

उदाहरण 12: एक रेलवे यात्री टेलीग्राफ के खंभों की गिनती करता है जैसे ही वह उन्हें पार करता है। यदि वे 50 मीटर की दूरी पर हैं और ट्रेन 48 किमी/घंटा की गति से चल रही है, तो वह प्रति मिनट कितने खंभे पार करेगा?

• क. 16
• ख. 20
• ग. 24

हल: विकल्प 'क' सही है। व्याख्या: 48 किमी/घंटा = 48 x 5/18 मीटर/सेकंड = (49 x 5 x 60)/18। खंभों की संख्या = 800/50 = 16।