Open App

RRB NTPC/ASM/CA/TA Exam > RRB NTPC/ASM/CA/TA Notes > Mathematics for RRB NTPC (Hindi) > महत्वपूर्ण नोट्स: एचसीएफ (HCF) और एलसीएम (LCM)

महत्वपूर्ण नोट्स: एचसीएफ (HCF) और एलसीएम (LCM) | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download

एचसीएफ और एलसीएम संख्या प्रणाली का एक और बहुत महत्वपूर्ण विषय है। यह अवधारणा केवल संख्या प्रणाली तक सीमित नहीं है, बल्कि यह गणित से संबंधित कुछ प्रश्नों को हल करने में भी सहायक है, जो प्रतियोगी परीक्षाओं के लिए एक बहुत महत्वपूर्ण विषय है।

सबसे बड़ा समापवर्तक (एच.सी.एफ.)

दो या दो से अधिक संख्याओं का एच.सी.एफ. सबसे बड़ा ऐसा संख्या है जो उन सभी को ठीक से विभाजित करता है।

एच.सी.एफ. को सबसे बड़ा सामान्य भाजक (जी.सी.डी) भी कहा जाता है।
प्रत्येक संख्या के कुछ भाजक होते हैं, लेकिन यदि दो या दो से अधिक संख्याएँ एक साथ ली जाएँ तो उनके पास एक या अधिक सामान्य भाजक हो सकते हैं। उन सामान्य भाजकों में से, सबसे बड़ा सामान्य भाजक या सबसे बड़ा समापवर्तक उन संख्याओं का होगा।
जी.सी.डी / एच.सी.एफ. खोजने के लिए: मान लीजिए दो संख्याएँ हैं, ई और आर।
प्रत्येक संख्या का अभाज्य गुणनखंड लिखें।
ई और आर की मानक रूपों में सभी सामान्य अभाज्य गुणकों को खोजें।
पिछले चरण के परिणामों का गुणनफल ई और आर का जी.सी.डी होगा।

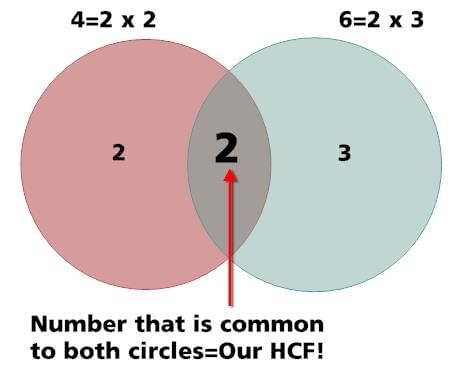
एचसीएफ 4 और 6 का चित्र नीचे दिखाया गया है:

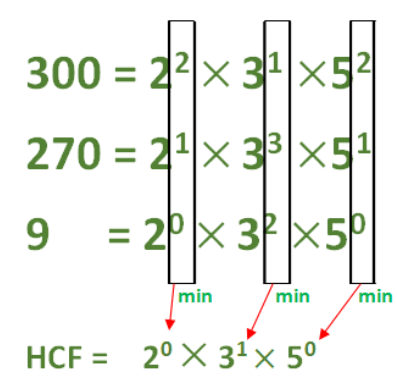
उदाहरण: 150, 210, 375 का जी.सी.डी निकालें।

हल:

चरण 1: संख्याओं का अभाज्य गुणनखंड लिखना ⇨ 150 = 5 X 5 X 3 X 2 ⇨ 210 = 5 X 2 X 7 X 3 ⇨ 375 = 5 X 5 X 5 X 3

चरण 2: तीनों संख्याओं में सामान्य अभाज्य गुणक लिखना है 5 X 3।

चरण 3: इसलिए, एच.सी.एफ. होगा 5 X 3 = 15।

महत्वपूर्ण नोट्स: एचसीएफ (HCF) और एलसीएम (LCM) | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

एच.सी.एफ. (Highest Common Factor) खोजने के तरीके

संख्याओं का एच.सी.एफ. खोजने के लिए मूलतः तीन तरीके हैं:

फैक्टराइजेशन विधि
डिवीजन विधि
प्राइम फैक्टराइजेशन

हम नीचे दिए गए तरीकों पर चर्चा करेंगे:

1. फैक्टराइजेशन विधि

प्रत्येक संख्या को उसके प्राइम कारकों के गुणन के रूप में व्यक्त करें और सामान्य कारकों की न्यूनतम शक्तियों के गुणन को एच.सी.एफ. प्राप्त करने के लिए लें।

हल करने के चरण:

चरण 1: प्रत्येक संख्या को उसके प्राइम कारकों के गुणन के रूप में लिखें। इसे यहां प्राइम फैक्टराइजेशन कहा जाता है।
चरण 2: अब दोनों संख्याओं के सामान्य कारकों को सूचीबद्ध करें।
चरण 3: सभी सामान्य प्राइम कारकों का गुणन एच.सी.एफ. है (प्रत्येक सामान्य कारक की निम्न शक्ति का उपयोग करें)।

उदाहरण: 60 और 75 का एच.सी.एफ. निकालें।

समाधान: प्रत्येक संख्या को उसके प्राइम कारकों के गुणन के रूप में लिखें। 22 x 3 x 5 = 60 और 3 x 52 = 75। सभी सामान्य प्राइम कारकों का गुणन एच.सी.एफ. है। इस उदाहरण में सामान्य प्राइम कारक 3 और 5 हैं। 3 की न्यूनतम शक्ति 1 है और 5 की 1 है। इसलिए, एच.सी.एफ. = 3 x 5 = 15।

2. डिवीजन विधि

चरण 1: छोटे संख्या को भाजक (divisor) और बड़ी संख्या को भागफल (dividend) के रूप में लें।
चरण 2: भाग करें। यदि शेषफल 0 है, तो भाजक दी गई संख्याओं का एच.सी.एफ. है।
चरण 3: यदि शेषफल 0 के अलावा है, तो शेषफल को नए भाजक के रूप में और पिछले भाजक को नए भागफल के रूप में लें।

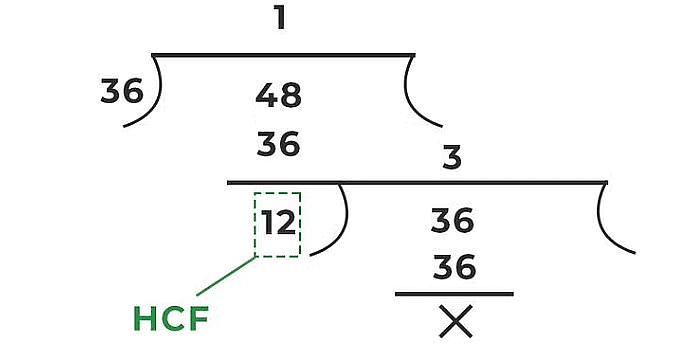
उदाहरण: 36 और 48 का एच.सी.एफ. निकालें।

समाधान:

चरण 1: हमें 48 को 36 से भाग देना है। अर्थात्, भागफल = 48 और भाजक = 36 [बड़ी संख्या को छोटी संख्या से भाग दें]।
चरण 2: दोनों संख्याओं का भाग दें।
चरण 3: जब 12 भाजक बनता है, तो शेषफल 0 हो जाता है। इसलिए, एच.सी.एफ. = 12। [अंतिम भाजक दी गई संख्याओं का आवश्यक एच.सी.एफ. है]।

3. प्रमुख गुणनखंड (फैक्टर ट्री) विधि

प्रमुख गुणनखंडन एक समग्र संख्या को उसके प्रमुख गुणनखंडों में तोड़ने की प्रक्रिया है, जो उन प्रमुख संख्याओं हैं जो मिलकर मूल संख्या देती हैं।

चरण 1: HCF की गणना करते समय, हम संख्याओं को प्रमुख संख्याओं में विभाजित करते हैं, जिन्हें प्रमुख गुणनखंड कहा जाता है।
चरण 2: दिए गए संख्याओं को 2 (पहली प्रमुख संख्या) से विभाजित करना शुरू करें, और तब तक विभाजित करते रहें जब तक संख्या को और नहीं तोड़ा जा सकता।
चरण 3: अंत में, संख्याओं को प्रमुख संख्याओं के उत्पाद के रूप में लिखें। इन सामान्य गुणनखंडों का उत्पाद दी गई संख्याओं का सबसे बड़ा समान गुणांक है।

उदाहरण: प्रमुख गुणनखंडन विधि का उपयोग करके 18 और 90 का HCF ज्ञात करें।

हल:

18 का प्रमुख गुणनखंडन नीचे दिया गया है:
90 का प्रमुख गुणनखंडन नीचे दिया गया है:
18 और 90 के 6 सामान्य गुणनखंड हैं, जो हैं 1, 2, 3, 6, 9, और 18। इसलिए, 18 और 90 का सबसे बड़ा समान गुणांक 18 है।

HCF ज्ञात करने की संक्षिप्त विधि

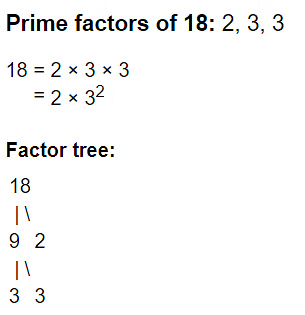
संख्याओं की पहचान करें: उन संख्याओं के सेट के साथ शुरुआत करें जिनके लिए आप HCF (Highest Common Factor) ढूंढना चाहते हैं।

अंतर की गणना करें: संख्याओं के जोड़ों के बीच के पूर्णांक का अंतर निकालें।
अंतर का HCF खोजें: प्राप्त हुए अंतर का HCF निकालें। यह मान मूल संख्याओं का भी HCF होगा।
मूल संख्याओं के साथ सत्यापित करें: वैकल्पिक रूप से, आप यह सत्यापित कर सकते हैं कि यह HCF मूल संख्याओं को बिना शेष छोड़ते विभाजित करता है।

उदाहरण: 36, 60, और 90 का HCF खोजें

समाधान:

चरण 1: संख्याओं की पहचान करें।

हम निम्नलिखित संख्याओं का HCF ढूंढना चाहते हैं: a = 36, b = 60, c = 90

चरण 2: अंतर की गणना करें।

अब, हम इन संख्याओं के जोड़ों के बीच के पूर्णांक का अंतर निकालेंगे:

60 और 36 के बीच का अंतर: |60 - 36| = 24
90 और 36 के बीच का अंतर: |90 - 36| = 54
90 और 60 के बीच का अंतर: |90 - 60| = 30

इस प्रकार हमारे द्वारा निकाले गए अंतर हैं: 24 (60 - 36 से), 54 (90 - 36 से), 30 (90 - 60 से)

चरण 3: अंतर का HCF खोजें।

अब हम निकाले गए अंतर का HCF निकालते हैं: 24, 54, और 30।

प्रत्येक अंतर के गुणांक:

24 के गुणांक: 1, 2, 3, 4, 6, 8, 12, 24
54 के गुणांक: 1, 2, 3, 6, 9, 18, 27, 54
30 के गुणांक: 1, 2, 3, 5, 6, 10, 15, 30

साझा गुणांक पहचानें:

24, 54, और 30 के सामान्य गुणांक: 1, 2, 3, 6

इसलिए, 24, 54, और 30 का HCF है 6.

न्यूनतम समापवर्तक (L.C.M.)

L.C.M का अर्थ है न्यूनतम या सबसे कम समापवर्तक। दो या अधिक संख्याओं का LCM वह सबसे छोटा सकारात्मक पूर्णांक है जो सभी दी गई संख्याओं द्वारा विभाजित किया जा सकता है।

दो संख्याओं E और R का LCM ज्ञात करना

संख्याओं E और R का प्राइम फैक्टराइजेशन ज्ञात करें।
उन सभी प्राइम फैक्टर को पता करें, जो किसी भी संख्या के मानक रूप में शामिल हैं।
उपरोक्त सूचीबद्ध प्रत्येक प्राइम फैक्टर को उस शक्ति तक बढ़ाएं जिसमें यह संख्याओं E और R के मानक रूप में प्रकट होता है।
पिछले चरण के परिणामों का गुणनफल E और R का LCM होगा।

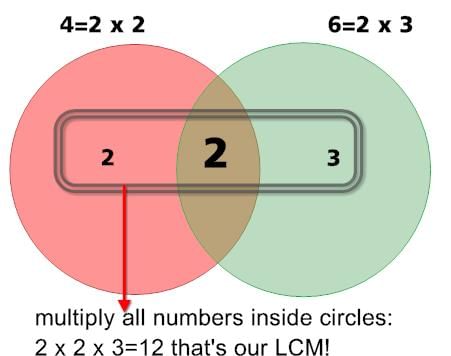
4 और 6 का LCM चित्र द्वारा नीचे दिखाया गया है:

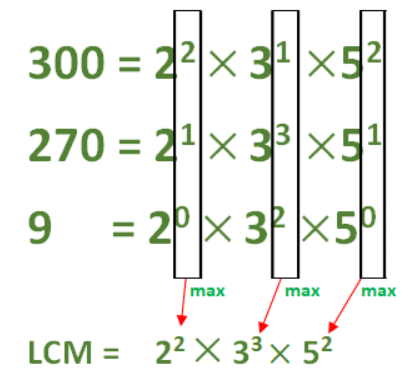
उदाहरण: 150, 210, 375 का LCM ज्ञात करें।

हल: चरण 1: संख्याओं का मानक रूप लिखना: ⇨ 150 = 5 × 5 × 3 × 2 = 5² × 3 × 2 ⇨ 210 = 5 × 2 × 7 × 3 ⇨ 375 = 5 × 5 × 5 × 3 = 5³ × 3

चरण 2: उन सभी प्राइम फैक्टर्स को लिखें: जो किसी भी संख्या में कम से कम एक बार प्रकट होते हैं: 5, 3, 2, 7।

चरण 3: प्रत्येक प्राइम फैक्टर को उनकी उच्चतम उपलब्ध शक्ति तक बढ़ाएं (संख्याओं पर विचार करते हुए)। LCM = 2 × 3 × 5 × 5 × 5 × 7 = 5250।

LCM ज्ञात करने के तरीके

1. प्राइम फैक्टराइजेशन विधि

शामिल चरण:

चरण 1: दिए गए संख्याओं के प्राइम फैक्टर्स को बार-बार विभाजन विधि द्वारा ज्ञात करें।
चरण 2: संख्याओं को उनके घातीय रूप में लिखें। केवल उन प्राइम फैक्टर्स का गुणनफल ज्ञात करें जिनकी उच्चतम शक्ति है।
चरण 3: इन उच्चतम शक्तियों वाले फैक्टर्स का गुणनफल दिए गए संख्याओं का LCM होगा।

उदाहरण: 60 और 90 का LCM प्राइम फैक्टराइजेशन का उपयोग करके ज्ञात करें।

हल: आइए हम प्राइम फैक्टराइजेशन विधि का उपयोग करके 60 और 90 का LCM ज्ञात करें।

चरण 1: 60 और 90 का प्राइम फैक्टराइजेशन इस प्रकार है: 60 = 2 × 2 × 3 × 5 और 90 = 2 × 3 × 3 × 5
चरण 2: यदि हम इन प्राइम फैक्टर्स को उनके घातीय रूप में लिखें तो यह इस प्रकार व्यक्त किया जाएगा, 60 = 2² × 3¹ × 5¹ और 90 = 2¹ × 3² × 5¹
चरण 3: अब, हम केवल उन फैक्टर्स का गुणनफल ज्ञात करेंगे जिनकी उच्चतम शक्तियाँ हैं। यह होगा, 2² × 3² × 5¹ = 4 × 9 × 5 = 180 => LCM(60,90) = 180

2. विभाजन विधि (शॉर्टकट विधि)

कदम 1: दिए गए संख्याओं को एक पंक्ति में व्यवस्थित करें।
कदम 2: एक संख्या से विभाजित करें जो ठीक से कम से कम दो दिए गए संख्याओं को विभाजित करती है और उन संख्याओं को आगे बढ़ाएं जो विभाज्य नहीं हैं।
कदम 3: उपरोक्त प्रक्रिया को दोहराएं जब तक कोई दो संख्याएँ एक ही संख्या से विभाजित नहीं होतीं, सिवाय 1 के।
कदम 4: विभाजकों और अविभाजित संख्याओं का गुणनफल दिए गए संख्याओं का आवश्यक L.C.M. है।

उदाहरण: 72, 240, 196 का L.C.M. ज्ञात करें।

हल: (i) प्रधान गुणनखंड विधि का उपयोग करते हुए:

⇨ 72 = 2 × 2 × 2 × 3 × 3 = 2³ × 3² ⇨ 240 = 2 × 2 × 2 × 2 × 3 × 5 = 2⁴ × 3 × 5 ⇨ 196 = 2 × 2 × 7 × 7 = 2² × 7²

दिए गए संख्याओं का L.C.M. = प्रत्येक दिए गए संख्या के सभी प्रधान गुणांक का गुणनफल, जिसमें सामान्य प्रधान गुणांक का सबसे बड़ा अनुक्रमांक है = 2⁴ × 3² × 5 × 7² = 16 × 9 × 5 × 49 = 35280।

(ii) विभाजन विधि का उपयोग करते हुए:

2 | 72, 240, 196

2 | 36, 120, 98

2 | 18, 60, 49

3 | 9, 30, 49

3 | 3, 10, 49

7 | 1, 10, 49

7 | 1, 10, 1

10 | 1, 10, 1

| 1, 1, 1

दिए गए संख्याओं का L.C.M. = विभाजकों और शेष संख्याओं का गुणनफल = 2 × 2 × 2 × 3 × 3 × 10 × 49 = 35280

को-प्राइम्स: दो संख्याओं को को-प्राइम्स कहा जाता है यदि उनका H.C.F. 1 है।

HCF और LCM के बीच संबंध

HCF और LCM के बीच संबंध

मान लें कि a और b दो संख्याएँ हैं, तो उनकी LCM और HCF के बीच संबंध को व्यक्त करने वाला सूत्र इस प्रकार है:

दो संख्याओं का गुणनफल = (दो संख्याओं का HCF) x (दो संख्याओं का LCM)
GCD (P, Q) × LCM (P, Q) = P × Q

नोट: यह नियम केवल दो संख्याओं के लिए लागू है।

दशमलव का H.C.F. और L.C.M. दिए गए संख्याओं में, कुछ संख्याओं में आवश्यकतानुसार शून्य जोड़कर समान दशमलव स्थान बनाएं। इन संख्याओं को बिना दशमलव बिंदु के विचार करते हुए, H.C.F. या L.C.M. की गणना करें। अब, परिणाम में, प्रत्येक दिए गए संख्या में जितने दशमलव स्थान हैं, उतने स्थान चिह्नित करें।

चरण I: प्रत्येक दशमलव को समान दशमलव में परिवर्तित करें।
चरण II: दशमलव बिंदु को हटा दें और सामान्य रूप से सबसे बड़ा सामान्य भाजक और न्यूनतम सामान्य गुणांक ज्ञात करें।
चरण III: उत्तर (सबसे बड़ा सामान्य भाजक / न्यूनतम सामान्य गुणांक) में, समान दशमलवों में जितने दशमलव स्थान हैं, उतना दशमलव बिंदु डालें।

उदाहरण: 3, 2.7, 0.09 का HCF और LCM ज्ञात करें।

हल: चरण-1: सभी संख्याओं को दशमलव बिंदु के बाद समान संख्या में अंकों के साथ लिखें। 3.00, 2.70, 0.09

चरण-2: अब दशमलव बिंदु के बाद अंकों की संख्या गिनें (उपरोक्त समस्या के लिए मान 2 है) और प्राप्त मान का 10 का घात निकालें। मान को n = 10² = 100 मानें। चरण-3: अब दशमलव बिंदु को हटा दें और संख्याओं का LCM और HCF ज्ञात करें। LCM(300, 270, 9) और HCF(300, 270, 9)।

300 = 2² x 3¹ x 5²
270 = 2¹ x 3³ x 5¹
9 = 2⁰ x 3² x 5⁰
LCM(300, 270, 9) = 2² x 3³ x 5² = 2700
HCF(300, 270, 9) = 2⁰ x 3¹ x 5⁰ = 3

LCM और HCF ज्ञात करने के लिए, हमें संख्याओं को ऊपर दिए गए अनुसार अभाज्य संख्याओं की शक्ति में लिखना चाहिए। हमें यह सुनिश्चित करना चाहिए कि सभी संख्याएँ समान संख्या की अभाज्य संख्याओं की शक्ति के रूप में लिखी जाएँ। उदाहरण: 9 को 3² के रूप में लिखा जा सकता है लेकिन अन्य दो संख्याएँ भी 2 और 5 को अभाज्य के रूप में शामिल करती हैं। इसलिए हम अन्य दो संख्याओं को 0 की शक्ति के रूप में लिख सकते हैं। इसलिए 9 को 2⁰ x 3² x 5⁰ के रूप में लिखा जा सकता है और इससे संख्या का मान नहीं बदलेगा। चूंकि हमारे पास संख्याएँ अभाज्य संख्याओं की शक्ति के रूप में हैं, अब LCM वह संख्या है जो अभाज्य संख्याओं के गुणनफल के रूप में बनती है, जिसमें समान अभाज्य में दी गई संख्याओं में शक्ति का अधिकतम मान होता है। LCM = 2 की शक्ति max(2, 1, 0) x 3 की शक्ति max(1, 3, 2) x 5 की शक्ति max(2, 1, 0) = 2² x 3³ x 5² = 2700। HCF की गणना समान है लेकिन केवल एक बदलाव के साथ। शक्ति में अधिकतम लेने के बजाय, हम न्यूनतम लेते हैं।

HCF = 2 की शक्ति min(2, 1, 0) x 3 की शक्ति min(1, 3, 2) x 5 की शक्ति min(2, 1, 0) = 2⁰ x 3¹ x 5⁰ = 3।

चरण-4: अब हमारे द्वारा प्राप्त उत्तर को चरण 2 में प्राप्त संख्या n से विभाजित करें। जो मान हम प्राप्त करते हैं वह हमारा आवश्यक उत्तर है।

LCM(3, 2.7, 9) = 2700/100 = 27

HCF(3, 2.7, 9) = 3/100 = 0.03

उदाहरण: 1.20 और 22.5 का H.C.F. और L.C.M. ज्ञात करें।

समाधान: निम्नलिखित दशमलव को समान दशमलव में परिवर्तित करने पर हमें मिलते हैं; 1.20 और 22.50

अब, प्रत्येक संख्या को दशमलव के बिना प्राइम के गुणनफल के रूप में व्यक्त करने पर हमें मिलता है

120 = 2 × 2 × 2 × 3 × 5 = 2³ × 3 × 5

2250 = 2 × 3 × 3 × 5 × 5 × 5 = 2 × 3² × 5³

अब, H.C.F. (उच्चतम समान भाजक) 120 और 2250 का = 2 × 3 × 5 = 30

इसलिए, H.C.F. 1.20 और 22.5 का = 0.30 (2 दशमलव स्थान लेते हुए)

L.C.M. (न्यूनतम समान गुणनफल) 120 और 2250 का = 2³ × 3² × 5³ = 9000

इसलिए, L.C.M. 1.20 और 22.5 का = 90.00 (2 दशमलव स्थान लेते हुए)

उदाहरण: 0.48, 0.72 और 0.108 का H.C.F. और L.C.M. ज्ञात करें

समाधान: निम्नलिखित दशमलव को समान दशमलव में परिवर्तित करने पर हमें मिलते हैं;

0.480, 0.720 और 0.108

480 = 2 × 2 × 2 × 2 × 2 × 3 × 5 = 2⁵ × 3 × 5

720 = 2 × 2 × 2 × 2 × 3 × 3 × 5 = 2⁴ × 3² × 5

108 = 2 × 2 × 3 × 3 × 3 = 2² × 3³

अब, H.C.F. 480, 720 और 108 का = 2² × 3 = 12

इसलिए, H.C.F. 0.48, 0.72 और 0.108 का = 0.012 (3 दशमलव स्थान लेते हुए)

L.C.M. 480, 720 और 108 का = 2⁵ × 3³ × 5 = 4320

इसलिए, L.C.M. 0.48, 0.72, 0.108 का = 4.32 (3 दशमलव स्थान लेते हुए)

भिन्नों का H.C.F. और L.C.M.

भिन्नों का H.C.F. (उच्चतम समान भाजक) और L.C.M. (न्यूनतम समान गुणनफल) ज्ञात करने के लिए, उनके अंश और हर को अलग-अलग H.C.F. और L.C.M. ज्ञात करें।

(क) HCF: भिन्नों का HCF ज्ञात करने के लिए, उनके अंश और हर का HCF व्यक्तिगत रूप से ज्ञात करें।

भिन्न 3/6 और 5/15 के लिए, अंश का HCF (3 और 5) 1 है, और हर का HCF (6 और 15) 3 है। इस प्रकार, भिन्नों का HCF 1/3 है।

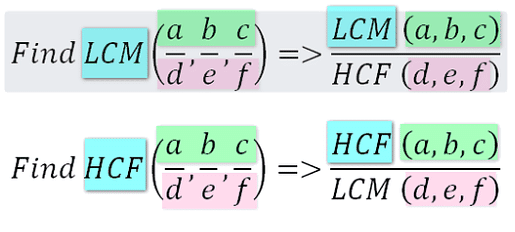
(b) LCM: भिन्नों का सबसे छोटा गुणनखंड (LCM) निकालने के लिए, उनके अंशों और हरों का LCM अलग-अलग निकालें।

अंशों का LCM (3 और 5) 15 है, और हरों का LCM (6 और 15) 30 है। इसलिए, भिन्नों का LCM 15/30 है, जो 1/2 में सरलित होता है।

गुणधर्मों की सूची

LCM और HCF का गुणा किसी भी दो दिए गए स्वाभाविक संख्याओं के लिए उन संख्याओं के गुणन के बराबर होता है। LCM × HCF = संख्याओं का गुणन। मान लीजिए A और B दो संख्याएँ हैं, तो LCM (A & B) × HCF (A & B) = A × B उदाहरण के लिए: यदि 3 और 8 दो संख्या हैं। LCM (3,8) = 24 HCF (3,8) = 1 LCM (3,8) × HCF (3,8) = 24 × 1 = 24 और, 3 × 8 = 24 इसलिए, सिद्ध हुआ।

गुणधर्म 1

किसी भी दो दिए गए स्वाभाविक संख्याओं के लिए LCM और HCF का गुणा उन संख्याओं के गुणन के बराबर होता है। LCM × HCF = संख्याओं का गुणन।

गुणधर्म 2

को-प्राइम संख्याओं का HCF 1 होता है। इसलिए, दिए गए को-प्राइम संख्याओं का LCM उन संख्याओं के गुणन के बराबर होता है। को-प्राइम संख्याओं का LCM = संख्याओं का गुणन उदाहरण के लिए: मान लीजिए हम दो को-प्राइम संख्याएँ लेते हैं, जैसे 21 और 22। 21 और 22 का LCM = 462 21 और 22 का गुणन = 462 LCM (21, 22) = 21 × 22
को-प्राइम संख्याओं का HCF 1 होता है।
इसलिए, दिए गए को-प्राइम संख्याओं का LCM उन संख्याओं के गुणन के बराबर होता है। को-प्राइम संख्याओं का LCM = संख्याओं का गुणन

गुणधर्म 3

H.C.F. और L.C.M. भिन्नों के लिए LCM का सूत्र है: भिन्नों का LCM = अंशों का LCM / हर का HCF। भिन्नों का HCF = अंशों का HCF / हर का LCM। उदाहरण के लिए: मान लीजिए हम दो भिन्नें 4/9 और 6/21 लेते हैं। 4 और 6 अंश हैं और 9 और 21 हर हैं। LCM (4, 6) = 12 HCF (4, 6) = 2 LCM (9, 21) = 63 HCF (9, 21) = 3 अब सूत्र के अनुसार, हम लिख सकते हैं: LCM (4/9, 6/21) = 12/3 = 4। फिर HCF (4/9, 6/21) = 2/63

H.C.F. और L.C.M. भिन्नों के लिए LCM का सूत्र है: भिन्नों का LCM = अंशों का LCM / हर का HCF। भिन्नों का HCF = अंशों का HCF / हर का LCM।

गुणधर्म 4

दो या अधिक संख्याओं का HCF कभी भी दिए गए संख्याओं में से किसी भी संख्या से बड़ा नहीं होता।

उदाहरण के लिए: 4 और 8 का HCF 4 है। यहाँ, एक संख्या 4 स्वयं है और दूसरी संख्या 8 HCF (4, 8) से बड़ी है, अर्थात् 4।

गुण 5

दो या अधिक संख्याओं का LCM कभी भी दिए गए संख्याओं में से किसी भी संख्या से छोटा नहीं होता।
उदाहरण के लिए: 4 और 8 का LCM 8 है जो कि इनमें से किसी भी संख्या से छोटा नहीं है।

HCF और LCM पर आधारित शेषफल संबंधी समस्याएँ

शेषफल खोजने पर परीक्षा में आमतौर पर चार प्रकार के प्रश्न होते हैं; इन प्रश्नों को हल करने के लिए HCF और LCM के सिद्धांतों की आवश्यकता होती है। आइए हम इन सूत्रों और उनके कार्य को उदाहरणों की मदद से समझते हैं, प्रत्येक प्रकार पर एक-एक उदाहरण के साथ।

सूत्र संख्या 1

सबसे बड़ा संख्या जो A, B, और C को विभाजित करती है, शेषफल p, q, और r छोड़ते हुए, वह (A-p), (B-q), और (C-r) का HCF है। आइए इसे निम्नलिखित उदाहरण से समझते हैं।
उदाहरण: वह सबसे बड़ा संख्या क्या है जो 77, 48, और 34 को विभाजित करती है, और क्रमशः शेषफल 2, 3, और 4 छोड़ती है? समाधान: सबसे बड़ा संख्या (77 – 2), (48 – 3), और (34 – 4) का HCF होगा = HCF (75, 45 और 30), जो कि 15 है।

सूत्र संख्या 2

सबसे छोटा संख्या जो A, B, और C से विभाज्य है, प्रत्येक मामले में समान शेष "r" छोड़ती है, वह (A, B, और C) का LCM r है। आइए इसे निम्नलिखित उदाहरण से समझते हैं।

उदाहरण: सबसे छोटा संख्या क्या है जो 48, 36, और 72 से विभाजित होने पर प्रत्येक मामले में 3 का शेष छोड़ती है? समाधान: सबसे छोटा संख्या होगा (48, 36, और 72) का LCM 3। LCM = 144। इसलिए, आवश्यक संख्या है 144 + 3 = 147।

सूत्र संख्या 3

सबसे बड़ा संख्या जो p, q, और r को विभाजित करेगी, प्रत्येक मामले में समान शेष छोड़ते हुए, तो आवश्यक संख्या = (p-q), (q-r), और (r-p) के पूर्णांक मानों का HCF है। आइए इसे निम्नलिखित उदाहरण से समझते हैं।
उदाहरण: सबसे बड़ा संख्या क्या है जो 65, 81, और 145 को विभाजित करती है, प्रत्येक मामले में समान शेष छोड़ते हुए? समाधान: आवश्यक संख्या = (81-65), (145-81), और (145-65) का HCF = (16, 64, और 80) का HCF = 16।

सूत्र संख्या 4

यदि हमें सबसे छोटा संख्या खोजना है जो a, b, और c से विभाजित होने पर क्रमशः समान शेष p, q, और r छोड़ती है, तो यदि यह देखा जाए कि (a-p) = (b-q) = (c-r) = k (मान लीजिए), तब आवश्यक संख्या = (a, b, और c का LCM) - k होगी। आइए इसे एक उदाहरण से समझते हैं।
उदाहरण: सबसे छोटा संख्या क्या है जो 6, 7 और 9 से विभाजित होने पर क्रमशः 1, 2 और 4 का शेष छोड़ती है? समाधान: यहाँ हम देखते हैं कि (6-1)=(7-2)=(9-4)=5। इसलिए, सूत्र लागू करके हमें आवश्यक संख्या मिलती है = (6, 7, और 9 का LCM) - 5 = 126 - 5 = 121।

HCF संख्याओं के रूप में (am-1) और (an-1)

प्रत्यक्ष सूत्र: HCF = aHCF(m,n) - 1

प्रश्न: 2120-1 और 250-1 का HCF ज्ञात करें। समाधान: (120, 50) का HCF = 10। सीधे सूत्र का प्रयोग करने पर, आवश्यक HCF = 210-1 प्राप्त होता है।

हल किए गए प्रश्न उदाहरण 1: कितने पूर्णांक (x, y) के जोड़े हैं जिनका गुणनफल x, y और HCF (x, y) = 1080 है? क. 8 ख. 7 ग. 9 घ. 12 उत्तर: विकल्प 'ग' सही है।

हल किए गए प्रश्न उदाहरण 1: कितने पूर्णांक (x, y) के जोड़े हैं जिनका गुणनफल x, y और HCF (x, y) = 1080 है? क. 8 ख. 7 ग. 9 घ. 12 उत्तर: विकल्प 'ग' सही है।

समाधान: हमें क्रमबद्ध जोड़े (x, y) ज्ञात करने हैं ताकि xy * HCF(x, y) = 1080। मान लेते हैं x = ha और y = hb जहाँ h = HCF(x, y) => HCF(a, b) = 1। तो h³(ab) = 1080 = (2³)(3³)(5)। हमें 1080 को एक पूर्ण घन और एक अन्य संख्या के गुणनफल के रूप में लिखना है। चार मामले:

1. h = 1, ab = 1080 और b सह-प्राइम हैं। हमें 4 जोड़े मिले, 8 क्रमबद्ध जोड़े (1, 1080), (8, 135), (27, 40) और (5, 216)। (वास्तव में हम सह-प्राइम a,b ढूंढ रहे हैं ताकि a*b = 1080)।
2. h = 2, हमें (3³) * (5) को दो सह-प्राइम संख्याओं के गुणनफल के रूप में लिखने के तरीके ज्ञात करने हैं। यह दो तरीकों से किया जा सकता है - 1 और (3³) * (5), (3³) और (5) के लिए जोड़ों की संख्या = 2, क्रमबद्ध जोड़ों की संख्या = 4।
3. h = 3, जोड़ों की संख्या = 2, क्रमबद्ध जोड़ों की संख्या = 4।
4. h = 6, जोड़ों की संख्या = 1, क्रमबद्ध जोड़ों की संख्या = 2।

इसलिए (x, y) के कुल जोड़े = 9, क्रमबद्ध जोड़ों की कुल संख्या = 18। जोड़े हैं (1, 1080), (8, 135), (27, 40), (5, 216), (2, 270), (10, 54), (3, 120), (24, 15) और (6, 30)।

अतः उत्तर है "9"

उदाहरण 2: सबसे छोटा संख्या ज्ञात करें जो 5 से विभाजन पर 4, 6 से विभाजन पर 5, 7 से विभाजन पर 6, 8 से विभाजन पर 7, और 9 से विभाजन पर 8 शेष छोड़ता है। क. 2519 ख. 5039 ग. 1079 घ. 979 उत्तर: विकल्प 'क' सही है।

हल: जब किसी संख्या को 8 से विभाजित किया जाता है, तो शेषफल 7 को -1 के रूप में समझा जा सकता है। यह विचार कई प्रश्नों में बहुत उपयोगी है। इसलिए, N = 5a - 1 या N 1 = 5a, N = 6b - 1 या N 1 = 6b, N = 7c - 1 या N 1 = 7c, N = 8d - 1 या N 1 = 8d, N = 9e - 1 या N 1 = 9e। N 1 को (5, 6, 7, 8, 9) के गुणज के रूप में व्यक्त किया जा सकता है। N 1 = 5a x 6b x 7c x 8d x 9e या N = (5a x 6b x 7c x 8d x 9e) - 1। N का सबसे छोटा मान तब होगा जब हम (5, 6, 7, 8, 9) का सबसे छोटा सामान्य गुणांक या LCM निकालेंगे। N = LCM (5, 6, 7, 8, 9) - 1 = 2520 - 1 = 2519। इसलिए उत्तर है "2519"।

उदाहरण 3: छह घड़ियाँ एक साथ बजना शुरू करती हैं और क्रमशः 2, 4, 6, 8, 10 और 12 सेकंड के अंतराल पर बजती हैं। 30 मिनट में, वे कितनी बार एक साथ बजती हैं?

हल: इस प्रश्न में, हमें वह सबसे छोटा संख्या ढूंढनी है जो 2, 4, 6, 8, 10 और 12 से विभाज्य हो। और वह संख्या दिए गए छह संख्याओं का LCM होना चाहिए। LCM (2, 4, 6, 8, 10, 12) = 120। इसका मतलब है कि पहली बार सभी छह घड़ियाँ एक साथ 120 सेकंड या 2 मिनट पर बजेंगी। इसलिए, 30 मिनट में वे बजेंगी = 30/2 = 15 बार।

उदाहरण 4: दो घड़ियाँ हैं, एक 5 मिनट में 96 बार बजती है और दूसरी 7 मिनट में 48 बार बजती है। यदि वे 10 बजे एक साथ बजती हैं, तो वे अगली बार कब एक साथ बजेंगी?

हल: प्रत्येक बीट का समय 5/96 मिनट और 7/48 मिनट है, या 5/96 मिनट और 14/96 मिनट। अंशों का LCM = 70 और हर का HCF = 90। इसलिए, अंश का LCM =

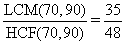
उदाहरण 5: राकेश और बृजेेश अकेले क्रमशः 12 दिन और 15 दिन में काम कर सकते हैं। यदि वे एक साथ काम करें तो वे काम कितने दिन में पूरा करेंगे?

हल: मान लेते हैं कि कार्य = LCM (12, 15) = 60 इकाइयाँ। राकेश द्वारा एक दिन में किए गए कार्य की इकाइयाँ = 60/12 = 5 इकाइयाँ। इसी प्रकार, ब्रिजेश द्वारा एक दिन में किए गए कार्य की इकाइयाँ = 60/15 = 4 इकाइयाँ। इसलिए, एक दिन में वे मिलकर 5 + 4 = 9 इकाइयाँ कार्य पूरा कर सकते हैं। अतः, कार्य पूरा करने में कुल समय = 60/9 = 20/3 दिन।

उदाहरण 6: सरिता और नमिता एक ही बिंदु से 120 मीटर लंबाई के वृत्ताकार ट्रैक पर क्रमशः 10 मीटर/सेकंड और 16 मीटर/सेकंड की गति से समानांतर दौड़ना शुरू करती हैं। वे फिर से प्रारंभिक बिंदु पर कितने समय में मिलेंगी?

हल: सरिता द्वारा एक चक्कर पूरा करने में लिया गया समय = 120/10 = 12 सेकंड। इसी प्रकार, नमिता द्वारा एक चक्कर पूरा करने में लिया गया समय = 120/16 = 15/2 सेकंड। इसलिए, समय जिसके बाद दोनों फिर से प्रारंभिक बिंदु पर होंगी = LCM (12, 15/2) = 60 सेकंड = 1 मिनट।

The document महत्वपूर्ण नोट्स: एचसीएफ (HCF) और एलसीएम (LCM) | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA is a part of the RRB NTPC/ASM/CA/TA Course Mathematics for RRB NTPC (Hindi).

All you need of RRB NTPC/ASM/CA/TA at this link: RRB NTPC/ASM/CA/TA

	Mathematics for RRB NTPC (Hindi) 142 videos\|172 docs\|185 tests

Mathematics for RRB NTPC (Hindi)

142 videos|172 docs|185 tests

Join Course for Free

About this Document

4.83/5 Rating

Oct 18, 2025 Last updated

Related Exams

RRB NTPC/ASM/CA/TA Bank Exams SSC JE SSC CGL

Document Description: महत्वपूर्ण नोट्स: एचसीएफ (HCF) और एलसीएम (LCM) for RRB NTPC/ASM/CA/TA 2025 is part of Mathematics for RRB NTPC (Hindi) preparation. The notes and questions for महत्वपूर्ण नोट्स: एचसीएफ (HCF) और एलसीएम (LCM) have been prepared according to the RRB NTPC/ASM/CA/TA exam syllabus. Information about महत्वपूर्ण नोट्स: एचसीएफ (HCF) और एलसीएम (LCM) covers topics like HCF और LCM के बीच संबंध, हल किए गए प्रश्न उदाहरण 1: कितने पूर्णांक (x, y) के जोड़े हैं जिनका गुणनफल x, y और HCF (x, y) = 1080 है? क. 8 ख. 7 ग. 9 घ. 12 उत्तर: विकल्प 'ग' सही है। and महत्वपूर्ण नोट्स: एचसीएफ (HCF) और एलसीएम (LCM) Example, for RRB NTPC/ASM/CA/TA 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for महत्वपूर्ण नोट्स: एचसीएफ (HCF) और एलसीएम (LCM).

Introduction of महत्वपूर्ण नोट्स: एचसीएफ (HCF) और एलसीएम (LCM) in English is available as part of our Mathematics for RRB NTPC (Hindi) for RRB NTPC/ASM/CA/TA & महत्वपूर्ण नोट्स: एचसीएफ (HCF) और एलसीएम (LCM) in Hindi for Mathematics for RRB NTPC (Hindi) course. Download more important topics related with notes, lectures and mock test series for RRB NTPC/ASM/CA/TA Exam by signing up for free. RRB NTPC/ASM/CA/TA: महत्वपूर्ण नोट्स: एचसीएफ (HCF) और एलसीएम (LCM) | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

Description

Full syllabus notes, lecture & questions for महत्वपूर्ण नोट्स: एचसीएफ (HCF) और एलसीएम (LCM) | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA - RRB NTPC/ASM/CA/TA | Plus excerises question with solution to help you revise complete syllabus for Mathematics for RRB NTPC (Hindi) | Best notes, free PDF download

Information about महत्वपूर्ण नोट्स: एचसीएफ (HCF) और एलसीएम (LCM)

In this doc you can find the meaning of महत्वपूर्ण नोट्स: एचसीएफ (HCF) और एलसीएम (LCM) defined & explained in the simplest way possible. Besides explaining types of महत्वपूर्ण नोट्स: एचसीएफ (HCF) और एलसीएम (LCM) theory, EduRev gives you an ample number of questions to practice महत्वपूर्ण नोट्स: एचसीएफ (HCF) और एलसीएम (LCM) tests, examples and also practice RRB NTPC/ASM/CA/TA tests

	Mathematics for RRB NTPC (Hindi) 142 videos\|172 docs\|185 tests

Mathematics for RRB NTPC (Hindi)

142 videos|172 docs|185 tests

Join Course for Free

Download as PDF

Explore Courses for RRB NTPC/ASM/CA/TA exam

Viva Questions

MCQs

Objective type Questions

ppt

past year papers

Free

study material

Exam

video lectures

Important questions

Sample Paper

practice quizzes

mock tests for examination

shortcuts and tricks

Semester Notes

Extra Questions

Summary

pdf

महत्वपूर्ण नोट्स: एचसीएफ (HCF) और एलसीएम (LCM) | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

Previous Year Questions with Solutions

महत्वपूर्ण नोट्स: एचसीएफ (HCF) और एलसीएम (LCM) | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

;

Additional Information about महत्वपूर्ण नोट्स: एचसीएफ (HCF) और एलसीएम (LCM) for RRB NTPC/ASM/CA/TA Preparation

महत्वपूर्ण नोट्स: एचसीएफ (HCF) और एलसीएम (LCM) Free PDF Download

The महत्वपूर्ण नोट्स: एचसीएफ (HCF) और एलसीएम (LCM) is an invaluable resource that delves deep into the core of the RRB NTPC/ASM/CA/TA exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the महत्वपूर्ण नोट्स: एचसीएफ (HCF) और एलसीएम (LCM) now and kickstart your journey towards success in the RRB NTPC/ASM/CA/TA exam.

Importance of महत्वपूर्ण नोट्स: एचसीएफ (HCF) और एलसीएम (LCM)

The importance of महत्वपूर्ण नोट्स: एचसीएफ (HCF) और एलसीएम (LCM) cannot be overstated, especially for RRB NTPC/ASM/CA/TA aspirants. This document holds the key to success in the RRB NTPC/ASM/CA/TA exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

महत्वपूर्ण नोट्स: एचसीएफ (HCF) और एलसीएम (LCM) Notes

महत्वपूर्ण नोट्स: एचसीएफ (HCF) और एलसीएम (LCM) Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to महत्वपूर्ण नोट्स: एचसीएफ (HCF) और एलसीएम (LCM). It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, महत्वपूर्ण नोट्स: एचसीएफ (HCF) और एलसीएम (LCM) Notes on EduRev are your ultimate resource for success.

महत्वपूर्ण नोट्स: एचसीएफ (HCF) और एलसीएम (LCM) RRB NTPC/ASM/CA/TA Questions

The "महत्वपूर्ण नोट्स: एचसीएफ (HCF) और एलसीएम (LCM) RRB NTPC/ASM/CA/TA Questions" guide is a valuable resource for all aspiring students preparing for the RRB NTPC/ASM/CA/TA exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study महत्वपूर्ण नोट्स: एचसीएफ (HCF) और एलसीएम (LCM) on the App

Students of RRB NTPC/ASM/CA/TA can study महत्वपूर्ण नोट्स: एचसीएफ (HCF) और एलसीएम (LCM) alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the महत्वपूर्ण नोट्स: एचसीएफ (HCF) और एलसीएम (LCM), students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of महत्वपूर्ण नोट्स: एचसीएफ (HCF) और एलसीएम (LCM) is prepared as per the latest RRB NTPC/ASM/CA/TA syllabus.

Education Revolution