महत्वपूर्ण अवधारणाएँ: मिश्रण और अनुपात (Alligations) | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download
अर्थ: मिश्रण और अनुपात
अर्थ: मिश्रण और अनुपात
- किसी चीज़ को एक साथ मिलाने को मिश्रण कहा जाता है।
- अनुपात हमें यह पता लगाने में मदद करता है कि कितनी मात्रा में प्रत्येक चीज़ मिलाई गई है और वे किस कीमत पर बेची जाती हैं ताकि लाभ या हानि हो सके।
- किसी चीज़ को एक साथ मिलाने को मिश्रण कहा जाता है।
- मिश्रण और अनुपात की समस्याओं को हल करने के लिए, आपको समझना होगा कि अनुपात यह पता लगाने में मदद करता है कि जब मिश्रित सामग्री के अनुपात और मात्रा भिन्न होते हैं, तब मिश्रण का औसत मूल्य क्या है। यह यह भी समझने में मदद करता है कि तत्वों को किस अनुपात में मिलाया गया है।
मिश्रण के प्रकार
- सरल मिश्रण: जब दो या अधिक विभिन्न सामग्रियों को मिलाया जाता है, तो एक सरल मिश्रण बनता है। सरल मिश्रणों पर आधारित समस्याएँ काफी सीधी और हल करने में आसान होती हैं। उदाहरण के लिए, धातुओं का मिश्रण, जिसे मिश्र धातु कहते हैं, सरल मिश्रण हैं।
- संयुक्त मिश्रण: जब दो या अधिक सरल मिश्रणों को मिलाया जाता है, तो एक संयुक्त मिश्रण बनता है। इसलिए, जटिल मिश्रणों की समस्याओं को हल करते समय अधिक अनुपात की गणना की आवश्यकता होती है। उदाहरण के लिए, जब विभिन्न तत्वों के संयोजन से बने दो धातु मिश्र धातुओं को मिलाया जाता है, तो यह एक जटिल मिश्रण बनाता है।
अनुपात का नियम


यह नियम हमें यह पता लगाने में मदद करता है कि दो या अधिक अवयवों/विभिन्न कीमतों/संकेन्द्रणों के मिश्रण को अंतिम मिश्रण या इच्छित कीमत या संकेन्द्रण बनाने के लिए किस अनुपात में मिलाया जाता है। दो विधियों का उपयोग किया जाता है:
विधि 1 (सूत्र विधि): इसे इस प्रकार दिया गया है-
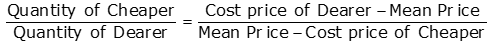
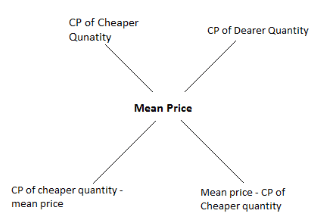
विधि 2 (चित्र विधि): उपरोक्त विधि को एक चित्र के माध्यम से व्यक्त किया जा सकता है जो समझने के लिए अधिक सुविधाजनक होगा-
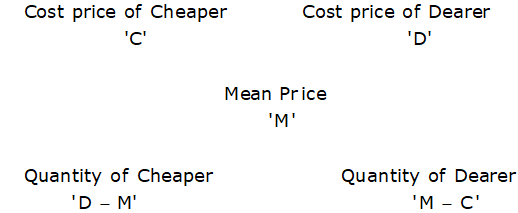
नोट: यह आरोप का नियम अन्य विषयों पर भी लागू किया जा सकता है जैसे लाभ और हानि, औसत, प्रतिशत, साधारण ब्याज/संयुक्त ब्याज, अनुपात, और अनुपात।
उदाहरण: 30 लड़कों का औसत वजन 60 किलोग्राम है और 20 लड़कियों का औसत वजन 40 किलोग्राम है। पूरे वर्ग का औसत वजन क्या है? समाधान: उपरोक्त प्रश्न का उत्तर पाने के लिए, हम भारित औसत का सूत्र उपयोग कर सकते हैं। मान लीजिये कि प्रश्न को थोड़ा अलग तरीके से तैयार किया गया था, लड़कों का औसत वजन 60, लड़कियों का औसत वजन 40 और पूरे वर्ग का औसत वजन 52 है।
लड़कों और लड़कियों की संख्या के बीच का अनुपात ज्ञात करें। समाधान: इस प्रश्न को हल करने का सबसे तेज़ तरीका आरोप का उपयोग करना होगा। नीचे आरोप का उपयोग कर इसके समाधान को पढ़ें।
आरोप वास्तव में क्या है?
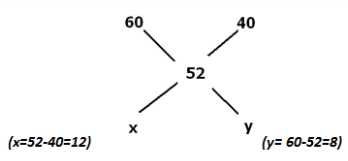
यह भारित औसत का उल्टा है; अर्थात्, यदि दो समूहों के औसत अलग से दिए गए हैं और पूरे समूह का औसत दिया गया है, तो हम समूहों के बीच अनुपात पता कर सकते हैं। उदाहरण के लिए, उपरोक्त प्रश्न में दिए गए डेटा हैं- लड़कों का औसत वजन = 60, लड़कियों का औसत वजन = 40 और पूरे वर्ग का औसत वजन = 52। डेटा को निम्नलिखित आरोप चार्ट में प्रदर्शित किया जा सकता है और इसका उपयोग करके हम कक्षा में लड़कों और लड़कियों की संख्या के बीच अनुपात ज्ञात कर सकते हैं।
अंतर को लें: x = 60-52 = 8 और y = 52-40 = 12। इस प्रकार हम लड़कों और लड़कियों के बीच अनुपात 12:8 या 3:2 प्राप्त करते हैं।
आइए एक और प्रश्न पर विचार करें जहाँ आप आरोप का उपयोग कर सकते हैं।
उदाहरण: एक दुकानदार को दो प्रकार की चावल को किस अनुपात में मिलाना चाहिए, एक की कीमत 20 रुपये/किलोग्राम और दूसरे की कीमत 10 रुपये/किलोग्राम है, ताकि उसे 14 रुपये/किलोग्राम की चावल की किस्म प्राप्त हो सके?
समाधान: यहाँ भी हम आरोप का उपयोग कर सकते हैं: x = 14-10 = 4 और y = 20-14 = 6। प्रकार 1 और प्रकार 2 चावल के बीच अनुपात 4:6 या 2:3 है।
महत्वपूर्ण सूत्र: गणित की समस्याओं को हल करने के लिए, आपको प्रत्येक विषय के लिए विशिष्ट सूत्र सीखने चाहिए। ये सूत्र प्रश्नों को जल्दी और आसानी से हल करने में मदद करते हैं। यहाँ कुछ सूत्र दिए गए हैं जो आपको मिश्रण और आरोप की समस्याओं को अधिक आसानी से हल करने में मदद करेंगे।
आवश्यक अनुपात ज्ञात करने के लिए जो अवयवों का मिश्रण होता है, उपयोग किया जाने वाला मूल सूत्र है: इसे आरोप का नियम भी कहा जाता है और इसे निम्नलिखित रूप में भी दर्शाया जा सकता है।
मिश्रण समस्याओं में आरोप का अनुप्रयोग
हम देखेंगे कि आरोप के नियम को मिश्रण की समस्याओं में कैसे लागू किया जा सकता है-
उदाहरण 1: एक दुकानदार 30 किलोग्राम प्रकार A चावल (40 रुपये/किलोग्राम) और 45 किलोग्राम प्रकार B चावल (30 रुपये/किलोग्राम) मिलाता है, तो चावल के बने मिश्रण की कीमत ज्ञात करें।
समाधान: आरोप के नियम के द्वारा: (30 – M): (M – 40) = 30: 45 = 2: 3
90 – 3M = 2M – 80
5M = 170
M = 34
इसलिए, मिश्रण की कीमत = 34 रुपये/किलोग्राम है।
नोट: मिश्रण की वस्तु की कीमत पर आरोप की अवधारणा लागू करने के बाद हमें पता चलेगा कि इन दो वस्तुओं या मिश्रण के बीच अनुपात क्या है।
उदाहरण 2: मिश्रण A (दूध और पानी) में 75% दूध है और मिश्रण B (दूध और पानी) में 10% पानी है, तो ज्ञात करें कि इन दोनों मिश्रणों को किस अनुपात में मिलाया जाए ताकि तीसरा मिश्रण 15% पानी वाला हो।
समाधान: मिश्रण A में पानी का प्रतिशत = 100% – 75% = 25%
आरोप के नियम द्वारा: आवश्यक अनुपात = -5: -10 = 1: 2
लाभ और हानि की समस्याओं में आरोप
यह दो वस्तुओं की लागत मूल्य और वस्तुओं पर लाभ/हानि प्रतिशत दिए जाने पर कुल लाभ या हानि प्रतिशत ज्ञात करने के लिए उपयोग किया जाता है।
उदाहरण 3: एक दुकानदार प्रकार A चावल को 20% लाभ पर और प्रकार B चावल को 15% हानि पर बेचता है। यदि कुल मिलाकर उसे 13% लाभ होता है, तो प्रकार A चावल की लागत मूल्य से प्रकार B चावल की लागत मूल्य ज्ञात करें।
समाधान: आरोप के नियम द्वारा: प्रकार A से प्रकार B चावल की लागत मूल्य का अनुपात = -28: -7 = 4: 1
नोट: वस्तुओं पर अर्जित लाभ/हानि प्रतिशत पर आरोप की अवधारणा लागू करने के बाद हमें वस्तुओं की लागत मूल्यों का अनुपात प्राप्त होगा।
उदाहरण 4: एक दुकानदार ने एक मेज 1200 रुपये में खरीदी और 20% लाभ पर बेची, उसने एक कुर्सी 400 रुपये में खरीदी और 10% लाभ पर बेची, तो उसका कुल लाभ प्रतिशत ज्ञात करें।
समाधान: मान लें कि कुल लाभ प्रतिशत = M%
आरोप के नियम द्वारा: (10 – M): (M – 20) = 1200: 400 = 3: 1
10 – M = 3M – 60
4M = 70
M = 17.5
इसलिए, कुल लाभ प्रतिशत = M = 17.5% है।
गति, दूरी, और समय की समस्याओं में आरोप
मिश्रण और आरोप की अवधारणा का उपयोग यात्रा की औसत गति ज्ञात करने के लिए किया जा सकता है।
उदाहरण 5: एक व्यक्ति यात्रा के पहले 3 घंटे 80 किमी/घंटा की गति से और शेष 5 घंटे 56 किमी/घंटा की गति से यात्रा करता है, तो उसकी यात्रा की औसत गति ज्ञात करें।
समाधान: मान लें कि औसत गति = X
आरोप के नियम द्वारा: (56 – X): (X – 80) = 3: 5
280 – 5X = 3X – 240
8X = 520
X = 65
यात्रा की औसत गति = 65 किमी/घंटा है।
नोट: यात्रा के विभिन्न हिस्सों पर गति के आरोप की अवधारणा लागू करने के बाद हमें उन हिस्सों को कवर करने के लिए समय का अनुपात प्राप्त होगा।
उदाहरण 6: 360 किमी की दूरी 6 घंटे में तय की जा सकती है जब यात्रा के कुछ हिस्से को 45 किमी/घंटा की गति से और शेष को 90 किमी/घंटा की गति से तय किया जाता है, तो 45 किमी/घंटा की गति से तय की गई दूरी ज्ञात करें।
समाधान: यात्रा की औसत गति = 360/6 = 60 किमी/घंटा
आरोप के नियम द्वारा: समय का अनुपात = 30: 15 = 2: 1
45 किमी/घंटा की गति से यात्रा का समय = 6 * (2/3) = 4 घंटे
45 किमी/घंटा की गति से तय की गई दूरी = 45 * 4 = 180 किमी।
साधारण/संयुक्त ब्याज की समस्याओं में आरोप
यदि हम दिए गए समय अवधि के लिए प्रभावशाली ब्याज दर की गणना कर सकते हैं, तो हम साधारण ब्याज (SI) और संयुक्त ब्याज (CI) में आरोप को लागू कर सकते हैं।
उदाहरण 7: राहुल ने सुमित को 25% SI पर 2 वर्षों के लिए 5000 रुपये उधार दिए और सुरेश से 3 वर्षों के लिए 10% SI पर 3000 रुपये उधार लिए, फिर राहुल के ब्याज राशि पर लाभ/हानि ज्ञात करें।
समाधान: उधार दी गई राशि पर 2 वर्षों के लिए प्रभावशाली ब्याज की दर = 25% * 2 = 50%
उधार ली गई राशि पर 3 वर्षों के लिए प्रभावशाली ब्याज की दर = -10% * 3 = -30% [नकारात्मक क्योंकि ब्याज का भुगतान किया जाएगा।]
आरोप के नियम द्वारा: (-30 – X): (X – 50) = 5000: 3000 = 5: 3
-90 – 3X = 5X – 250
8X = 160
X = 20
इसलिए, ब्याज राशि पर कुल लाभ = 20% (5000 - 3000) = 1600 रुपये है।
नोट: प्रभावशाली ब्याज दर पर आरोप की अवधारणा लागू करने के बाद हमें निवेश की गई राशि का अनुपात प्राप्त होगा।
औसत, अनुपात, और प्रतिशत की समस्याओं में आरोप
आरोप के नियम को लागू करके हम औसत, अनुपात, और प्रतिशत की समस्याओं को जल्दी हल कर सकते हैं।
उदाहरण 8: एक कक्षा के 25 छात्रों की औसत उम्र 24 वर्ष है और कक्षा के शेष 15 छात्रों की औसत उम्र 18 वर्ष है, तो कक्षा की औसत उम्र ज्ञात करें।
समाधान: मान लें कि कक्षा की औसत उम्र = A
आरोप के नियम द्वारा: (18 – A): (A – 24) = 25: 15 = 5: 3
54 – 3A = 5A – 120
8A = 174
A = 21.75
इसलिए, कक्षा की औसत उम्र = A = 21.75 वर्ष है।
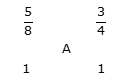
उदाहरण 9: अरुण द्वारा गणित और अंग्रेजी में प्राप्त अंक और अधिकतम अंक का अनुपात 5: 3 और 3: 1 है। यदि दोनों विषयों में अधिकतम अंक समान हैं, तो जब दोनों विषयों को एक साथ लिया जाता है, तो अरुण द्वारा प्राप्त अंक और अधिकतम अंक का अनुपात ज्ञात करें।
समाधान: आरोप के नियम द्वारा: (3/4 – A): (A – 5/8) = 1: 1
3/4 – A = A – 5/8
2A = 11/8
A = 11/16
आवश्यक अनुपात = 11: (16 – 11) = 11: 5।
उदाहरण 10: राज्यों A और B की कुल जनसंख्या में, पुरुष जनसंख्या क्रमशः 60% और 50% है। यदि दोनों राज्यों को एक साथ लिया जाए तो पुरुष जनसंख्या कुल जनसंख्या का 58% बन जाती है, तो ज्ञात करें कि राज्य B की कुल जनसंख्या राज्य A की कुल जनसंख्या का कितना प्रतिशत है।
समाधान: आरोप के नियम द्वारा: राज्य A की कुल जनसंख्या और राज्य B की कुल जनसंख्या का अनुपात = -8: -2 = 4: 1
आवश्यक प्रतिशत = (1/4) * 100 = 25%
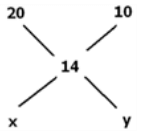
उदाहरण: एक दुकानदार को दो प्रकार की चावल को किस अनुपात में मिलाना चाहिए, एक की कीमत 20 रुपये/किलोग्राम और दूसरे की कीमत 10 रुपये/किलोग्राम है, ताकि उसे 14 रुपये/किलोग्राम की चावल की किस्म प्राप्त हो सके?
समाधान: यहां भी हम अलिगेशन का उपयोग कर सकते हैं:
- x = 14-10 = 4
- y = 20-14 = 6
प्रकार 1 और प्रकार 2 चावल के बीच का अनुपात 4:6 या 2:3 है।
इसे अलिगेशन का नियम भी कहा जाता है और इसे इस प्रकार व्यक्त किया जा सकता है:
अलिगेशन के अनुप्रयोग
समाधान: अलिगेशन के नियम द्वारा:
समाधान: कुल लाभ प्रतिशत = M%
अलिगेशन के नियम द्वारा:
समाधान: औसत गति = X
अलिगेशन के नियम द्वारा:
नोट: यात्रा के विभिन्न भागों पर गति का अलिगेशन का सिद्धांत लागू करने के बाद, हमें उन भागों को कवर करने में लगे समय का अनुपात मिलेगा।
समाधान: यात्रा की औसत गति = 360/6 = 60 किमी/घंटा
अलिगेशन के नियम द्वारा:
समाधान: 2 वर्षों के लिए उधार राशि पर प्रभावी ब्याज दर = 25% * 2 = 50%
(-30 – X): (X – 50) = 5000: 3000 = 5: 3
-90 – 3X = 5X – 250
8X = 160
X = 20
इसलिए, ब्याज राशि पर कुल लाभ = 20% का (5000 + 3000) = = ₹1600
समाधान: कक्षा की औसत आयु = A
समाधान: अलिगेशन के नियम द्वारा:
समाधान: अलिगेशन के नियम द्वारा:
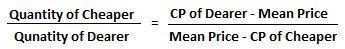
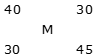
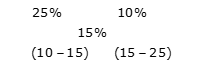
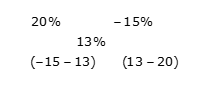

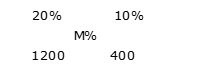
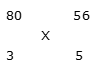
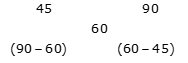
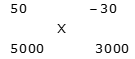
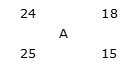
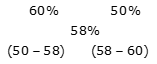
|
142 videos|172 docs|185 tests
|




















