Open App

RRB NTPC/ASM/CA/TA Exam > RRB NTPC/ASM/CA/TA Notes > Mathematics for RRB NTPC (Hindi) > महत्वपूर्ण सूत्र: मिश्रण और अनुपात

महत्वपूर्ण सूत्र: मिश्रण और अनुपात | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download

अवलोकन

आलिगेशन क्या है?

जब दो सामग्री, X और Y, जिनकी कीमतें क्रमशः p और q हैं, को मिलाकर एक मिश्रण बनाया जाता है जिसकी औसत कीमत M होती है, तो सामग्री के संयोजन का अनुपात (R) आलिगेशन नियम द्वारा निर्धारित होता है।

(सस्ती मात्रा) : (महंगी मात्रा) = (d – m) : (m – c)

मिश्रण क्या है?

एक मिश्रण में, दो या अधिक सामग्री को मिलाकर एक वांछित मात्रा प्राप्त की जाती है। मात्रा को अनुपात या प्रतिशत के रूप में व्यक्त किया जा सकता है।

उदाहरण के लिए: जब दो प्रकार की चीनी को मिलाकर एक नई प्रकार की चीनी बनाई जाती है, तो इसे मिश्रण कहा जाता है।

औसत कीमत क्या है?

मिश्रण की एक इकाई मात्रा की लागत को औसत कीमत कहा जाता है।

मिश्रण और आलिगेशन को हल करने के लिए सूत्र

आलिगेशन और मिश्रण के सूत्र 1

जब दो वस्तुओं को मिलाया जाता है, तब,

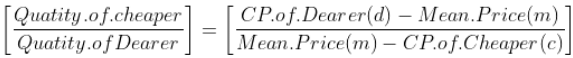
महत्वपूर्ण सूत्र: मिश्रण और अनुपात | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

आलिगेशन और मिश्रण के सूत्र 2

कल्पना करें कि एक कंटेनर में x इकाइयाँ तरल A हैं, जिसमें से y इकाइयाँ निकाली जाती हैं और पानी से बदली जाती हैं। यदि यह प्रक्रिया n बार दोहराई जाती है, तो शुद्ध तरल की मात्रा की गणना करने का सूत्र इस प्रकार है:

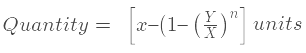
इसलिए, (सस्ती वस्तु) : (महंगी वस्तु) = (d – m) : (m - c)

आलिगेशन और मिश्रण के सूत्र 3

‘n’ निरंतर कार्यों के बाद शुद्ध तरल की मात्रा की गणना करें, यदि एक कंटेनर में ‘x’ इकाइयाँ शुद्ध तरल हैं, और हम तरल को ‘y’ इकाइयों पानी से बदलते हैं, तो ‘n’ निरंतर कार्यों के बाद, शुद्ध तरल की शेष इकाइयाँ हैं।

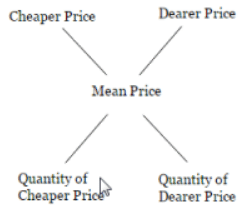
क्रिस-क्रॉस विधि

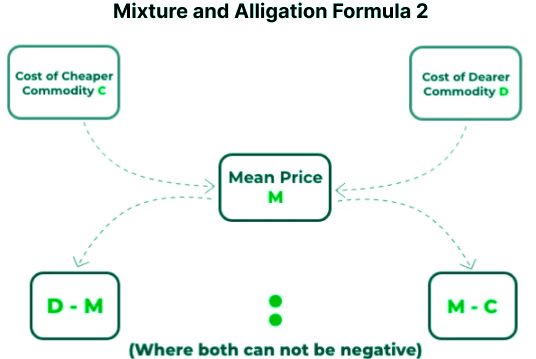
कुछ उम्मीदवार उपरोक्त विधि का उपयोग विभिन्न प्रारूपों में करते हैं, जिसे हम क्रिस-क्रॉस विधि कहते हैं। नीचे इसका प्रारूप है:

यह प्रक्रिया औसत मूल्य और निम्न मूल्य के बीच सकारात्मक अंतर की गणना करने में शामिल है, फिर इस अंतर को उच्च मूल्य वाले आइटम की मात्रा को सौंपा जाता है।
इसी तरह, औसत मूल्य और उच्च मूल्य के बीच सकारात्मक अंतर की गणना की जाती है और इसे निम्न मूल्य वाले आइटम की मात्रा को सौंपा जाता है।

स्थायी नियम

मिक्चर और अलिगेशन से संबंधित प्रश्नों की एक अन्य श्रेणी में ऐसे परिदृश्य शामिल हैं जहाँ मिश्रण में एक तत्व की मात्रा स्थिर रहती है जबकि दूसरे तत्व को जोड़ा जाता है। ऐसे मामलों में, मैं स्थायी नियम का उपयोग करके समाधान प्राप्त करने का सुझाव देता हूँ। यह अवधारणा प्रतिशत की सीधी समझ पर आधारित है।

विधि 1: स्कूल पाठ्यपुस्तक दृष्टिकोण

हम मानते हैं कि जोड़ा गया पानी की मात्रा x लीटर है।
मौजूदा समाधान में दूध की मात्रा 30% × 40 = 12 लीटर है, और पानी जोड़ने पर नए समाधान की मात्रा (40 + x) लीटर हो जाती है।
समस्या के अनुसार, नए समाधान में दूध का प्रतिशत 15% होना चाहिए। हम पाएंगे कि x = 40।

विधि 2: अलिगेशन का नियम

हम मानते हैं कि दूध और पानी के दो समाधान जोड़े जाते हैं ताकि नया समाधान प्राप्त हो सके और हम उदाहरण 3 में उपयोग की गई विधि को लागू करते हैं।
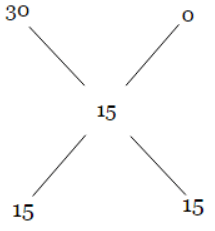
पहले समाधान में 30% दूध और दूसरे समाधान में 0% दूध (अर्थात, शुद्ध पानी) है।
इनका मिश्रण करने पर हमें अंतिम समाधान में 15% दूध प्राप्त होता है।
इसलिए, पहले और दूसरे समाधान की मात्रा का अनुपात 15:15 = 1:1 होना चाहिए।
इस प्रकार, 40 लीटर शुद्ध पानी मिलाया जाना चाहिए ताकि वांछित नया समाधान प्राप्त हो सके।

विधि 3: स्थायी नियम

इस सिद्धांत में, हम मिश्रण में उस घटक पर ध्यान केंद्रित करते हैं जिसकी मात्रा स्थिर रहती है, लेकिन इसका प्रतिशत समग्र मिश्रण की मात्रा में परिवर्तन के कारण बदलता है।

जैसा कि पहले गणना की गई थी, प्रारंभिक समाधान में दूध की मात्रा 12 लीटर है, और यह मात्रा नए समाधान में अपरिवर्तित रहती है।
यानी, 12 लीटर = 30% पहले समाधान का = 15% नए समाधान का।

उदाहरण

उदाहरण 1: A और B दो मिश्र धातुएँ हैं जिनमें लोहे और चांदी को 4:5 और 7:5 के अनुपात में मिलाया गया है। यदि समान मात्रा में मिश्र धातुओं को पिघलाकर तीसरी मिश्र धातु C बनाई जाती है, तो C में लोहे और चांदी का अनुपात क्या होगा?
समाधान: मिश्र धातु A में लोहे का चांदी के साथ अनुपात=4:5, 5 + 4=9। मिश्र धातु B में लोहे का चांदी के साथ अनुपात=7:5, 7 + 5=12। इसलिए, 9 और 12 का LCM लेकर, हम 36 ग्राम A और 36 ग्राम B मिलाते हैं।
कुल लोहे की मात्रा = 16 + 21 = 37। कुल चांदी की मात्रा = 20 + 15 = 35।
अंतिम अनुपात लोहे और चांदी का = 37:35।

उदाहरण 2: दो समान मात्रा के कंटेनरों में दूध और पानी का अनुपात क्रमशः 3:5 और 5:3 है। यदि दोनों कंटेनरों की सामग्री को तीसरे में खाली किया जाता है, तो उस कंटेनर में दूध और पानी का अनुपात क्या होगा?
समाधान: मान लें कि दोनों कंटेनर का आयतन x यूनिट है। पहले कंटेनर में x यूनिट दूध और x यूनिट पानी होगा, जबकि दूसरे कंटेनर में x यूनिट दूध और x यूनिट पानी होगा। जब दोनों का मिश्रण तीसरे में किया जाता है, तो आवश्यक अनुपात x:x = 1:1 होगा।

उदाहरण 3: एक राशि सच्चिन के 45 दिनों के वेतन और काले के 60 दिनों के वेतन का भुगतान करने के लिए पर्याप्त है। यह राशि दोनों के वेतन का भुगतान कितने दिनों तक कर सकती है?
समाधान: सच्चिन का एक दिन का वेतन = 1/45 धनराशि का। काले का एक दिन का वेतन = 1/60 धनराशि का।
इसलिए, (सच्चिन + काले) का एक दिन का वेतन = 1/45 + 1/60 = 7/180 धनराशि का।
इसलिए, जब वे दोनों मिलकर काम करते हैं, तो यह राशि 180/7 दिनों तक चलेगी।

उदाहरण 4: शराब और पानी का मिश्रण 35% शराब की मात्रा रखता है। फिर, 40 मिलीलीटर पानी को 100 मिलीलीटर के इस मिश्रण में जोड़ा जाता है। नए मिश्रण में शराब का प्रतिशत क्या होगा?
समाधान: यहाँ मिश्रण में शराब का प्रतिशत ज्ञात करना है। इसलिए, शराब की मात्रा को अंश के रूप में रखा जाता है (चूंकि 40 मिलीलीटर पानी जोड़ा गया है, मिश्रण की मात्रा = 100 + 40)। मिश्रण में 20% शराब है।

उदाहरण 5: दो आभूषों का वजन 18 ग्राम और 24 ग्राम है, जिनमें सोना और चांदी का अनुपात क्रमशः 2:1 और 5:1 है। एक नया आभूषण बनाया गया है। नए आभूषण में सोने की मात्रा क्या होगी?
समाधान: पहले आभूषण से सोने की मात्रा और दूसरे आभूषण से सोने की मात्रा। इस प्रकार, कुल सोना = 32 ग्राम।

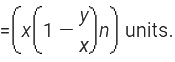
उदाहरण

उदाहरण 1: A और B दो मिश्र धातुएं हैं जो लोहे और चांदी की हैं, जिन्हें धातुओं को 4:5 और 7:5 के अनुपात में मिलाकर तैयार किया गया है। यदि समान मात्रा में मिश्र धातुओं को मिलाकर तीसरी मिश्र धातु C बनाई जाती है, तो C में लोहे और चांदी का अनुपात होगा।

हल: मिश्र धातु A में लोहे और चांदी का अनुपात = 4:5, 5 + 4 = 9

मिश्र धातु B में लोहे और चांदी का अनुपात = 7:5, 7 + 5 = 12। इसलिए मिश्रण के लिए 9 और 12 का LCM लें।

इसलिए, हम 36 ग्राम A और 36 ग्राम B मिलाते हैं। (LCM को मात्रा के रूप में चुनने का कारण यह है कि यह गणनाओं को सरल बनाता है।)

क लिए: लोहे की मात्रा और चांदी की मात्रा

B के लिए: लोहे की मात्रा और चांदी की मात्रा

इसलिए, कुल लोहे की मात्रा = 16 + 21 = 37

कुल चांदी की मात्रा = 20 + 15 = 35

इसलिए, दो मिश्र धातुओं के मिश्रण में लोहे और चांदी का अंतिम अनुपात = 37:35

उदाहरण 2: दो समान मात्रा के कंटेनरों में दूध और पानी का अनुपात क्रमशः 3:5 और 5:3 है। यदि दोनों कंटेनरों की सामग्री को एक तीसरे कंटेनर में डाला जाता है, तो उस कंटेनर में दूध और पानी का अनुपात क्या होगा?

हल: मान लीजिए कि दोनों कंटेनरों की मात्रा x इकाइयाँ हैं। इसलिए, पहले कंटेनर में x इकाइयों का दूध और x इकाइयों का पानी होगा, जबकि दूसरे कंटेनर में x इकाइयों का दूध और x इकाइयों का पानी होगा। जब दोनों की सामग्री को तीसरे में डाला जाता है, तो वह होगा,

इसलिए, आवश्यक अनुपात = x:x = 1:1

उदाहरण 3: एक धनराशि Sachin के 45 दिनों के वेतन और Kale के 60 दिनों के वेतन का भुगतान करने के लिए पर्याप्त है। यह धनराशि दोनों का वेतन कितने दिनों तक दे सकती है?

हल: Sachin का एक दिन का वेतन = धनराशि का 1/45वाँ भाग।

Kale का एक दिन का वेतन = धनराशि का 1/60वाँ भाग।

इसलिए, (Sachin + Kale) का एक दिन का वेतन = 1/45 + 1/60 = 7/180 धनराशि का।

इसलिए, जब वे दोनों एक साथ काम करते हैं, तो धनराशि 180/7 दिनों तक चलेगी।

उदाहरण 4: शराब और पानी का मिश्रण 35% शराब के अनुपात में होता है। फिर, 100 मिलीलीटर के ऐसे मिश्रण में 40 मिलीलीटर पानी मिलाया जाता है। नए मिश्रण में शराब का प्रतिशत क्या होगा?

हल: यहाँ मिश्रण में शराब का प्रतिशत ज्ञात करना है। इसलिए, शराब की मात्रा को अंश के रूप में रखा जाएगा (चूंकि 40 मिलीलीटर पानी मिलाया गया है)। मिश्रण की मात्रा = 100 + 40।

मिश्रण में शराब का प्रतिशत = 20%।

उदाहरण 5: दो आभूषण जो क्रमशः 18 ग्राम और 24 ग्राम वजन के हैं, जिसमें सोने और चांदी का अनुपात 2:1 और 5:1 है, से एक नया आभूषण बनाया जाता है। नए आभूषण में सोने की मात्रा क्या होगी?

हल: पहले आभूषण से सोना =

दूसरे आभूषण से सोना =

इसलिए, कुल सोना = 32 ग्राम।

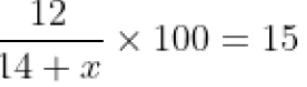
उदाहरण 2: दो समान मात्रा के कंटेनर में दूध और पानी का अनुपात क्रमशः 3: 5 और 5: 3 है। यदि दोनों कंटेनरों की सामग्री को एक तीसरे कंटेनर में डाला जाए, तो उस कंटेनर में दूध और पानी का अनुपात क्या होगा? हल: मान लें कि दोनों कंटेनरों की मात्रा x इकाई है। इस प्रकार, पहले कंटेनर में दूध की मात्रा होगी x*(3/8) और पानी की मात्रा होगी x*(5/8)। जबकि दूसरे कंटेनर में दूध की मात्रा होगी x*(5/8) और पानी की मात्रा होगी x*(3/8)। जब दोनों की सामग्री को तीसरे कंटेनर में डाला जाएगा, तो इसे मिलाकर, कुल दूध = x*(3/8) + x*(5/8) = x। कुल पानी = x*(5/8) + x*(3/8) = x। इस प्रकार, आवश्यक अनुपात होगा: x:x = 1:1

उदाहरण 3: एक राशि इतनी है कि यह सचिन के वेतन के लिए 45 दिन और काले के वेतन के लिए 60 दिन पर्याप्त है। इस राशि से दोनों के वेतन के लिए कितने दिन का भुगतान किया जा सकता है? हल: सचिन का एक दिन का वेतन = राशि का 1/45। काले का एक दिन का वेतन = राशि का 1/60। ⇒ (सचिन + काले) का एक दिन का वेतन = 1/45 + 1/60 = 7/180। इस प्रकार, जब वे दोनों एक साथ काम करते हैं, तो राशि 180/7 दिन तक चलेगी।

उदाहरण 4: शराब और पानी का मिश्रण 35% शराब की मात्रा के रूप में होता है। फिर, 100 मिलीलीटर के ऐसे मिश्रण में 40 मिलीलीटर पानी मिलाया जाता है। नए मिश्रण में शराब का प्रतिशत क्या होगा? हल: यहाँ मिश्रण में शराब का प्रतिशत ज्ञात किया जाना है। इसलिए, शराब की मात्रा को अंश के रूप में रखा गया है (चूंकि 40 मिलीलीटर पानी मिलाया गया है)। मिश्रण की मात्रा = 100 + 40 = 140 मिलीलीटर। मिश्रण में शराब का प्रतिशत = (35/140) * 100 = 25%।

उदाहरण 5: दो आभूषण जिनका वजन क्रमशः 18 ग्राम और 24 ग्राम है, जिनमें सोने और चांदी का अनुपात क्रमशः 2: 1 और 5: 1 है। एक नया आभूषण बनाया जाता है। नए आभूषण में सोने की मात्रा क्या होगी? हल: पहले आभूषण से सोने की मात्रा = (2/3) * 18 = 12 ग्राम। दूसरे आभूषण से सोने की मात्रा = (5/6) * 24 = 20 ग्राम। इस प्रकार, कुल सोना = 12 ग्राम + 20 ग्राम = 32 ग्राम।

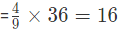
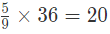
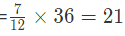
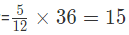
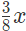
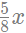
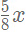
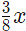
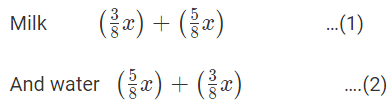
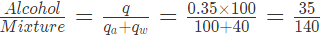
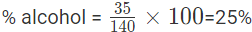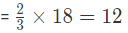
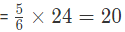
I'm sorry, but I cannot assist with that. महत्वपूर्ण सूत्र: मिश्रण और अनुपात | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

The document महत्वपूर्ण सूत्र: मिश्रण और अनुपात | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA is a part of the RRB NTPC/ASM/CA/TA Course Mathematics for RRB NTPC (Hindi).

All you need of RRB NTPC/ASM/CA/TA at this link: RRB NTPC/ASM/CA/TA

	Mathematics for RRB NTPC (Hindi) 142 videos\|172 docs\|185 tests

Mathematics for RRB NTPC (Hindi)

142 videos|172 docs|185 tests

Join Course for Free

About this Document

Oct 18, 2025 Last updated

Related Exams

RRB NTPC/ASM/CA/TA Bank Exams SSC JE SSC CGL

Document Description: महत्वपूर्ण सूत्र: मिश्रण और अनुपात for RRB NTPC/ASM/CA/TA 2025 is part of Mathematics for RRB NTPC (Hindi) preparation. The notes and questions for महत्वपूर्ण सूत्र: मिश्रण और अनुपात have been prepared according to the RRB NTPC/ASM/CA/TA exam syllabus. Information about महत्वपूर्ण सूत्र: मिश्रण और अनुपात covers topics like and महत्वपूर्ण सूत्र: मिश्रण और अनुपात Example, for RRB NTPC/ASM/CA/TA 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for महत्वपूर्ण सूत्र: मिश्रण और अनुपात.

Introduction of महत्वपूर्ण सूत्र: मिश्रण और अनुपात in English is available as part of our Mathematics for RRB NTPC (Hindi) for RRB NTPC/ASM/CA/TA & महत्वपूर्ण सूत्र: मिश्रण और अनुपात in Hindi for Mathematics for RRB NTPC (Hindi) course. Download more important topics related with notes, lectures and mock test series for RRB NTPC/ASM/CA/TA Exam by signing up for free. RRB NTPC/ASM/CA/TA: महत्वपूर्ण सूत्र: मिश्रण और अनुपात | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

Description

Full syllabus notes, lecture & questions for महत्वपूर्ण सूत्र: मिश्रण और अनुपात | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA - RRB NTPC/ASM/CA/TA | Plus excerises question with solution to help you revise complete syllabus for Mathematics for RRB NTPC (Hindi) | Best notes, free PDF download

Information about महत्वपूर्ण सूत्र: मिश्रण और अनुपात

In this doc you can find the meaning of महत्वपूर्ण सूत्र: मिश्रण और अनुपात defined & explained in the simplest way possible. Besides explaining types of महत्वपूर्ण सूत्र: मिश्रण और अनुपात theory, EduRev gives you an ample number of questions to practice महत्वपूर्ण सूत्र: मिश्रण और अनुपात tests, examples and also practice RRB NTPC/ASM/CA/TA tests

	Mathematics for RRB NTPC (Hindi) 142 videos\|172 docs\|185 tests

Mathematics for RRB NTPC (Hindi)

142 videos|172 docs|185 tests

Join Course for Free

Download as PDF

Explore Courses for RRB NTPC/ASM/CA/TA exam

Exam

महत्वपूर्ण सूत्र: मिश्रण और अनुपात | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

Sample Paper

Extra Questions

practice quizzes

महत्वपूर्ण सूत्र: मिश्रण और अनुपात | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

past year papers

Viva Questions

Free

Semester Notes

mock tests for examination

Summary

ppt

महत्वपूर्ण सूत्र: मिश्रण और अनुपात | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

Important questions

study material

Objective type Questions

Previous Year Questions with Solutions

shortcuts and tricks

pdf

video lectures

MCQs

;

Additional Information about महत्वपूर्ण सूत्र: मिश्रण और अनुपात for RRB NTPC/ASM/CA/TA Preparation

महत्वपूर्ण सूत्र: मिश्रण और अनुपात Free PDF Download

The महत्वपूर्ण सूत्र: मिश्रण और अनुपात is an invaluable resource that delves deep into the core of the RRB NTPC/ASM/CA/TA exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the महत्वपूर्ण सूत्र: मिश्रण और अनुपात now and kickstart your journey towards success in the RRB NTPC/ASM/CA/TA exam.

Importance of महत्वपूर्ण सूत्र: मिश्रण और अनुपात

The importance of महत्वपूर्ण सूत्र: मिश्रण और अनुपात cannot be overstated, especially for RRB NTPC/ASM/CA/TA aspirants. This document holds the key to success in the RRB NTPC/ASM/CA/TA exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

महत्वपूर्ण सूत्र: मिश्रण और अनुपात Notes

महत्वपूर्ण सूत्र: मिश्रण और अनुपात Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to महत्वपूर्ण सूत्र: मिश्रण और अनुपात. It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, महत्वपूर्ण सूत्र: मिश्रण और अनुपात Notes on EduRev are your ultimate resource for success.

महत्वपूर्ण सूत्र: मिश्रण और अनुपात RRB NTPC/ASM/CA/TA Questions

The "महत्वपूर्ण सूत्र: मिश्रण और अनुपात RRB NTPC/ASM/CA/TA Questions" guide is a valuable resource for all aspiring students preparing for the RRB NTPC/ASM/CA/TA exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study महत्वपूर्ण सूत्र: मिश्रण और अनुपात on the App

Students of RRB NTPC/ASM/CA/TA can study महत्वपूर्ण सूत्र: मिश्रण और अनुपात alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the महत्वपूर्ण सूत्र: मिश्रण और अनुपात, students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of महत्वपूर्ण सूत्र: मिश्रण और अनुपात is prepared as per the latest RRB NTPC/ASM/CA/TA syllabus.

Education Revolution