महत्वपूर्ण समीकरण: रैखिक समीकरण | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download

रैखिक समीकरणों के सूत्रों का परिचय

एक रैखिक समीकरण, जो एक बीजगणितीय समीकरण के समान है जहाँ प्रत्येक पद का घातांक एक होता है, को ग्राफ़ के द्वारा एक सीधी रेखा के रूप में दर्शाया जाता है। रैखिक समीकरण का मानक रूप है: y = mx + b, जहाँ x एक चर है, और y, m, और b स्थिरांक हैं।

रैखिक समीकरणों के लिए सूत्र और परिभाषाएँ

• एक रैखिक समीकरण एक बीजगणितीय अभिव्यक्ति है जहाँ प्रत्येक पद का घातांक एक होता है, और इसका ग्राफ एक सीधी रेखा बनाता है।
• रैखिक समीकरण का मानक रूप है: y = mx + b, जहाँ x एक चर है, और y, m, और b स्थिरांक हैं।

रैखिक समीकरणों के रूप

रैखिक समीकरण के मुख्यतः 3 रूप होते हैं:

• मानक रूप
• ढलान-इंटरसेप्ट रूप
• पॉइंट-ढलान रूप

1. मानक रूप
रैखिक समीकरण का मानक रूप आमतौर पर इस प्रकार लिखा जाता है: Ax + By = C। जहाँ:

• A और B गुणांक (स्थिरांक) हैं जो क्रमशः x और y पदों के गुणांक का प्रतिनिधित्व करते हैं।
• C एक स्थिरांक है।

मानक रूप के लिए आवश्यक है कि A और B दोनों पूर्णांक हों और A नकारात्मक न हो। साथ ही, A और B के पास 1 के अलावा कोई सामान्य गुणक नहीं होना चाहिए। यह रूप बीजगणितीय हेरफेर और रैखिक समीकरणों के प्रणालियों को हल करने में सामान्यतः उपयोग किया जाता है।

2. ढलान-इंटरसेप्ट रूप
रैखिक समीकरण का ढलान-इंटरसेप्ट रूप इस प्रकार लिखा जाता है: y = mx + b। जहाँ:

• m रेखा की ढलान है, जो y और x के बीच परिवर्तन की दर को दर्शाता है।
• b y-इंटरसेप्ट है, जो y का मान है जब x 0 के बराबर होता है। यह वह बिंदु है जहाँ रेखा y-अक्ष को काटती है।

यह रूप रैखिक समीकरणों को ग्राफ़ करने और रेखा की ढलान और y-इंटरसेप्ट को जल्दी पहचानने के लिए विशेष रूप से उपयोगी है।

3. पॉइंट-स्लोप फॉर्म एक रैखिक समीकरण का पॉइंट-स्लोप फॉर्म इस प्रकार दिया गया है:

y − y1 = m(x − x1)

• m रेखा का ढलान है, जैसा कि ढलान-इंटरसेप्ट फॉर्म में समझाया गया है।
• (x1, y1) रेखा पर एक बिंदु के निर्देशांक को दर्शाता है।

यह फॉर्म तब उपयोगी है जब आपको रेखा पर एक विशेष बिंदु और उसका ढलान ज्ञात हो, जिससे आप सीधे समीकरण लिख सकते हैं बिना y-इंटरसेप्ट की गणना किए।

एक चर में रैखिक समीकरण

• एक चर में रैखिक समीकरण को इस प्रकार परिभाषित किया गया है: ax + b = 0
• जहाँ, a और b स्थिरांक हैं, a ≠ 0, और x एक अज्ञात चर है।
• समीकरण ax + b = 0 का समाधान x है। हम यह भी कह सकते हैं कि यह रैखिक समीकरण ax + b = 0 का मूल है।

दो चर में रैखिक समीकरण

• दो चर में रैखिक समीकरण को इस प्रकार परिभाषित किया गया है: ax + by + c = 0
• जहाँ a, b, और c स्थिरांक हैं और a और b दोनों ≠ 0 हैं।

तीन चर में रैखिक समीकरण

• तीन चर में रैखिक समीकरण को इस प्रकार परिभाषित किया गया है: ax + by + cz = d
• जहाँ a, b, c, और d स्थिरांक हैं और a, b और c सभी ≠ 0 हैं।

रैखिक समीकरणों को हल करने के लिए सूत्र और विधियाँ

उपस्थापन विधि

• चरण 1: किसी एक समीकरण को x या y के लिए हल करें।
• चरण 2: चरण 1 से प्राप्त समाधान को दूसरे समीकरण में प्रतिस्थापित करें।
• चरण 3: अब इस समीकरण को दूसरे चर के लिए हल करें।

उन्मूलन विधि

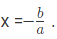
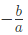
चरण 1: दोनों समीकरणों को ऐसे संख्याओं से गुणा करें कि दो अज्ञातों में से एक का गुणांक एक समान हो जाए।

चरण 2: पहले समीकरण से दूसरे समीकरण को घटाएं।

चरण 3: किसी भी एक समीकरण में अज्ञात चर का मान रखकर, दूसरे अज्ञात चर का मान ज्ञात करें।

क्रॉस-मल्टीप्लिकेशन विधि

मान लीजिए, दो समीकरण हैं,

• समीकरण (1) को p₂ से गुणा करें।
• समीकरण (2) को p₁ से गुणा करें।
• घटाने पर, जहाँ (p₁q₂ – p₂q₁) ≠ 0।
• समीकरण (1) को q₂ से गुणा करें।
• समीकरण (2) को q₁ से गुणा करें।
• घटाने पर, जहाँ (p₁q₂ – p₂q₁) ≠ 0।

समीकरण (3) और (4) से, हमें मिलता है, जहाँ (p₁q₂ – p₂q₁) ≠ 0।

नोट: इस समीकरण को हल करने का शॉर्टकट इस प्रकार लिखा जाएगा, जिसका अर्थ है,

रेखीय समीकरणों के महत्वपूर्ण सूत्र और याद रखने योग्य मुख्य बिंदु

मान लीजिए, दो रेखीय समीकरण हैं: a₁x + b₁y = c₁ और a₂x + b₂y = c₂

• (a) यदि a₁/a₂ ≠ b₁/b₂, तो एक समाधान होगा, और ग्राफ़ में रेखाएँ परस्पर मिलेंगी।
• (b) यदि a₁/a₂ = b₁/b₂, तो अनेक समाधान होंगे, और ग्राफ़ में रेखाएँ समन्वित होंगी।
• (c) यदि a₁/a₂ = b₁/b₂ ≠ c₁/c₂, तो कोई समाधान नहीं होगा, और ग्राफ़ में रेखाएँ समानांतर होंगी।

रेखीय समीकरणों के सूत्रों पर प्रश्न

प्रश्न 1: रेखा के समीकरण का ढलान-इंटरसेप्ट रूप क्या है?

• (a) y = mx + b
• (b) y = mx – b
• (c) y = bx + m
• (d) y = bx – m

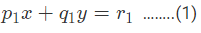
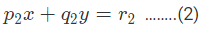
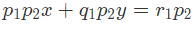
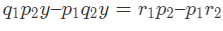
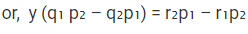
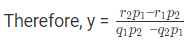
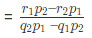
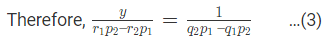
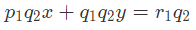
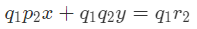
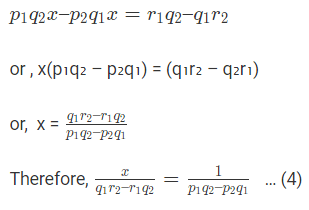
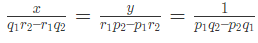
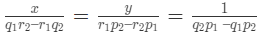
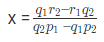
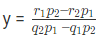
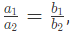
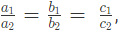
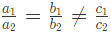
प्रश्न 2: एक रेखीय समीकरण का मानक रूप कैसा दिखता है? (a) y = mx b (b) y = bx m (c) Ax By = C (d) Ax By = D उत्तर: (c) एक रेखीय समीकरण का मानक रूप Ax By = C है, जहाँ A और B क्रमशः x और y के गुणांक हैं, और C एक स्थिरांक है।

प्रश्न 3: आप एक रेखीय समीकरण से भिन्नों को कैसे समाप्त कर सकते हैं? (a) समीकरण के दोनों पक्षों को एक सामान्य हर के द्वारा गुणा करें (b) समीकरण के दोनों पक्षों को एक सामान्य हर से भाग दें (c) समीकरण के दोनों पक्षों में एक सामान्य हर जोड़ें (d) समीकरण के दोनों पक्षों से एक सामान्य हर घटाएं उत्तर: (a) एक रेखीय समीकरण से भिन्नों को समाप्त करने के लिए, समीकरण के दोनों पक्षों को एक सामान्य हर के द्वारा गुणा करें। यह प्रक्रिया भिन्नों को समाप्त कर देगी और समीकरण को हल करना आसान बना देगी।

प्रश्न 4: किस प्रकार का रेखीय समीकरण तब उपयोगी होता है जब आप रेखा पर एक विशिष्ट बिंदु और उसकी ढलान जानते हैं? (a) बिंदु-ढलान रूप (b) ढलान-प्रतिच्छेदन रूप (c) मानक रूप (d) उपरोक्त में से कोई नहीं उत्तर: (a) रेखीय समीकरण का बिंदु-ढलान रूप y − y1 = m(x − x1) के रूप में लिखा जाता है, जहाँ (x1, y1) रेखा पर एक बिंदु के निर्देशांक हैं, और m ढलान है।

प्रश्न 5: निम्नलिखित में से रेखीय समीकरण के बिंदु-ढलान रूप का सही प्रतिनिधित्व कौन सा है? (a) y = mx b (b) y − y1 = m(x − x1) (c) y = Ax By (d) y = m1x b उत्तर: (b) रेखीय समीकरण का बिंदु-ढलान रूप y − y1 = m(x − x1) के रूप में दर्शित किया जाता है, जहाँ (x1, y1) रेखा पर एक बिंदु के निर्देशांक हैं, और m रेखा की ढलान है। यह रूप तब उपयोगी होता है जब आप रेखा पर एक विशिष्ट बिंदु और उसकी ढलान जानते हैं।