रेखीय समीकरण: महत्वपूर्ण सिद्धांत | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download

रेखीय समीकरण क्या है?

रेखीय समीकरण वह समीकरण है जो ग्राफ पर चित्रित करने पर सीधी रेखा देता है।

• रेखीय समीकरण एक चर, दो चर या तीन चर के हो सकते हैं।
• माना कि a, b, c और d स्थिरांक हैं और x, y और z चर हैं। एकल चर रेखीय समीकरण का सामान्य रूप ax + b = 0 है।
• दो चर रेखीय समीकरण का सामान्य रूप ax + by = c है।
• तीन चर रेखीय समीकरण का सामान्य रूप ax + by + cz = d है।

दो चर में रेखीय समीकरण

• दो चर में रेखीय समीकरण उस रूप का समीकरण है ax + by + c = 0, जहाँ x और y दो चर हैं और a, b, और c वास्तविक संख्याएँ हैं और a और b शून्य नहीं हैं।
• इसे लोकप्रिय रूप से समानांतर रेखीय समीकरण के रूप में जाना जाता है।
• दो चर में रेखीय समीकरणों का उपयोग ज्यामिति में सीधी रेखा के निर्देशांक खोजने के लिए किया जाता है।

दो चर में रेखीय समीकरणों के रूप

दो चर में रेखीय समीकरण ऐसे समीकरण हैं जिनके अद्वितीय समाधान, कोई समाधान नहीं, या अनंत समाधान हो सकते हैं। ये विभिन्न रूपों में उपस्थित हो सकते हैं:

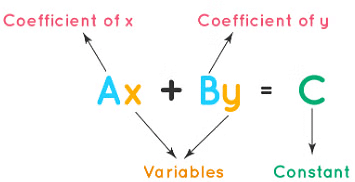
• मानक रूप (Standard Form)
• इंटरसेप्ट रूप (Intercept Form)
• पॉइंट-स्लोप रूप (Point-Slope Form)

1. दो चर में रैखिक समीकरणों का मानक रूप

• मानक रूप में समीकरण का प्रारूप है: ax + by + c = 0। यहाँ a, b और c गुणांक स्थिरांक हैं।
• एक समीकरण के रूप में मान लें: 3x + 4y = 11। मानक रूप में समीकरण को इस प्रकार प्रस्तुत किया जाता है: 3x + 4y - 11 = 0।

2. दो चर में रैखिक समीकरणों का इंटरसेप्ट रूप

• इंटरसेप्ट रूप में समीकरण का प्रारूप है: y = mx + b।
• उसी समीकरण के लिए, 3x + 4y = 11। इंटरसेप्ट या स्लोप-इंटरसेप्ट रूप में समीकरण को इस प्रकार प्रस्तुत किया जाता है: y = (-3/4)x + 11/4।

3. दो चर में रैखिक समीकरणों का पॉइंट-स्लोप रूप

• पॉइंट-स्लोप रूप में समीकरण का प्रारूप है: y − y1 = m(x − x1)।
• यहाँ m = ढलान (slope) है और (x1, y1) उन बिंदुओं का प्रतिनिधित्व करता है जो दी गई रेखा पर हैं।
• पॉइंट-स्लोप रूप का एक उदाहरण: y - 4 = 5(x - 3)। यहाँ 5 ढलान है और (3, 4) दी गई रेखा पर एक बिंदु है।

दो चर में समवर्ती रैखिक समीकरणों की प्रणाली

हम दो चर वाले दो रेखीय समीकरणों पर विचार करें, a1x + b1y + c1 = 0 और a2x + b2y + c2 = 0। इन दो समीकरणों को समकालिक रेखीय समीकरणों के एक समूह या सरलता से रेखीय समीकरणों के एक जोड़े के रूप में जाना जाता है।

उदाहरण: x + y - 3 = 0 और 2x - 5y + 1 = 0 दो चर x और y में दो समकालिक रेखीय समीकरणों का एक जोड़ा है। समाधान: दो चर वाले रेखीय समीकरणों के एक जोड़े का समाधान उन संख्याओं के क्रमबद्ध युग्म (ordered pair) के रूप में होता है जो दोनों समीकरणों को संतोष प्रदान करता है। उपरोक्त उदाहरण के लिए, x = 2 और y = 1 इस रेखीय समीकरणों के जोड़े का समाधान है। हम इसे प्रत्येक समीकरण में x = 2 और y = 1 को प्रतिस्थापित करके सत्यापित कर सकते हैं। दो चर वाले रेखीय समीकरणों का ग्राफिकल प्रतिनिधित्व हमेशा दो सीधी रेखाओं द्वारा दिया जाता है, जो या तो काटने वाली रेखाएँ, समानांतर रेखाएँ या सहसामान्य रेखाएँ होती हैं।

दो चर वाले रेखीय समीकरणों के समाधान की प्रकृति

• दो चर वाले रेखीय समीकरणों के एक समूह में एक समाधान हो सकता है या कोई समाधान नहीं हो सकता है या अनंत समाधान हो सकते हैं।
• यदि रेखीय समीकरणों का समूह एक समाधान रखता है, तो इसे संगत (consistent) कहा जाता है, जिसका अर्थ है कि कम से कम एक मान सेट सभी समीकरणों को संतोष प्रदान करता है। दूसरी ओर, एक असंगत (inconsistent) समूह में कोई समाधान नहीं होता, यह दर्शाता है कि कोई मान सेट सभी समीकरणों को एक साथ संतोष प्रदान नहीं कर सकता।
• इसी प्रकार, एक रेखीय समीकरणों का समूह स्वतंत्र (independent) माना जाता है यदि इसमें एक अद्वितीय समाधान होता है, जिसका अर्थ है कि चर के मान को अद्वितीय रूप से निर्धारित किया जा सकता है। इसके विपरीत, एक निर्भर (dependent) समूह में अनंत संख्या में समाधान होते हैं।

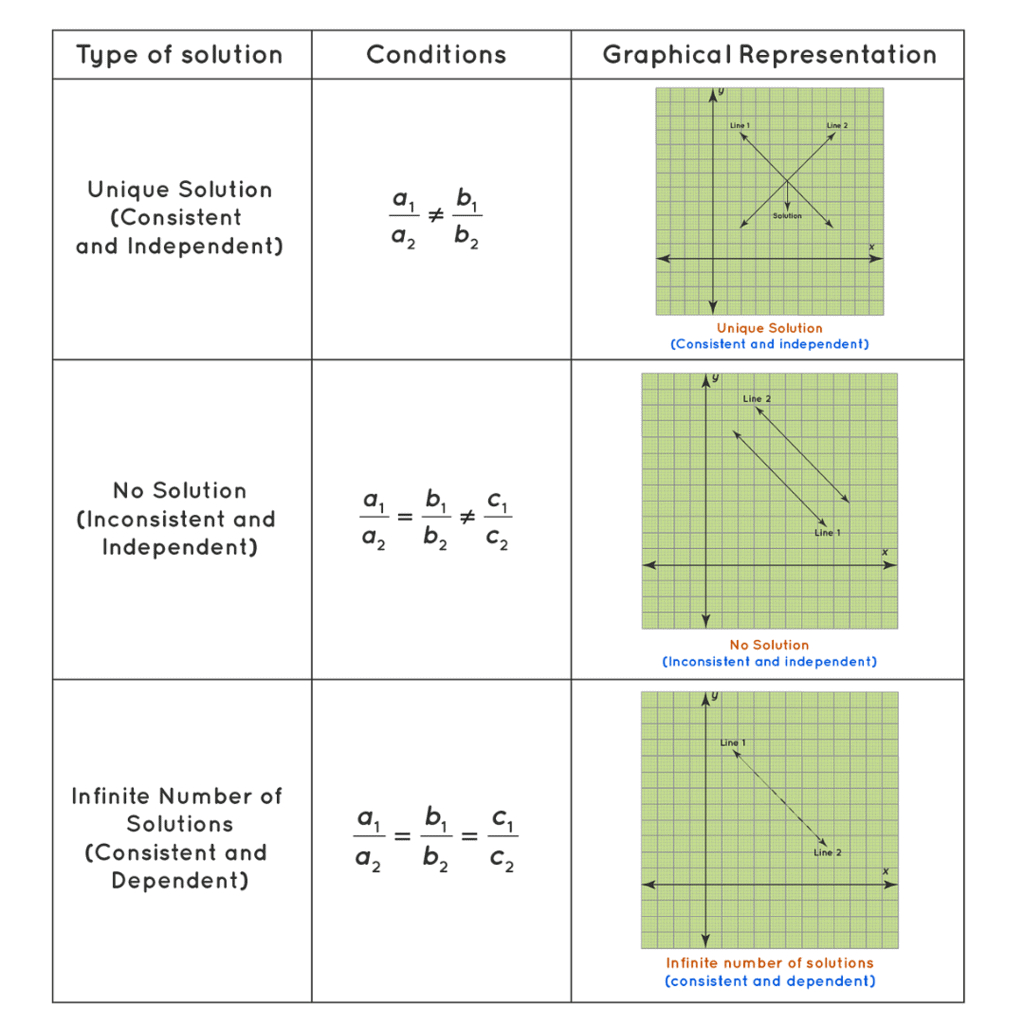
1. दो चर वाले रेखीय समीकरणों का अद्वितीय समाधान

दो चर में रैखिक समीकरणों का एक प्रणाली तब एक अद्वितीय समाधान रखती है जब और केवल जब समीकरण दो गैर-समांतर रेखाओं का प्रतिनिधित्व करते हैं जो केवल एक बिंदु पर मिलती हैं। दूसरे शब्दों में, रेखाओं की ढलान अलग होनी चाहिए, जो यह इंगित करती है कि वे समांतर नहीं हैं, और उन्हें केवल एक बिंदु पर ही मिलना चाहिए। इसलिए, यदि m1 और m2 दो रेखाओं के समीकरणों की ढलान हैं, तो समीकरणों के अद्वितीय समाधान के लिए m1 को m2 के बराबर नहीं होना चाहिए, अर्थात् m1 ≠ m2। अद्वितीय समाधान को विभिन्न तरीकों का उपयोग करके समीकरणों को एक साथ हल करके पाया जा सकता है, जिसमें प्रतिस्थापन, उन्मूलन, या मैट्रिसेस शामिल हैं। यह ध्यान रखना महत्वपूर्ण है कि रैखिक समीकरणों की एक प्रणाली में शून्य समाधान या अनंत समाधान हो सकते हैं यदि रेखाएँ समांतर या एक-दूसरे के साथ मेल खाती हैं।

• दो चर में रैखिक समीकरणों का एक प्रणाली तब एक अद्वितीय समाधान रखती है जब और केवल जब समीकरण दो गैर-समांतर रेखाओं का प्रतिनिधित्व करते हैं जो केवल एक बिंदु पर मिलती हैं।
• इसलिए, यदि m1 और m2 दो रेखाओं के समीकरणों की ढलान हैं, तो m1 को m2 के बराबर नहीं होना चाहिए, अर्थात् m1 ≠ m2।

2. दो चर में रैखिक समीकरणों का कोई समाधान नहीं

दो चर में रैखिक समीकरणों का एक प्रणाली तब कोई समाधान नहीं रखती है जब और केवल जब समीकरण दो समांतर रेखाओं का प्रतिनिधित्व करते हैं जो मिलती नहीं हैं। दूसरे शब्दों में, रेखाओं की ढलान समान होनी चाहिए, जो यह दर्शाती है कि वे समांतर हैं, और वे मिलती नहीं हैं। इसे गणितीय रूप से m1 = m2 के रूप में दर्शाया जा सकता है, जहाँ m1 और m2 रेखाओं की ढलान हैं। जब रैखिक समीकरणों की एक प्रणाली में कोई समाधान नहीं होता है, तो इसका मतलब है कि कोई भी मान नहीं है जो प्रत्येक चर के लिए दोनों समीकरणों को एक साथ संतुष्ट करता है। इस स्थिति को अक्सर असंगत प्रणाली कहा जाता है, और यह तब उत्पन्न होती है जब समीकरणों द्वारा प्रदर्शित रेखाएँ एक-दूसरे को पार नहीं करती हैं।

• इसे गणितीय रूप से m1 = m2 के रूप में दर्शाया जा सकता है, जहाँ m1 और m2 रेखाओं की ढलान हैं।

3. दो चर में रैखिक समीकरणों के अनंत समाधान

• यह ध्यान रखना महत्वपूर्ण है कि एक रैखिक समीकरणों का प्रणाली अनंत संख्या में समाधान हो सकता है यदि समीकरण एक ही रेखा का प्रतिनिधित्व करते हैं या सह-coincident रेखाएं हैं।
• ऐसे मामलों में, एक रैखिक समीकरण दूसरे समीकरण का scalar गुणांक होता है, जैसे कि x y = 2 और 2x + 2y = 4 के मामले में।

दो चर में रैखिक समीकरणों को हल करने की प्रक्रिया

दो चर में रैखिक समीकरणों को हल करने के विभिन्न तरीके नीचे दिए गए हैं:

• स्थानांतरण विधि
• उन्मूलन विधि
• क्रॉस-मल्टीप्लिकेशन विधि
• ग्राफिकल विधि
• डिटरमिनेंट विधि

1. दो चर में रैखिक समीकरणों को हल करने के लिए स्थानांतरण विधि

स्थानांतरण विधि के माध्यम से दो चर में रैखिक समीकरणों को हल करने की प्रक्रिया इस प्रकार है:

• चरण 1. दिए गए समीकरणों में से एक को हल करें ताकि किसी एक चर का मान दूसरे के संदर्भ में प्राप्त किया जा सके, जो भी सुविधाजनक हो।
• चरण 2. प्राप्त चर के मान को दूसरे समीकरण में स्थानांतरित करें।
• चरण 3. प्राप्त एकल चर समीकरण को हल करें। अब इस मान को दो मूल समीकरणों में से किसी एक में स्थानांतरित करें और दूसरे चर के मान को प्राप्त करने के लिए हल करें।

उदाहरण 1. निम्नलिखित रैखिक समीकरणों के प्रणाली को हल करें: 4x - 3y = 8, x - 2y = -3

हल: दिए गए समीकरण हैं 4x - 3y = 8 ……….(i) और x - 2y = -3 ……….(ii) हम किसी भी समीकरण को किसी भी चर के लिए हल कर सकते हैं। लेकिन भिन्नों से बचने के लिए, हम दूसरे समीकरण को x के लिए हल करते हैं, x = 2y - 3 ……….(iii) समीकरण (i) में x का यह मान स्थानांतरित करते हैं, हमें मिलता है: 4(2y - 3) - 3y = 8, 8y - 12 - 3y = 8, 5y = 20, y = 4। इस y के मान को (ii) में स्थानांतरित करते हैं, हमें मिलता है: x - 24 = -3, x - 8 = -3, x = 5। अतः, समाधान है x = 5, y = 4।

उदाहरण 2. निम्नलिखित रैखिक समीकरणों को हल करें: 8x + 5y = 9, 3x + 2y = 4।
हल: दिए गए समीकरण हैं 8x + 5y = 9 ……….(i) 3x + 2y = 4 ……….(ii) समीकरण (ii) से, हमें मिलता है 2y = 4 - 3x। इस y के मान को (i) में प्रतिस्थापित करने पर हमें मिलता है। इस x के मान को समीकरण (ii) में प्रतिस्थापित करने पर हमें मिलता है 3(-2) + 2y = 4।
2y = 10 y = 5। इसलिए, समाधान है x = -2, y = 5।

2. दो चर में रैखिक समीकरणों को हल करने के लिए उन्मूलन विधि

यह विधि किसी एक चर को उन्मूलित करने का उपयोग करती है। यह विधि आमतौर पर प्रतिस्थापन विधि की तुलना में अधिक सुविधाजनक होती है। उन्मूलन विधि का उपयोग करके समीकरणों को हल करने का एक सरल तरीका यह है कि यदि x या y में से किसी एक का गुणांक किसी एक समीकरण में 1 है, तो उस समीकरण के दोनों पक्षों को दूसरे समीकरण में उसी चर के गुणांक से गुणा करें। आगे, उस चर को उन्मूलित करने के लिए जोड़ना या घटाना (संकेत के अनुसार) करें।

दो चर में रैखिक समीकरणों को हल करने के लिए उन्मूलन विधि की प्रक्रिया:

• चरण 1. एक या दोनों समीकरणों को (यदि आवश्यक हो) इस तरह से एक उपयुक्त संख्या से गुणा करें कि जोड़ने या घटाने पर एक चर उन्मूलित हो जाए।
• चरण 2. परिणामी एकल चर समीकरण को हल करें ताकि इस चर का मान ज्ञात हो। अब इस मान को दो मूल समीकरणों में से किसी एक में प्रतिस्थापित करें और उस चर का मान ज्ञात करने के लिए इसे हल करें जो पहले उन्मूलित हुआ था।

3. दो चर में रैखिक समीकरणों को हल करने के लिए क्रॉस-मल्टिप्लिकेशन विधि

दो चर में रैखिक समीकरणों को हल करने के लिए क्रॉस-मल्टिप्लिकेशन विधि की प्रक्रिया:

मान लें कि समानांतर रैखिक समीकरणों का समूह है a1x + b1y + c1 = 0, a2x + b2y + c2 = 0। इस रैखिक समीकरणों के समूह को क्रॉस-मल्टिप्लिकेशन विधि से हल करने के लिए, समाधान दिया गया है:

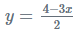
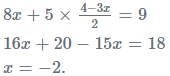
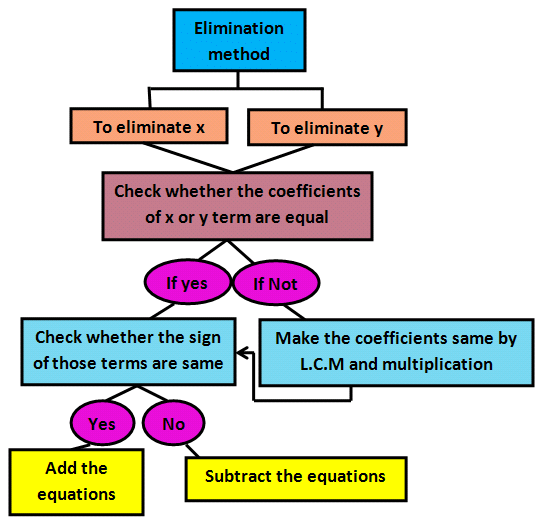
4. दो चर में रेखीय समीकरणों को हल करने की ग्राफिकल विधि

दो चर में रेखीय समीकरणों को हल करने की अगली विधि ग्राफिकल दृष्टिकोण है। दो रेखीय समीकरणों को ग्राफ के माध्यम से हल करने के लिए, हम निम्नलिखित चरणों का पालन करेंगे:

• चरण 1: हम ग्राफ पर दो समीकरणों का ग्राफ बनाने से शुरू करेंगे।
• चरण 2: ग्राफ को मैन्युअल रूप से प्लॉट करने के लिए समीकरणों को y = mx + b या x = my + b के रूप में परिवर्तित करें।
• चरण 3: x के विभिन्न मान जैसे 0, 1, 2,… को प्रतिस्थापित करें और संबंधित y के मान प्राप्त करें, या इसके विपरीत x के विभिन्न मान प्राप्त करने के लिए।
• चरण 4: समीकरण के विभिन्न बिंदुओं को ग्राफ पर प्लॉट करें और उस बिंदु का पता लगाने का प्रयास करें जहाँ दोनों रेखाएँ एक-दूसरे को काटती हैं।
• चरण 5: मिलन बिंदु दिए गए समीकरणों के समूह का उत्तर है।

यह हमेशा संभव नहीं है कि दोनों रेखाएँ एक-दूसरे को काटें, वे समानांतर भी हो सकती हैं या एक-दूसरे के साथ मेल खा सकती हैं। ऐसी स्थिति में, हम निम्नलिखित निष्कर्षों का पालन कर सकते हैं:

• यदि हमें दो रेखीय समीकरणों का एक सेट दिया गया है: a1x + b1y + c1 = 0 और a2x + b2y + c2 = 0
• यदि a1/a2 ≠ b1/b2: ऐसी स्थिति में एक अद्वितीय समाधान प्राप्त होता है और दिए गए रेखाओं का सेट एक बिंदु पर काटता है।
• यदि a1/a2 = b1/b2 ≠ c1/c2: ऐसी स्थिति में समीकरणों का समूह कोई समाधान नहीं है और रेखाएँ एक-दूसरे के समानांतर हैं।
• यदि a1/a2 = b1/b2 = c1/c2: उपरोक्त स्थिति के लिए, समीकरणों का समूह अनंत संख्या में समाधानों का होता है और दिए गए दो रेखाएँ एक-दूसरे के साथ मेल खाती हैं। यदि समूह में एक समाधान है, तो इसे सुसंगत कहा जाता है; अन्यथा, इसे असंगत माना जाता है।

5. दो चर में रेखीय समीकरणों को हल करने की डिटरमिनेंट विधि

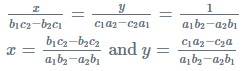
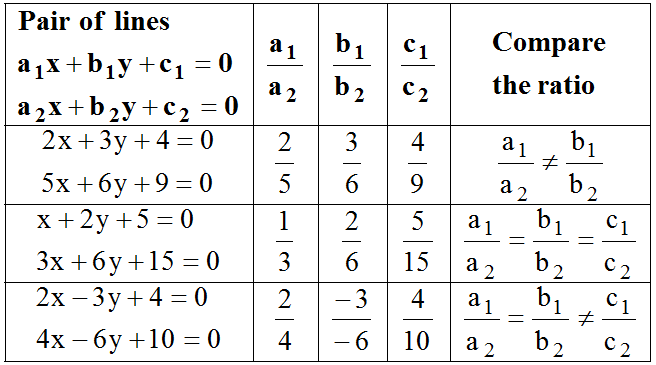
इस विधि के अंतर्गत, हम दो चर वाले रेखीय समीकरणों के एक प्रणाली के समाधान का निर्धारण करना सीखेंगे। इसके चरण इस प्रकार हैं:

• चरण 1: प्रश्नों को इस प्रकार मानें: a1x + b1y = c1 और a2x + b2y = c2
• चरण 2: सबसे पहले, हम x और y के गुणांक द्वारा विकसित की गई निर्धारण को खोजेंगे और इसे Δ के रूप में चिह्नित करेंगे।
• चरण 3: इसके बाद हम Δx का निर्धारण प्राप्त करेंगे, जो कि Δ के पहले स्तंभ को समीकरण में स्थिरांक के साथ प्रतिस्थापित करके गणना की गई निर्धारण है।
• चरण 4: इसी तरह हम Δy का निर्धारण करेंगे, जिसे Δ के दूसरे स्तंभ को समीकरण में स्थिरांक के साथ प्रतिस्थापित करके गणना किया जाता है।
• चरण 5: अंत में, दिए गए रेखीय समीकरणों के प्रणाली का समाधान निम्नलिखित सूत्रों द्वारा प्राप्त होता है:

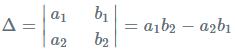
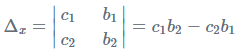
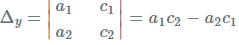
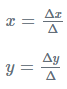
तीन चर वाले समीकरण

• मान लें कि समीकरण इस प्रकार हैं: a1x + b1y + c1z = d1, a2x + b2y + c2z = d2 और a3x + b3y + c3z = d3। यहाँ हम निम्नलिखित मैट्रिसिस को परिभाषित करते हैं:
• यदि Determinant of D ≠ 0, तो समीकरणों का एक अद्वितीय समाधान है।
• यदि Determinant of D = 0, और कम से कम एक लेकिन सभी Dx, Dy या Dz में से कोई एक शून्य है, तो कोई समाधान नहीं है।
• यदि Determinant of D = 0, और तीनों Dx, Dy और Dz शून्य हैं, तो अनंत समाधान हैं।
• निर्धारण की गणना इस प्रकार की जा सकती है: D = a1(b2c3 - c2b3) - b1(a2c3 - c2a3) + c1(a2b3 - b2a3)

तीन चर वाले समीकरणों को हल करना

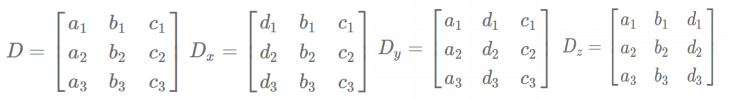
चरण 1: दिए गए तीन समीकरणों में से किसी भी दो समीकरण को लें और इसे एक चर के लिए हल करें। फिर से दो समीकरण लें और इसे ऊपर के समान चर के लिए हल करें। अब दो समीकरणों को हल करें और उनके मान ज्ञात करें, और मान को किसी भी तीन समीकरण में डालें। उदाहरण के लिए,

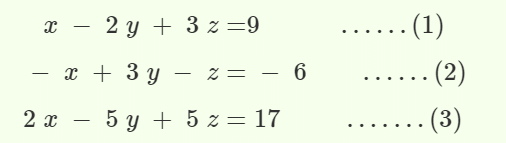
चरण 2: x को समाप्त करने के लिए समीकरण (1) और (2) को जोड़ें।

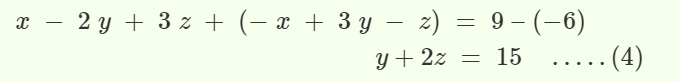
चरण 3: समीकरण 1 और 3 को हल करें, समीकरण (1) को -2 से गुणा करके और समीकरण (3) में जोड़कर।

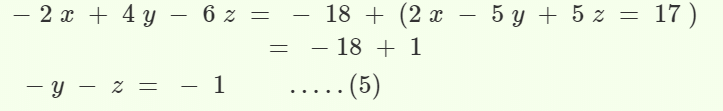
चरण 4: समीकरण 4 और 5 को हल करें।

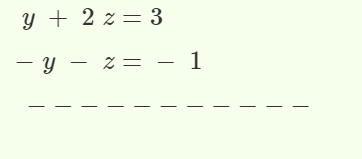
z = 2, x = 1, y = -1। इसलिए, दिए गए तीन समीकरणों का समाधान (1, -1, 2) है। इस प्रकार, हम तीन चर के साथ रेखीय समीकरण हल कर सकते हैं।

हल किए गए उदाहरण

प्रश्न 1: कुछ वास्तविक संख्याओं a और b के लिए, समीकरणों का समूह x और y के लिए бесконечно कई समाधान रखता है। तब, ab का अधिकतम संभव मान है: (a) 33 (b) 25 (c) 15 (d) 55 उत्तर: (a) समाधान: यह दिया गया है कि कुछ वास्तविक संख्याओं a और b के लिए, समीकरणों का समूह

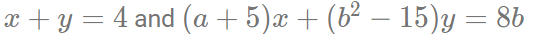
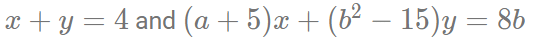
8b के लिए x और y के लिए бесконечно कई समाधान हैं। इसलिए, हम कह सकते हैं कि

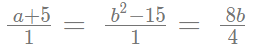
यह समीकरण a और b का मान ज्ञात करने के लिए उपयोग किया जा सकता है। सबसे पहले, हम b का मान निर्धारित करेंगे।

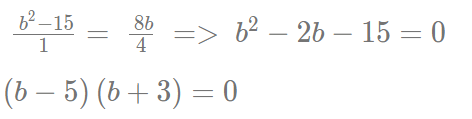
इसलिए, b के मान 5 और -3 हैं। a का मान b के संदर्भ में व्यक्त किया जा सकता है, जो है

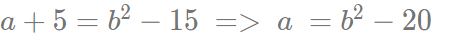
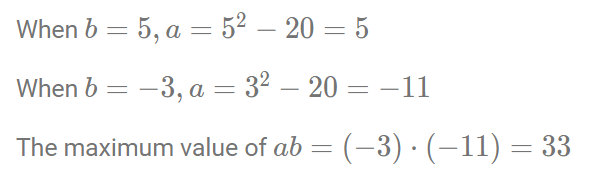
सही विकल्प A है।

प्रश्न 2: तीन दोस्त, जो फिल्म से लौट रहे थे, एक रेस्टोरेंट में खाना खाने के लिए रुके। रात के खाने के बाद, उन्होंने अपना बिल चुकाया और सामने की काउंटर पर एक चॉकलेट की कटोरी देखी। सीता ने चॉकलेट का एक तिहाई लिया, लेकिन चार वापस कर दिए क्योंकि उसे एक क्षणिक अपराधबोध हुआ। फातिमा ने फिर से बचे हुए में से एक चौथाई लिया लेकिन इसी कारण से तीन वापस कर दिए। ईस्वरी ने फिर से शेष में से आधा लिया लेकिन दो वापस कटोरी में फेंक दिए। जब यह सब खत्म हुआ, तब कटोरी में केवल 17 चॉकलेट बचे थे। कटोरी में मूल रूप से कितनी चॉकलेट थीं? (a) 38 (b) 31 (c) 41 (d) इनमें से कोई नहीं उत्तर (D) समाधान: मान लीजिए कि कटोरी में चॉकलेट की कुल संख्या n है। सीता ने n/3 - 4 लिया। शेष = 2n/3 + 4। फातिमा ने 1/4(2n/3 + 4) - 3 लिया। शेष = 3/4(2n/3 + 4) + 3। ईस्वरी ने 1/2(3/4(2n/3 + 4) + 3) - 2 लिया। शेष = 1/2(3/4(2n/3 + 4) + 3) + 2 = 17 => 3/4(2n/3 + 4) + 3 = 30 => (2n/3 + 4) = 36 => n = 48। इसलिए, उत्तर विकल्प d है।

प्रश्न 3: 2010 में, एक पुस्तकालय में दो श्रेणियों - कथा और गैर-कथा में कुल 11500 पुस्तकें थीं। 2015 में, पुस्तकालय में इन दो श्रेणियों में कुल 12760 पुस्तकें थीं। इस अवधि के दौरान, कथा श्रेणी में 10% की वृद्धि हुई जबकि गैर-कथा श्रेणी में 12% की वृद्धि हुई। 2015 में पुस्तकालय में कितनी कथा पुस्तकें थीं? (क) 6160 (ख) 6600 (ग) 6000 (घ) 5500 उत्तर (ख) समाधान: मान लें कि 2010 में कथा और गैर-कथा पुस्तकों की संख्या क्रमशः 100a और 100b है। यह दिया गया है कि 2010 में पुस्तकों की कुल संख्या = 11500 है। 100a + 100b = 11500 ——-सम Eq 1 2015 में कथा और गैर-कथा पुस्तकों की संख्या = 110a और 112b है। 110a + 112b = 12760 ——-सम Eq 2 इन दोनों समीकरणों को हल करने पर हमें b = 55 और a = 60 मिलता है। 2015 में कथा पुस्तकों की संख्या = 110 * 60 = 6600