टिप्स और ट्रिक्स: रेखीय समीकरण | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download

परिभाषा

एक रेखीय समीकरण एक गणितीय अभिव्यक्ति है जो द्विआयामी कार्टेशियन समन्वय प्रणाली में एक सीधी रेखा से संबंधित होती है। इसका रूप y=mx + b होता है, जहाँ x और y चर का प्रतिनिधित्व करते हैं, m रेखा की ढाल को दर्शाता है, और b y-प्रतिच्छेदन को संकेत करता है।

रेखीय समीकरण के टिप्स और ट्रिक्स और शॉर्टकट्स

• इस गाइड में, हम प्रतिस्पर्धी परीक्षाओं और विभिन्न भर्ती आकलनों में रेखीय समीकरण प्रश्नों को प्रभावी ढंग से हल करने के लिए त्वरित और सरल टिप्स और ट्रिक्स प्रस्तुत करते हैं, जिसका उद्देश्य आपके प्रदर्शन में सुधार करना है।
• गलत विकल्पों को समाप्त करना इन समस्याओं को हल करने का एक व्यावहारिक दृष्टिकोण है। इसमें दिए गए मानों को समीकरण में प्रतिस्थापित करना और उस विकल्प की पहचान करना शामिल है जो इसे संतुष्ट करता है।
• रेखीय समीकरण सामान्यतः मानक रूप y= mx + b का पालन करते हैं। परीक्षाओं में इस रूप से संबंधित दो प्रकार के प्रश्न अक्सर होते हैं, जैसा कि नीचे समझाया गया है।

रेखीय समीकरण हल करने के शॉर्टकट्स

रेखीय समीकरणों को तेजी से और प्रभावी ढंग से हल करने के लिए कई शॉर्टकट्स और तकनीकें हैं। यहाँ कुछ उपयोगी शॉर्टकट्स हैं:

• समान तत्वों को मिलाना: हल करने से पहले, समीकरण को सरल बनाएं और दोनों पक्षों पर समान तत्वों को मिलाएं।
• चर को पृथक करना: समीकरण के एक पक्ष पर चर (आमतौर पर x) को रखने की दिशा में काम करें, इसके लिए विपरीत क्रियाओं (जोड़, घटाव, गुणा, भाग) का उपयोग करें ताकि सभी अन्य तत्व विपरीत पक्ष पर चले जाएं।
• भिन्नात्मक रूप का उपयोग करना: जब समीकरण में भिन्न शामिल होते हैं, तो भिन्नात्मक रूप में समीकरण के साथ काम करना अक्सर अधिक प्रबंधनीय होता है, जिससे बड़े संख्याओं से निपटना आसान हो जाता है।
• रद्दीकरण: यदि समीकरण के दोनों पक्षों पर समान कारक वाले तत्व हैं, तो आप उन्हें रद्द कर सकते हैं ताकि समीकरण को सरल बनाया जा सके।
• भिन्नों को समाप्त करने के लिए गुणा करें: भिन्नों को हटाने के लिए, पूरे समीकरण को हर एक भाजक का सबसे छोटा समापवर्तक (LCM) से गुणा करें।
• क्रॉस-मल्टिप्लिकेशन: अनुपात या भिन्नों वाले समीकरणों में, चर को सरल बनाने और हल करने के लिए क्रॉस-मल्टिप्लिकेशन का उपयोग करें।

इन त्वरित विधियों और रणनीतियों का उपयोग न केवल समय बचाता है बल्कि रेखीय समीकरणों को हल करने में आपकी दक्षता को भी बढ़ाता है। फिर भी, यह महत्वपूर्ण है कि प्रत्येक शॉर्टकट के पीछे के सिद्धांतों को समझे रखें ताकि आपके समाधानों की सटीकता बनी रहे।

प्रकार 1: रेखीय समीकरणों के लिए x या y का मान खोजने के शॉर्टकट।

उदाहरण 1: यदि 3a + 6 = 4a − 2, तो a का मान क्या है? (a) 3 (b) 8 (c) 6 (d) 7 उत्तर: (b)

हल:

• 3a + 6 = 4a − 2
• 6 + 2 = 4a - 3a
• 8 = a

उदाहरण 2: निम्नलिखित में से कौन-सी समीकरण (2, 5) और (4, 11) बिंदुओं के माध्यम से गुजरने वाली रेखा की सही समीकरण है? (a) y = 3x - 1 (b) y = 2x + 1 (c) y = 2x + 3 (d) y = 3x + 5 उत्तर: (a)

हल: दो दिए गए बिंदुओं के माध्यम से गुजरने वाली रेखा की समीकरण खोजने के लिए, हम पहले ढलान (m) की गणना करते हैं:

बिंदुओं (2, 5) और (4, 11) के लिए, ढलान है:

इसके बाद, हम रेखीय समीकरण का बिंदु-ढलान रूप का उपयोग करते हैं: y – y1 = m(x – x1)

मूल्य (2, 5) और m = 3 को डालने पर, हमें समीकरण मिलता है: y – 5 = 3(x – 2)। y के लिए हल करने पर, हमें मिलता है: y = 3x - 1।

प्रकार 2: रेखीय प्रश्नों के लिए टिप्स और ट्रिक्स (शब्द समस्याएँ)

उदाहरण 1: 5 कंबल और 6 बेडशीट की कीमत ₹1500 है। 6 कंबल और 5 बेडशीट की कीमत ₹1300 है। एक कंबल और एक बेडशीट की कुल लागत खोजें। (a) ₹255 (b) ₹250 (c) ₹81.81 (d) ₹254.545 उत्तर: (d)

हल:

• मान लें कि कंबल की लागत x है और बेडशीट की लागत y है। प्रश्न के अनुसार:
• 5x + 6y = 1500…(1)
• 6x + 5y = 1300…(2)
• समीकरण 1 को 5 से और समीकरण 2 को 6 से गुणा करें, हमें मिलता है:
• 25x + 30y = 7500…(3)
• 36x + 30y = 7800…(4)
• समीकरण (3) को समीकरण (4) से घटाते हैं:
• 11x = 300
• x = 300/11
• y = 2500/11
• कुल लागत = x + y = 2800/11 = 254.545

उदाहरण 2: समीकरण 2x + 3y = 12 द्वारा प्रदर्शित रेखा का x-इंटरसेप्ट क्या है? (a) 4 (b) 6 (c) 8 (d) 12 उत्तर: (b)

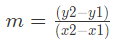
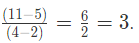
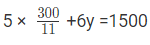
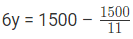
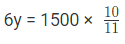
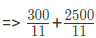
हल: (2x 3y) / 12 = 12 / 12 ⇒ (2x / 12) (3y / 12) = 1 ⇒ (x / 6) (y / 4) = 1 जो कि एक रेखा के इंटरसेप्ट रूप में है। x-intercept 6 है, और y-intercept 4 है।

उदाहरण 3: यदि रेखा 3x – y = 5 रेखा 2x + ky = 8 के समानांतर है, तो k का मान क्या होगा? (a) -3/2 (b) -2/3 (c) 2/5 (d) 3/5 उत्तर: (b)

हल: दो रेखाएँ समानांतर होती हैं यदि उनके ढलान समान होते हैं। रेखा 3x – y = 5 का ढलान ढलान-इंटरसेप्ट रूप (y = mx + b) में समीकरण को पुनर्व्यवस्थित करके पाया जा सकता है, जहाँ m ढलान है। इसलिए, 3x – y = 5 को y = 3x – 5 में बदलते हैं, और ढलान 3 है। रेखा 2x + ky = 8 को भी y = -(2/k)x + 8/k के रूप में पुनर्व्यवस्थित किया जा सकता है, जहाँ ढलान -2/k है। दोनों ढलानों (3 और -2/k) को समान करने के लिए, हमें -2/k = 3 बनाना होगा। k के लिए हल करने पर, हमें k = -2/3 मिलता है।