हल किए गए उदाहरण: रैखिक समीकरण | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download

रेखीय समीकरण की परिभाषा

रेखीय समीकरण एक गणितीय अभिव्यक्ति है जो दो-आयामी कार्टेशियन समन्वय प्रणाली में एक सीधी रेखा को दर्शाती है। यह समीकरण सामान्यतः y = mx + b के रूप में प्रस्तुत किया जाता है।

रेखीय समीकरण हल करने के लिए टिप्स

यहाँ कुछ उपयोगी टिप्स दिए गए हैं जो आपको रेखीय समीकरणों को प्रभावी रूप से हल करने में मदद करेंगे:

• चर को अलग करें: उद्देश्य यह है कि चर (आमतौर पर 'x' के रूप में दर्शाया जाता है) को समीकरण के एक पक्ष में ले जाएँ। अन्य सभी पदों को विपरीत पक्ष में ले जाने के लिए विपरीत संचालन (जोड़, घटाव, गुणा, भाग) का उपयोग करें।
• समान पदों को मिलाएँ: यदि एक ही पक्ष पर कई पद हैं, तो उन्हें मिलाकर समीकरण को सरल बनाएं।
• वितरण गुण का उपयोग करें: जब आप कोष्ठकों का सामना करते हैं, तो उनके भीतर के पदों को वितरित करें ताकि कोष्ठक समाप्त हो जाएं।
• भिन्नों को समाप्त करें: यदि समीकरण में भिन्न हैं, तो उन्हें समाप्त करने के लिए दोनों पक्षों को सामान्य हर के साथ गुणा करें।
• समीकरण का संतुलन बनाए रखें: समीकरण के दोनों पक्षों पर एक ही संचालन करके समानता सुनिश्चित करें।
• गुणनखंडों को सरल बनाएं: यदि वर्गमूल या अन्य गुणनखंड हैं, तो उन्हें सही वर्ग के गुणांक पहचानकर सरल बनाने का प्रयास करें।
• ऋणात्मक संख्याओं का ध्यान रखें: ऋणात्मक चिह्नों पर ध्यान दें और गणना के दौरान चिह्न की त्रुटियों से बचें।
• अपने समाधान की पुष्टि करें: चर के मान को निर्धारित करने के बाद, इसे मूल समीकरण में वापस डालें ताकि इसकी संतोषजनकता की पुष्टि हो सके।
• नियमित अभ्यास करें: किसी भी कौशल की तरह, रेखीय समीकरणों में प्रवीणता के लिए नियमित अभ्यास आवश्यक है। विभिन्न समस्याओं को हल करें ताकि दक्षता बढ़ सके।
• सामान्य गलतियों से सीखें: रेखीय समीकरण हल करते समय छात्रों द्वारा की जाने वाली सामान्य गलतियों को पहचानें और उनसे बचें।
• ग्राफिकल प्रतिनिधित्व: कभी-कभी, समीकरण को समन्वय तल पर ग्राफ करने से समाधान को दृश्यात्मक रूप में समझने में मदद मिलती है।
• शब्द समस्याओं को हल करें: शब्द समस्याओं को रेखीय समीकरणों में परिवर्तित करें, चर को परिभाषित करें और समाधान शुरू करने से पहले समीकरण स्थापित करें।

रेखीय समीकरण प्रश्नों और उत्तरों के नियम

• यदि a=b है, तो a+c=b+c किसी भी c के लिए। इसका अर्थ है कि हम समीकरण के दोनों पक्षों में एक संख्या c जोड़ सकते हैं और समीकरण नहीं बदलेगा।
• यदि a=b है, तो a−c=b−c किसी भी c के लिए। पिछली विशेषता की तरह, हम समीकरण के दोनों पक्षों से एक संख्या c घटा सकते हैं।
• यदि a=b है, तो ac=bc किसी भी c के लिए। जोड़ने और घटाने की तरह, हम समीकरण के दोनों पक्षों को एक संख्या c से गुणा कर सकते हैं, बिना समीकरण को बदले।
• यदि a=b है, तो a/c=b/c किसी भी गैर-शून्य c के लिए। हम समीकरण के दोनों पक्षों को एक गैर-शून्य संख्या c से विभाजित कर सकते हैं, बिना समीकरण को बदले।

उदाहरण

उदाहरण 1: समीकरण 4x − 3 × 2x² 32 = 0 के जड़ें शामिल होंगी- (a) 20 (b) 40 (c) 5 (d) 17 उतर: (d) 4x−3×2x² 32=0 4x−6x 34=0 −2x 34=0 2x−34=0 2x=34 x=17

उदाहरण 2: यदि x = 1 2^1/2 और y=1-2^1/2, तो x² y² है - (a) 107/2 (b) 203/2 (c) 997/2 (d) 445/2 उतर: (d) x = 1 2^1/2 और y=1-2^1/2 x² y² = 2 441/2 = 445/2

उदाहरण 3: 2x y=2 और 2x - y = 21/2, x का मान है: (a) 10/14 (b) 9/8 (c) 25/8 (d) 5/4 उतर: (c) 2x y = 2 2x - y = 21/2 दोनों समीकरणों को जोड़ने पर हमें मिलता है: 4x = 25/2 x = 25/8

उदाहरण 4: समीकरण 3y + 4x=12 द्वारा दर्शाई गई रेखा की ढलान क्या है? (a) 3/4 (b) −4/3 (c) 3 (d) −4 उतर: (b) रेखा की ढलान ज्ञात करने के लिए, हमें समीकरण को ढलान-इंटरसेप्ट रूप में पुनः लिखना होगा (y=mx + b), जहाँ m ढलान है। y के लिए हल करने पर हमें मिलता है। x का गुणांक ढलान का प्रतिनिधित्व करता है, इसलिए सही उत्तर है −4/3

उदाहरण 5: यदि 6(x-3) = 36(x-5), तो x का मान क्या है? (a) 51/5 (b) 27/5 (c) 15/7 (d) 17/3 उतर: (b) 6(x-3) = 36(x-5) x - 3 = 6(x - 5) x - 3 = 6x - 30 5x = 27 x = 27/5

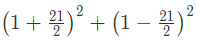
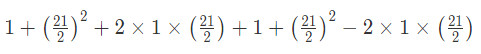
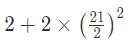
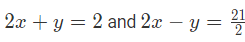
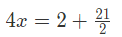
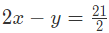
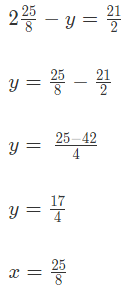
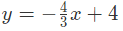
उदाहरण 6: यदि ax = b, by = c और cz = a हैं, तो xyz का मान क्या होगा: (a) 4 (b) 3 (c) 2 (d) 1 उत्तर: (d) ax = b, by = c और cz = a x = b/a, y = c/b, z = a/c, xyz = 1

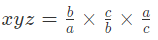
उदाहरण 7: यदि 4x³ = 2x⁷ है, तो x का मान क्या होगा: (a) 2 (b) 3 (c) 1 (d) 4 उत्तर: (a) 4x³ = 2x⁷ 2x = 4, x = 2

उदाहरण 8: यदि x = 8, y = 27, तो (a) (b) (c) (d) का मान क्या होगा? उत्तर: (b)

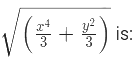
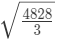
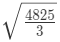
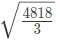
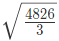
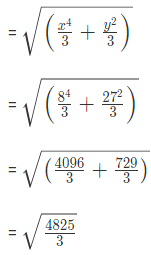
उदाहरण 9: यदि 2x + 3y = 16 और 2x - 3y = 36 है, तो x का मान क्या होगा: (a) 13 (b) 23 (c) 33 (d) 43 उत्तर: (a) 2x + 3y = 16 -----(1) 2x - 3y = 36 ------ (2) दोनों समीकरणों को जोड़ने पर हमें 4x = 52 मिलता है, x = 13

उदाहरण 10: निर्धारित करें कि क्या क्रमबद्ध त्रय (3,−2,1) प्रणाली का समाधान है: 2x + y + z = 5, 6x−4y + 5z = 31, 5x + 2y + 2z = 13 (a) सच (b) झूठ (c) कोई समाधान नहीं (d) उपरोक्त में से कोई नहीं उत्तर: (a) हम हर समीकरण की जाँच करेंगे, क्रमबद्ध त्रय के लिए x, y, और z के मान डालकर: x + y + z = 2(3) + (−2) + (1) = 5, सच 6x−4y + 5z = 6(3)−4(−2) + 5(1) = 18 + 8 = 31, सच 5x + 2y + 2z = 5(3) + 2(−2) + 2(1) = 15−4 + 2 = 13, सच। क्रमबद्ध त्रय (3,−2,1) वास्तव में प्रणाली का समाधान है।