टिप्स और ट्रिक्स: द्विघात समीकरण | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download

क्वाड्रेटिक समीकरण के प्रश्नों को हल करने के लिए टिप्स और शॉर्टकट्स

जड़ियों के संकेत को ढूंढने के लिए हम समीकरण में दिए गए संकेत का उपयोग करते हैं।

उदाहरण के लिए: x² + 3x – 4 = 0। इसके फैक्टर्स 4 और 1 हैं। अब हम जड़ियों के संकेत को खोजेंगे। तालिका के अनुसार, यदि समीकरण में दिया गया संकेत + और - है, तो उनकी जड़ियों का संकेत - और + होगा। इसलिए, समीकरण की जड़ियाँ -4 और 1 हैं।

प्रकार 1: क्वाड्रेटिक प्रश्नों के लिए ट्रिक्स और शॉर्टकट्स

जब एक समीकरण की जड़ें सकारात्मक होती हैं जबकि दूसरे की नकारात्मक होती हैं, या जब दोनों समीकरणों की जड़ें समान संकेत की होती हैं, तो जड़ों की तुलना करके उनके बीच के संबंध को निर्धारित करें।

प्रश्न 1: निम्नलिखित समीकरण को हल करके नीचे दिए गए सही विकल्प को खोजें: x² – 7x + 10 = 0 और y² + 8y + 15 = 0। (a) x < y="" (b)="" x="" /> y (c) x ≤ y (d) x ≥ y उत्तर: (b) x² – 7x + 10 = 0.... (1) पहले समीकरण की जड़ें 5 और 2 हैं। ऊपर दी गई तालिका का उपयोग करके हम जड़ों के संकेत को खोजेंगे। यदि समीकरण में दिया गया संकेत - है, तो उनकी जड़ियों का संकेत + और + होगा। इसलिए, समीकरण की जड़ियाँ 5 और 2 हैं। अब, y² + 8y + 15 = 0 .... (2) दूसरे समीकरण की जड़ें 3 और 5 हैं। यदि समीकरण में दिया गया संकेत + है, तो उनकी जड़ियों का संकेत - और - होगा। इसलिए, समीकरण की जड़ियाँ -3 और -5 हैं। अब, यहाँ जड़ें x₁, x₂, -y₁, और -y₂ हैं। यह स्पष्ट रूप से दिखाता है कि X की जड़ें सकारात्मक हैं और Y की जड़ें नकारात्मक हैं। इसलिए, x > y।

प्रकार 2: क्वाड्रेटिक समीकरण प्रश्नों को हल करने के लिए टिप्स और ट्रिक्स

जब समीकरण की जड़ें सकारात्मक और नकारात्मक होती हैं और हम उनके बीच संबंध नहीं खोज पाते।

Q2: निम्नलिखित समीकरण को हल करके सही विकल्प खोजें: 6x² + 11x – 35 = 0 और 6y² + 5y – 6 = 0। (a) x < y="" (b)="" x="" /> y (c) x ≤ y (d) निर्धारित नहीं किया जा सकता। उत्तर: (d) 6x² + 11x – 35 = 0…. (1) पहले समीकरण की जड़ों के मान 3.5 और 1.66 हैं। उपरोक्त तालिका का उपयोग करते हुए, हम जड़ों के चिन्ह का पता लगाएंगे। यदि समीकरण में चिन्ह + और – दिया गया है, तो उनकी जड़ों का चिन्ह – होगा। इसलिए, समीकरण की जड़ें हैं – 3.5 और 1.66। अब, 6y² + 5y – 6 = 0 ……. (2) दूसरे समीकरण की जड़ों के मान 1.5 और 0.66 हैं। यदि समीकरण में चिन्ह + और – दिया गया है, तो उनकी जड़ों का चिन्ह – होगा। इसलिए, समीकरण की जड़ें हैं – 1.5 और 0.66। अब, यहाँ जड़ें हैं -x₁, x₂, – y₁, और y₂। इसका अर्थ है x₂ > – y₁ और –x₁ < />₂। इसलिए, हम यह निर्धारित नहीं कर सकते कि कौन सी जड़ें बड़ी हैं।

Type 3: द्विघात प्रश्नों के लिए सुझाव, तकनीक और शॉर्टकट

जब हम एक समीकरण पा सकते हैं जहाँ x एक चर है और a, b, और c स्थिरांक का प्रतिनिधित्व करते हैं और D, अर्थात् डिस्क्रिमिनेंट। डिस्क्रिमिनेंट द्विघात सूत्र का वह भाग है जो वर्गमूल चिन्ह के नीचे होता है: b² - 4ac।

Q3: निम्नलिखित समीकरण का डिस्क्रिमिनेंट और जड़ें खोजें: 3x² − 5x − 7 = 0। समाधान: चलिए डिस्क्रिमिनेंट निकालते हैं, D = 109। तो दो जड़ें हैं 2.57 और -0.90।

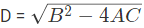
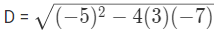
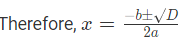
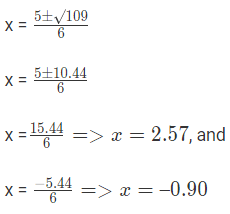
Q4: उस विधि का नाम बताएं जिसका उपयोग उन द्विघात समीकरणों को हल करने के लिए किया जाता है जिन्हें आसानी से विभाजित नहीं किया जा सकता या जिनमें जटिल गुणांक शामिल होते हैं? (a) फैक्टरिंग (b) द्विघात सूत्र (c) स्क्वायर पूरा करना (d) अनुमान। उत्तर: (b) द्विघात सूत्र एक सार्वभौमिक विधि है जिसका उपयोग किसी भी द्विघात समीकरण को हल करने के लिए किया जाता है, चाहे उसके गुणांक या विभाजन की क्षमता कुछ भी हो। यह सीधे जड़ों की गणना करके सटीक समाधान प्रदान करता है।

प्रश्न 5: द्विघात समीकरण 3x² + 6x – 9 = 0 के लिए, मूल (roots) क्या हैं?
(क) x = 1
(ख) x = -1
(ग) x = -3
(घ) x = 3
उत्तर: (ग) समीकरण को सरल बनाने के लिए पूरे समीकरण को 3 से बाँट दें: x² + 2x – 3 = 0। इस समीकरण को (x – 1)(x + 3) के रूप में गुणनखंडित (factor) किया जा सकता है। प्रत्येक गुणनखंड को शून्य (zero) के बराबर रखते हुए, हमें x – 1 = 0 और x + 3 = 0 प्राप्त होता है। दोनों समीकरणों को हल करने से हमें x = 1 और x = -3 मिलते हैं। इसलिए, मूल हैं x = -3 और x = 1।