हल किए गए उदाहरण: द्विघात समीकरण | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download

क्वाड्रेटिक समीकरण की परिभाषा

एक क्वाड्रेटिक समीकरण का रूप ax² + bx + c = 0 होता है, जो एक दूसरे दर्जे के बहुपद समीकरण का प्रतिनिधित्व करता है, जहाँ 'a', 'b', और 'c' स्थिरांक होते हैं, और 'x' चर है। इसे एक वास्तविक क्वाड्रेटिक समीकरण मानने के लिए 'a' का शून्य से भिन्न होना आवश्यक है।

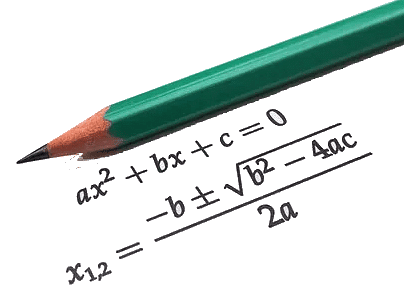
क्वाड्रेटिक समीकरण के मूल निकालने की विधियाँ

एक क्वाड्रेटिक समीकरण के मूल या समाधान वे 'x' के मान होते हैं जो समीकरण को सत्य बनाते हैं। एक क्वाड्रेटिक समीकरण में दो वास्तविक मूल, दो जटिल मूल, या एक वास्तविक मूल (पूर्ण वर्ग के मामले में) हो सकते हैं। मूलों की संख्या डिस्क्रिमिनेंट (Δ) के मान द्वारा निर्धारित होती है, जिसे निम्नलिखित रूप में व्यक्त किया जाता है:

Δ = b² − 4ac

• यदि Δ > 0, तो क्वाड्रेटिक समीकरण के दो भिन्न वास्तविक मूल होते हैं।
• यदि Δ = 0, तो क्वाड्रेटिक समीकरण का एक वास्तविक मूल (दोहराए गए या समान मूल) होता है।
• यदि Δ < 0,="" तो="" क्वाड्रेटिक="" समीकरण="" के="" दो="" जटिल="" मूल="" (संयोगात्मक="" जोड़े)="" होते="" />

क्वाड्रेटिक समीकरण के मूल खोजने के लिए कई विधियाँ उपयोग की जा सकती हैं:

• फैक्टरिंग: यदि समीकरण को फैक्टर किया जा सके, तो मूल सीधे फैक्टर्स से निर्धारित किए जा सकते हैं।
• क्वाड्रेटिक फॉर्मूला: क्वाड्रेटिक फॉर्मूला किसी भी क्वाड्रेटिक समीकरण के मूल खोजने की एक सामान्य विधि है और इसे इस प्रकार व्यक्त किया जाता है: जहाँ ± चिह्न दो संभावित समाधानों को दर्शाता है।
• स्क्वायर पूरा करना: इस विधि में क्वाड्रेटिक समीकरण को पूर्ण वर्ग के रूप में परिवर्तित किया जाता है, जिससे मूल आसानी से प्राप्त किए जा सकते हैं।

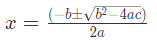
क्वाड्रेटिक समीकरण के नियम

यदि p √q किसी द्विघात समीकरण की जड़ है, तो इसकी दूसरी जड़ p-√q है।

• यदि p √q किसी द्विघात समीकरण की जड़ है, तो इसकी दूसरी जड़ p-√q है।
• जब D ≥ 0 होता है, तो rx² dx z को दो रेखीय गुणनखंडों के रूप में व्यक्त किया जा सकता है।
• यदि α और β rx² dx z के जड़ हैं, तो हम इसे इस रूप में लिख सकते हैं: x² – (α β)x + α β = 0।

उदाहरण

उदाहरण 1: यदि x² - 3x + 1 = 0, तो x 1/x का मान ज्ञात करें। (a) 0 (b) 3 (c) 2 (d) 1 उत्तर: (b) दी गई समीकरण है x² - 3x + 1 = 0 ⇒ x² + 1 = 3x ⇒ x² 1/x = 3 ⇒ x²/x 1/x = 3 ∴ x 1/x = 3

उदाहरण 2: k के लिए किस मान पर समीकरण x² + 2(k - 4)x + 2k = 0 में समान जड़ें हैं? (a) 6 और 4 (b) 8 और 2 (c) 10 और 4 (d) 12 और 2 उत्तर: (b) दी गई समीकरण है x² + 2(k - 4)x + 2k = 0। यहाँ, a = 1, b = 2(k - 4), c = 2k। चूंकि, जड़ें समान हैं, हमें D = 0 होना चाहिए।

• b² - 4ac = 0
• 4(k - 4)² - 8k = 0
• 4(k² - 16 - 8k) - 8k = 0
• ⇒ 4k² - 64 - 32k - 8k = 0
• ⇒ 4k² - 40k + 64 = 0
• ⇒ k² - 10k + 16 = 0
• ⇒ k² - 8k - 2k + 16 = 0
• ⇒ k(k - 8) - 2(k - 8) = 0
• ⇒ (k - 8)(k - 2) = 0

उदाहरण 3: यदि α और β समीकरण 4x² - 19x + 12 = 0 के जड़ हैं, तो 1/α और 1/β के जड़ों वाला समीकरण ज्ञात करें। (a) 4x² + 19 + 12 = 0 (b) 12x² - 19x + 4 = 0 (c) 12x² + 19x + 4 = 0 (d) 4x² - 19x - 12 = 0 उत्तर: (b) दी गई समीकरण है 4x² - 19x + 12 = 0। मान लें कि दी गई समीकरण के जड़ 1/α और 1/β हैं। तब आवश्यक समीकरण है 12x² - 19x + 4 = 0।

उदाहरण 4: यदि द्विघात समीकरण 7y² - 50y + k = 0 की एक जड़ 7 है, तो k का मान क्या होगा? (a) 7 (b) 1 (c) 50/7 (d) 7/50 उत्तर: (a) दी गई द्विघात समीकरण 7y² - 50y + k = 0 है। यदि एक जड़ 7 है, तो यह समीकरण को संतुष्ट करेगा, अर्थात् y = 7 को समीकरण में डालने पर: 7 × (7)² - 50 × 7 + k = 0 ⇒ 7 × 49 - 350 + k = 0 ⇒ 343 - 350 + k = 0 ∴ k = 7

उदाहरण 5: वह द्विघात समीकरण जिसकी जड़ें 3 और -1 हैं, है (a) x² - 4x + 3 = 0 (b) x² - 2x - 3 = 0 (c) x² + 2x - 3 = 0 (d) x² + 4x + 3 = 0 उत्तर: (b) यह दिया गया है कि, द्विघात समीकरण की जड़ें 3 और -1 हैं। मान लीजिए α = 3 और β = -1। जड़ों का योग = α + β = 3 - 1 = 2। जड़ों का गुणनफल = α × β = (3) × (-1) = -3। ∴ आवश्यक द्विघात समीकरण है x² - (α + β)x + αβ = 0 ⇒ x² - (2)x - 3 = 0 ⇒ x² - 2x - 3 = 0